广东省茂名市高州校际联盟2021-2022学年七年级下学期期中考试数学试题（B卷）

试卷更新日期：2022-04-29 类型：期中考试

进入出卷网下载

一、单选题

1. 计算 $a^{3} \cdot a^{3}$ 正确的结果是（）

A、 $a^{6}$ B、 $2 a^{3}$ C、 $a^{9}$ D、 $a^{27}$

查看试题解析
2. 新冠病毒的直径为0.000000125米，这个数据用科学记数法表示为（）

A、 $1.25 \times 1 0^{- 10}$ B、 $1.25 \times 1 0^{- 11}$ C、 $1.25 \times 1 0^{- 8}$ D、 $1.25 \times 1 0^{- 7}$

查看试题解析
3. 下面四个图形中， $∠ 1$ 与 $∠ 2$ 是对顶角的图形是（）

A、 B、 C、 D、

查看试题解析
4. 若∠ $α$ ＝42°，则∠ $α$ 的补角的大小是（）

A、138° B、148° C、48° D、58°

查看试题解析
5. 计算 $202 2^{0}$ 的结果是（）

A、1 B、0 C、2022 D、 $\frac{1}{2022}$

查看试题解析
6. 如图，直线 $a$ ， $b$ 被第三条直线 $c$ 所截．由“ $∠ 1 = ∠ 2$ ”，得到“ $a ∥ b$ ”的依据是（）

A、两直线平行，同位角相等 B、同位角相等，两直线平行 C、两直线平行，内错角相等 D、内错角相等，两直线平行

查看试题解析
7. 小苏现已存款180元．为赞助“希望工程”，她计划今后每月存款10元，则存款总金额 $y$ （元）与时间 $x$ （月）之间的关系式是（）

A、 $y = 10 x$ B、 $y = 180 x$ C、 $y = 180 - 10 x$ D、 $y = 180 + 10 x$

查看试题解析
8. 如图，直线 $a ∥ b$ ，直角 $Δ A B C$ 的直角顶点 $C$ 在直线 $b$ 上，若 $∠ 1 = 50 °$ ，则 $∠ 2$ 的度数为（）

A、 $60 °$ B、 $50 °$ C、 $40 °$ D、 $30 °$

查看试题解析
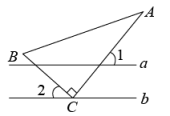9. 在课外实验活动中，一位同学以固定的速度向某一容器中注水，若水深h（cm）与时间t（s）之间的关系的图象大致如图所示，则这个容器是下列图中的（）

A、 B、 C、 D、

查看试题解析
10. 若 $x^{2} + k x + 64$ 为一个完全平方式，则 $k$ 的值为（）

A、16 B、 $\pm 16$ C、8 D、 $\pm 8$

查看试题解析

二、填空题

11. 计算 $- (2 a^{2} b)^{3} =$ ．

查看试题解析
12. 计算： $(x^{4} - 4 x^{3}) \div x^{2} =$ ．

查看试题解析
13. 如图，直线a、b被c所截， $∠ 1 = 130 °$ ，当 $∠ 2 =$ °时， $a ∥ b$

查看试题解析
14. 一根蜡烛燃烧过程中，剩余蜡烛长y（厘米）和燃烧时间x（小时）的关系如图所示，则这根蜡烛燃烧4小时，剩余蜡烛长为厘米．

查看试题解析
15. 若 $2^{m} = 3$ ， $2^{n} = 6$ ， $(m$ ， $n$ 为正数），则 $2^{m + n} =$ ．

查看试题解析
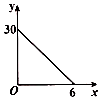16. 高州市出租车的收费标准是：不超过 $2 k m$ 收4元，超过 $2 k m$ 后，每千米收1元．设行车路程为 $x k m$ ，收费为 $y$ （元），则 $y$ 与 $x$ （ $x > 2$ ）的关系式为．

查看试题解析
17. 将一张长方形纸条 $A B C D$ 沿 $E F$ 折叠，点 $B$ ， $A$ 分别落在 $B^{'}$ ， $A^{'}$ 位置上， $F B^{'}$ 与 $A D$ 的交点为 $G$ ．若 $∠ D G F = 110 °$ ，则 $∠ F E G$ 的度数为 $°$ ．

查看试题解析

三、解答题

18. 计算：

(1)、 $a^{3} \cdot a^{3} + (2 a^{3})^{2} - 2 a^{6}$ ；

(2)、 $(π - 3)^{0} + (\frac{1}{2})^{- 2} + (- 1)^{2022}$ ．

查看试题解析
19. 如图， $∠ E A D = 130 °$ ， $∠ B = 50 °$ ，试说明 $E F ∥ B C$ ．

查看试题解析
20. 先化简，再求值： $(x + y) (x - y) + y (x + 2 y)$ ，其中 $x = 2$ ， $y = 1$ ．

查看试题解析
21. 用简便方法计算下列各题：

(1)、 $9 9^{2}$ ；

(2)、 $10 2^{2} - 101 \times 103$ ．

查看试题解析
22. 小明骑单车上学，当他骑了一段路时，想起要买某本书，于是又折回到刚经过的新华书店，买到书后继续去学校．以下是他本次上学所用的时间与路程的关系图，根据图中提供的信息回答下列问题：

(1)、小明家到学校的路程是米，他在书店停留了分钟；

(2)、本次上学途中，小明一共骑行了米，一共用了分钟；

(3)、我们认为骑单车的速度超过300米 $/$ 分就超过了安全限度．请求出整个上学途中各个时间段小明的骑车速度，哪个时间段的速度不在安全限度内？

查看试题解析
23. 请补全下面的证明：
如图，已知∠1＝∠2，∠C＝∠D，求证：DF∥AC．
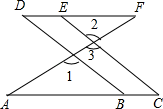
解：∵∠1＝∠2（              ）
∠2＝∠3（              ）
∴∠1＝∠3（等量代换）
∴BD∥                  ▲                  （              ）
∴∠C＝∠DBA（              ）
又∵∠C＝∠D（              ）
∴∠DBA＝                  ▲                  （等量代换），
∴DF∥AC（              ）

查看试题解析
24.

(1)、计算并观察下列各式填空：
$(x - 1) (x + 1) =$ $x^{2} - 1$ ；
$(x - 1) (x^{2} + x + 1) =$ $x^{3} - 1$ ；
$(x - 1) (x^{3} + x^{2} + x + 1) =$ ；

(2)、从上面的算式及计算结果，你发现了什么？请根据你发现的规律直接填写下面的空格：
$(x - 1)$ （） $= x^{6} - 1$ ；

(3)、利用你发现的规律计算： $(x - 1) (x^{7} + x^{6} + x^{5} + x^{4} + x^{3} + x^{2} + x + 1) =$ ；

(4)、利用该规律计算： $1 + 2 + 2^{2} + 2^{3} + \dots + 2^{2021}$ 的值．

查看试题解析
25.

(1)、（问题）如图1，若 $A B ∥ C D$ ， $∠ A E P = 40 °$ ， $∠ P F C = 50 °$ ，求 $∠ E P F$ 的度数．

(2)、（问题迁移）如图2， $A B ∥ C D$ ，点 $P$ 在 $A B$ 的上方，问 $∠ P E A$ ， $∠ P F C$ ， $∠ E P F$ 之间有何数量关系？请说明理由；

(3)、（联想拓展）如图3所示，在（2）的条件下，已知 $∠ E P F = 60 °$ ， $∠ P F C = 120 °$ ， $∠ P E A$ 的平分线和 $∠ P F C$ 的平分线交于点 $G$ ，直接写出 $∠ G$ 的度数．

查看试题解析