广东省茂名市高州校际联盟2021-2022学年八年级下学期期中考试数学试题(B卷)
试卷更新日期:2022-04-29 类型:期中考试
一、单选题
-
1. 等腰三角形的两条边长分别为8和4,则它的周长等于( )A、12 B、16 C、20 D、16或202. 已知直角三角形中30°角所对的直角边为2cm,则斜边的长为( )A、1cm B、2cm C、4cm D、8cm3. 判断两个直角三角形全等的方法错误的有( )A、两条直角边对应相等 B、斜边和一锐角对应相等 C、斜边和一条直角边对应相等 D、两个锐角对应相等4. 已知不等式的解集在数轴上表示如图所示,则此不等式的解集是( )
 A、 B、 C、 D、5.
A、 B、 C、 D、5.如图,地面上有三个洞口A、B、C , 老鼠可以从任意一个洞口跑出,猫为能同时最省力地顾及到三个洞口(到A、B、C三个点的距离相等),尽快抓到老鼠,应该蹲守在( )
 A、△ABC三边垂直平分线的交点 B、△ABC三条角平分线的交点 C、△ABC三条高所在直线的交点 D、△ABC三条中线的交点6. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
A、△ABC三边垂直平分线的交点 B、△ABC三条角平分线的交点 C、△ABC三条高所在直线的交点 D、△ABC三条中线的交点6. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 下列从左到右的变形,是分解因式的是( )A、 B、 C、 D、8. 如图,沿直角边BC所在的直线向右平移得到 , 下列结论中错误的是( )
7. 下列从左到右的变形,是分解因式的是( )A、 B、 C、 D、8. 如图,沿直角边BC所在的直线向右平移得到 , 下列结论中错误的是( )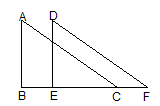 A、≌ B、 C、 D、9.
A、≌ B、 C、 D、9.直线y=kx+b与两坐标轴的交点如图所示,当y<0时,x的取值范围是 ( )
 A、x>2 B、x<2 C、x>-1 D、x<-110. 如图,△ABC是等边三角形,AQ=PQ , PR⊥AB于点R , PS⊥AC于点S , PR=PS.下列结论:①点P在∠A的角平分线上;②AS=AR;③QP∥AR;④△BRP≌△QSP . 其中,正确的有( )
A、x>2 B、x<2 C、x>-1 D、x<-110. 如图,△ABC是等边三角形,AQ=PQ , PR⊥AB于点R , PS⊥AC于点S , PR=PS.下列结论:①点P在∠A的角平分线上;②AS=AR;③QP∥AR;④△BRP≌△QSP . 其中,正确的有( )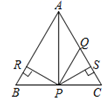 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
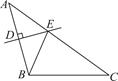
11. 已知 , , 则的值为 .12. 已知一个三角形的三边长a、b、c,满足(a-b)2+|b-c|=0,则这个三角形是 三角形。13. 在平面直角坐标系中,若点 在第二象限,则 的取值范围为 .14. 如图,在△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为 .
 15. 不等式组 的解集为 .16. 如图,将线段AB平移到线段CD的位置,则a+b的值为 .
15. 不等式组 的解集为 .16. 如图,将线段AB平移到线段CD的位置,则a+b的值为 .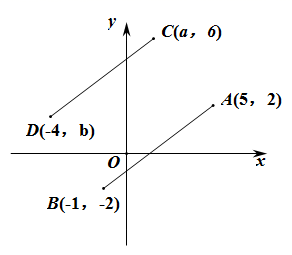 17. 如图,Rt△ABC的两直角边AB,BC长分别为6,8,其三条角平分线交于点O,将△ABC分为三个三角形,则S△ABO:S△BCO :S△CAO = .
17. 如图,Rt△ABC的两直角边AB,BC长分别为6,8,其三条角平分线交于点O,将△ABC分为三个三角形,则S△ABO:S△BCO :S△CAO = .
三、解答题
-
18. 解不等式:≤1并把解集在数轴上表示出来.19. 因式分解(1)、2a3b3+3a2b2-ab;(2)、5x²(y+4)-15x(y+4),20. 如图,△ABC的直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,求PP′的长.
 21. 在边长为1的小正方形网格中,△AOB的顶点均在格点上.
21. 在边长为1的小正方形网格中,△AOB的顶点均在格点上. (1)、将△AOB向左平移3个单位长度,再向上平移1个单位长度得到△ , 请画出△ , 并写出点的坐标;(2)、将△AOB绕点O沿顺时针方向旋转90°得到△ , 请画出△ , 并写出点的坐标.22. 如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A、B两点的距离相等.
(1)、将△AOB向左平移3个单位长度,再向上平移1个单位长度得到△ , 请画出△ , 并写出点的坐标;(2)、将△AOB绕点O沿顺时针方向旋转90°得到△ , 请画出△ , 并写出点的坐标.22. 如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A、B两点的距离相等.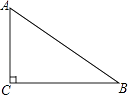 (1)、用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);(2)、连结AD,若∠B=32°,求∠CAD的度数.23. 甲、乙两家旅行社为了吸引更多的顾客,分别推出赴某地旅游的团体(多于4人)优惠办法.甲旅行社的优惠办法是:买4张全票,其余人按半价优惠;乙旅行社的优惠办法是:所有人都打七五折优惠.已知这两家旅行社的原价均为每人1000元,那么随着团体人数的变化,哪家旅行社的收费更优惠.24. 已知,如图,在△ABC中,AB=AC,∠BAC=120°,AP⊥BC,垂足为D,且AP=AB.
(1)、用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);(2)、连结AD,若∠B=32°,求∠CAD的度数.23. 甲、乙两家旅行社为了吸引更多的顾客,分别推出赴某地旅游的团体(多于4人)优惠办法.甲旅行社的优惠办法是:买4张全票,其余人按半价优惠;乙旅行社的优惠办法是:所有人都打七五折优惠.已知这两家旅行社的原价均为每人1000元,那么随着团体人数的变化,哪家旅行社的收费更优惠.24. 已知,如图,在△ABC中,AB=AC,∠BAC=120°,AP⊥BC,垂足为D,且AP=AB. (1)、求证:△ABP是等边三角形;(2)、若E是边AB上一点,∠EPF=60°,PF交AC于点F,试判断BE与AF的数量关系,并说明理由.25. 某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)、求每台A型电脑和B型电脑的销售利润各多少元?(2)、该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑a台,这100台电脑的销售总利润为w元.
(1)、求证:△ABP是等边三角形;(2)、若E是边AB上一点,∠EPF=60°,PF交AC于点F,试判断BE与AF的数量关系,并说明理由.25. 某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)、求每台A型电脑和B型电脑的销售利润各多少元?(2)、该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑a台,这100台电脑的销售总利润为w元.①求关于a的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?