安徽省安庆市2021-2022学年七年级下学期期中数学试题
试卷更新日期:2022-04-29 类型:期中考试
一、单选题
-
1. 下列各数没有平方根的是( )A、0 B、 C、 D、2. 在实数 , 0, , π,中,无理数有( )A、1个 B、2个 C、3个 D、4个3. 估计68的立方根的大小在( )
A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间4. 若 , 则下列各式不成立的是( )A、 B、 C、 D、5. 不等式组的解集在数轴上表示,正确的是( )A、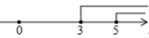 B、
B、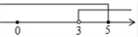 C、
C、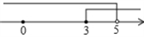 D、
D、 6. 下列计算正确的是( )A、 B、 C、 D、7. 四个小朋友玩跷跷板,他们的体重分别为P、Q、R、S , 如图所示,则他们的体重大小关系是( )
6. 下列计算正确的是( )A、 B、 C、 D、7. 四个小朋友玩跷跷板,他们的体重分别为P、Q、R、S , 如图所示,则他们的体重大小关系是( ) A、P>R>S>Q B、Q>S>P>R C、S>P>Q>R D、S>P>R>Q8. 已知 , , 则等于( )A、 B、 C、 D、29. 将 , , 这三个数按从小到大的顺序排列,正确的结果是( )A、 < < B、 < < C、 < < D、 < <10. 如果不等式组有解,则的取值范围是( )A、 B、 C、 D、
A、P>R>S>Q B、Q>S>P>R C、S>P>Q>R D、S>P>R>Q8. 已知 , , 则等于( )A、 B、 C、 D、29. 将 , , 这三个数按从小到大的顺序排列,正确的结果是( )A、 < < B、 < < C、 < < D、 < <10. 如果不等式组有解,则的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 扫描隧道显微镜发明后,世界上便诞生了一门新学科,就是“纳米技术”已知52个纳米的长度为0.000000052米,用科学记数法表示这个数为米12. 若 ,则(a+b)m的值为 .13. 一个正数的两个平方根分别是和 , 则这个正数是 .14. 当时,的解是非正数.
三、解答题
-
15. 计算: .16. 解不等式组 , 并在数轴上表示不等式组的解集.17. 已知 , 求的值.18. 已知是算术平方根,是的立方根,求的值.19. 在实数范围内定义一种新运算“★”其运算规则为 , .(1)、若 , 则 .(2)、求不等式的负整数解.20. 观察下列一组等式:(1)、以上这些等式中,你有何发现?利用你的发现填空.
① ▲ ;
②( );
③( ) .
(2)、利用你发现的规律来计算: .21. 阅读:我们知道,于是要解不等式 , 我们可以分两种情况去掉绝对值符号,转化为我们熟悉的不等式,按上述思路,我们有以下解法:解:⑴当 , 即时:
解这个不等式,得:
由条件 , 有:
⑵当 , 即时,
解这个不等式,得:
由条件 , 有:

∴如图,综合(1)、(2)原不等式的解为
根据以上思想,请探究完成下列2个小题:
(1)、;(2)、 .22. 如图所示,回答下列问题. (1)、大正方形的面积是多少?(2)、梯形Ⅱ,Ⅲ的面积 , 分别是多少?(3)、试求与的值;(4)、由(3)你发现了什么?请用含 , 的式子表示你的结论.23. 为了保护环境,某化工厂一期工程完成后购买了3台甲型和2台乙型污水处理设备,共花费资金54万元,且每台乙型设备的价格是每台甲型设备价格的75%,实际运行中发现,每台甲型设备每月能处理污水200吨,每台乙型设备每月能处理污水160吨,且每年用于每台甲型设备的各种维护费和电费为1万元,每年用于每台乙型设备的各种维护费和电费为1.5万元.今年该厂二期工程即将完成,产生的污水将大大增加,于是该厂决定再购买甲、乙两型设备共8台用于二期工程的污水处理,预算本次购买资金不超过84万元,预计二期工程完成后每月将产生不少于1300吨污水.
(1)、大正方形的面积是多少?(2)、梯形Ⅱ,Ⅲ的面积 , 分别是多少?(3)、试求与的值;(4)、由(3)你发现了什么?请用含 , 的式子表示你的结论.23. 为了保护环境,某化工厂一期工程完成后购买了3台甲型和2台乙型污水处理设备,共花费资金54万元,且每台乙型设备的价格是每台甲型设备价格的75%,实际运行中发现,每台甲型设备每月能处理污水200吨,每台乙型设备每月能处理污水160吨,且每年用于每台甲型设备的各种维护费和电费为1万元,每年用于每台乙型设备的各种维护费和电费为1.5万元.今年该厂二期工程即将完成,产生的污水将大大增加,于是该厂决定再购买甲、乙两型设备共8台用于二期工程的污水处理,预算本次购买资金不超过84万元,预计二期工程完成后每月将产生不少于1300吨污水.
(1)、请你计算每台甲型设备和每台乙型设备的价格各是多少元?(2)、请你求出用于二期工程的污水处理设备的所有购买方案;(3)、若两种设备的使用年限都为10年,请你说明在(2)的所有方案中,哪种购买方案的总费用最少?(总费用=设备购买费+各种维护费和电费)