人教版数学九年级复习专题8 四边形
试卷更新日期:2022-04-28 类型:三轮冲刺
一、单选题
-
1. 平行四边形一定具有的性质是( )A、内角和为180° B、是中心对称图形 C、邻边相等 D、对角互补2. 如图,△ABC中,E是AB的中点,过点E作ED∥BC,交AC于点D,则△AED与四边形BCDE的面积比是( )
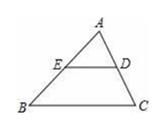 A、1:1 B、1:2 C、1:3 D、1:43. 顺次连接矩形的各边中点,所得的四边形一定是( )A、正方形 B、菱形 C、矩形 D、梯形4. 如图,将边长为的正方形绕点B逆时针旋转30°,那么图中阴影部分的面积为( )
A、1:1 B、1:2 C、1:3 D、1:43. 顺次连接矩形的各边中点,所得的四边形一定是( )A、正方形 B、菱形 C、矩形 D、梯形4. 如图,将边长为的正方形绕点B逆时针旋转30°,那么图中阴影部分的面积为( ) A、3 B、 C、 D、5. 如图,在平面直角坐标系中,平行四边形OABC的顶点 , 点A在x轴的正半轴上,∠COA的平分线OD交BC于点 , 则点C的坐标为( )
A、3 B、 C、 D、5. 如图,在平面直角坐标系中,平行四边形OABC的顶点 , 点A在x轴的正半轴上,∠COA的平分线OD交BC于点 , 则点C的坐标为( )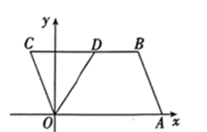 A、 B、 C、 D、6. 如图,菱形ABCD的对角线AC,BD相交于点O,E为DC的中点,若OE=2,则菱形的周长为 ( )
A、 B、 C、 D、6. 如图,菱形ABCD的对角线AC,BD相交于点O,E为DC的中点,若OE=2,则菱形的周长为 ( )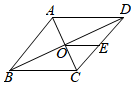 A、10 B、12 C、16 D、207. 如图,菱形ABCD中,AE=1,AF=BE=2.若P为对角线BD 上一动点,则EP+FP的最小值为( )
A、10 B、12 C、16 D、207. 如图,菱形ABCD中,AE=1,AF=BE=2.若P为对角线BD 上一动点,则EP+FP的最小值为( )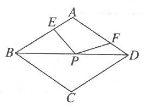 A、1 B、2 C、3 D、48. 一个四边形要成为矩形,需要的条件是( )A、两个内角相等 B、三个内角相等 C、四个内角相等 D、两个外角为直角9. 下列命题是真命题的是( )A、对角线互相平分的四边形是平行四边形 B、对角线相等的四边形是矩形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直平分的四边形是正方形10. 如图,在平面直角坐标系中,菱形 的边 在x轴的正半轴上,反比例函数 的图象经过对角线 的中点D和顶点C若菱形 的面积为9,则k的值为( )
A、1 B、2 C、3 D、48. 一个四边形要成为矩形,需要的条件是( )A、两个内角相等 B、三个内角相等 C、四个内角相等 D、两个外角为直角9. 下列命题是真命题的是( )A、对角线互相平分的四边形是平行四边形 B、对角线相等的四边形是矩形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直平分的四边形是正方形10. 如图,在平面直角坐标系中,菱形 的边 在x轴的正半轴上,反比例函数 的图象经过对角线 的中点D和顶点C若菱形 的面积为9,则k的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E.若AB=6cm,AD=9cm,则EC=cm.
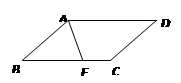 12. 如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上OA=5;OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.则D坐标为.
12. 如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上OA=5;OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.则D坐标为.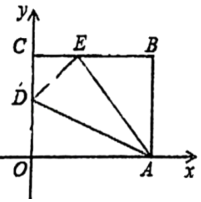 13. 如图,在矩形ABCD中,AB=8,BC=6,点P为边AB上任意一点,过点P作PE⊥AC,PF⊥BD,垂足分别为E、F,则PE+PF=.
13. 如图,在矩形ABCD中,AB=8,BC=6,点P为边AB上任意一点,过点P作PE⊥AC,PF⊥BD,垂足分别为E、F,则PE+PF=.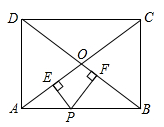 14. 如图.点E在正方形ABCD的边BC上,2BE=3CE,过点D作AE的垂线交AB于F,点G为垂足,若FG=3,则EG的长为 .
14. 如图.点E在正方形ABCD的边BC上,2BE=3CE,过点D作AE的垂线交AB于F,点G为垂足,若FG=3,则EG的长为 . 15. 如图,一个正方形摆放在桌面上,那么这个正方形的边长为 .
15. 如图,一个正方形摆放在桌面上,那么这个正方形的边长为 . 16. 如图,在平面直角坐标系中,点A1(1,0)、A2(3,0)、A3(6,0)、A4(10,0)、……,以A1A2为对角线作第一个正方形A1C1A2B1 , 以A2A3为对角线作第二个正方形A2C2A3B2 , 以A3A4 , 为对角线作第三个正方形A3C3A4B3 , ……,顶点B1 , B2 , B3……都在第一象限,按照此规律依次下去,则点Bn的坐标为.
16. 如图,在平面直角坐标系中,点A1(1,0)、A2(3,0)、A3(6,0)、A4(10,0)、……,以A1A2为对角线作第一个正方形A1C1A2B1 , 以A2A3为对角线作第二个正方形A2C2A3B2 , 以A3A4 , 为对角线作第三个正方形A3C3A4B3 , ……,顶点B1 , B2 , B3……都在第一象限,按照此规律依次下去,则点Bn的坐标为.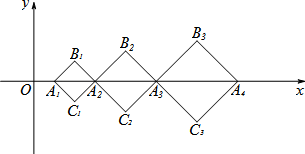
三、解答题
-
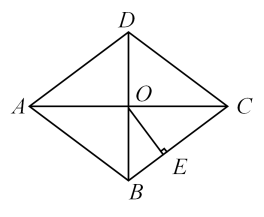
17. 如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,求OE的长.
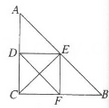
 18. 如图所示,在△ABC中,D,E,F分别是AC,AB,BC的中点,且CE= AB.
18. 如图所示,在△ABC中,D,E,F分别是AC,AB,BC的中点,且CE= AB.求证:四边形CFED是矩形.
 19. 已知:在菱形 中,点E,O,F分别为AB,AC,AD的中点,连接 , .求证: ;
19. 已知:在菱形 中,点E,O,F分别为AB,AC,AD的中点,连接 , .求证: ; 20. 如图,在矩形ABCD中,AB=20cm,动点P从点A开始沿AB边以4cm/s的速度运动,动点Q从点C开始沿CD边以1cm/s的速度运动.点P和点Q同时出发,当其中一点到达终点时,另一点也随之停止运动,设动点的运动时间为ts,则当t为何值时,四边形APQD是矩形?
20. 如图,在矩形ABCD中,AB=20cm,动点P从点A开始沿AB边以4cm/s的速度运动,动点Q从点C开始沿CD边以1cm/s的速度运动.点P和点Q同时出发,当其中一点到达终点时,另一点也随之停止运动,设动点的运动时间为ts,则当t为何值时,四边形APQD是矩形?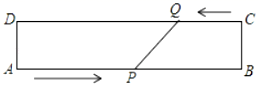 21. 放缩尺是一种绘图工具,它能把图形放大或缩小.
21. 放缩尺是一种绘图工具,它能把图形放大或缩小.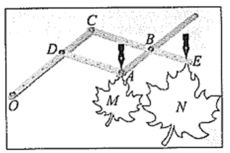
制作:把钻有若干等距小孔的四根直尺用螺栓分别在点A,B,C,D处连接起来,使得直尺可以绕着这些点转动,O为固定点, , , 在点A,E处分别装上画笔.
画图:现有一图形M,画图时固定点O,控制点A处的笔尖沿图形M的轮廓线移动,此时点E处的画笔便画出了将图形M放大后的图形N.
原理:
连接 , , 可证得以下结论:
①和为等腰三角形,则 , (180°-∠ ▲ );
②四边形为平行四边形(理由是 ▲ );
③ , 于是可得O,A,E三点在一条直线上;
④当时,图形N是以点O为位似中心,把图形M放大为原来的 ▲ 倍得到的.