人教版数学九年级复习专题6 二次函数及其应用
试卷更新日期:2022-04-28 类型:三轮冲刺
一、单选题
-
1. 抛物线y=(x﹣1)2﹣2的顶点坐标为( )A、(1,2) B、(1,﹣2) C、(﹣1,2) D、(﹣1,﹣2)2. 在平面直角坐标系中,将抛物线y=x2向上平移2个单位长度,再向右平移1个单位长度,得到的抛物线的解析式是( )A、y=(x﹣1)2+2 B、y=(x﹣1)2﹣2 C、y=(x+1)2﹣2 D、y=(x+1)2+23. 二次函数y=(x-3)2+1的最小值是( )A、3 B、-3 C、1 D、-14. 已知二次函数 (其中m>0),下列说法正确的是( )A、当x>2时,都有y随着x的增大而增大 B、当x<3时,都有y随着x的增大而减小 C、若x<n时,都有y随着x的增大而减小,则 D、若x<n时,都有y随着x的增大而减小,则5. 若A(﹣6,y1),B(﹣3,y2),C(1,y3)为二次函数y=2x2﹣1图象上的三点,则y3 , y2 , y1的大小关系是( )A、y3<y2<y1 B、y2<y3<y1 C、y3<y1<y2 D、y2<y1<y36. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0)和B,与y轴交于点C.下列结论:
①abc<0,②2a+b>0,③4a﹣2b+c>0,④3a+c>0,其中正确的结论个数为( )
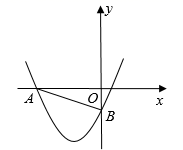
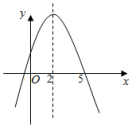
 A、1个 B、2个 C、3个 D、4个7. 若二次函数 的图象如图所示,则下列说法不正确的是( )
A、1个 B、2个 C、3个 D、4个7. 若二次函数 的图象如图所示,则下列说法不正确的是( ) A、当 时, B、当 时, 有最大值 C、图像经过点 D、当 时,8. 如图,正方形OABC的边长为2,OC与y轴正半轴的夹角为30°,点A在抛物线 的图象上,则a的值为( )
A、当 时, B、当 时, 有最大值 C、图像经过点 D、当 时,8. 如图,正方形OABC的边长为2,OC与y轴正半轴的夹角为30°,点A在抛物线 的图象上,则a的值为( )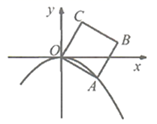 A、 B、 C、 D、9. 若二次函数的x与y的部分对应值如下表:
A、 B、 C、 D、9. 若二次函数的x与y的部分对应值如下表:x
-2
-1
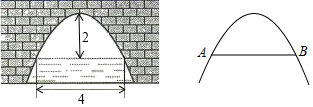
0
1
2
3
y
14
7
2
-1
-2
-1
则当时,y的值为( )
A、-1 B、2 C、7 D、1410. 在同一平面直角坐标系中,二次函数y=ax2与一次函数y=bx+c的图象如图所示,则二次函数y=ax2-bx+c的图象可能是( ) A、
A、 B、
B、 C、
C、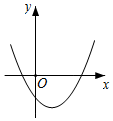 D、
D、
二、填空题
-
11. 用配方法把二次函数化成顶点式为 .12. 小强推铅球时,铅球的高度y(m)与水平行进的距离x(m)之间的关系为y(x﹣4)2+3,则小强推铅球的成绩是 m.13. 将抛物线 向左平移2个单位,再向上平移3个单位后的抛物为.14. 已知抛物线y=2x2-x-1,与 轴的一个交点为(m, 0),则代数式-4m2+2m+2022的值为.15. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则关于x的方程ax2+bx+c=0(a≠0)的解为 .
 16. 已知二次函数y=﹣x2+bx+c与一次函数y=mx+n的图象相交于点A(﹣2,4)和点B(6,﹣2),则不等式﹣x2+bx+c>mx+n的解集是 .
16. 已知二次函数y=﹣x2+bx+c与一次函数y=mx+n的图象相交于点A(﹣2,4)和点B(6,﹣2),则不等式﹣x2+bx+c>mx+n的解集是 .三、解答题
-
17. 二次函数y=ax2+bx+c的图象经过点A(4,0),B(0,﹣3),C(﹣2,0),求它的解析式,直接写出它的开口方向、对称轴和顶点坐标.18. 如图,已知抛物线 的顶点为 ,交 轴于 两点,与 轴交于点 .求线段 、 的长.
 19. 现要用60米长的篱笆围成一个矩形场地(一边靠墙且墙长40米),应怎样围才能使矩形的面积S最大?最大是多少?
19. 现要用60米长的篱笆围成一个矩形场地(一边靠墙且墙长40米),应怎样围才能使矩形的面积S最大?最大是多少?