四川省巴中市2020-2021学年高一下学期理数期末考试试卷

试卷更新日期：2022-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x > 1}$ ， $B = {x | 0 < x < 2}$ ，则 $A ∪ B =$ （）

A、 $(0 ， 2)$ B、 $(1 ， 2)$ C、 $(0 ， + ∞)$ D、 $(1 ， + \infty)$

查看试题解析
2. 若直线 $l_{1} ： 2 x + y = 0$ 与直线 $l_{2} ： x + m y + 1 = 0$ 互相平行，则实数 $m =$ （）

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、-2 D、2

查看试题解析
3. 设 $a$ ， $b$ ， $c$ 为实数且 $a > b$ ，则下列不等式一定成立的是（）

A、 $\frac{1}{a} > \frac{1}{b}$ B、 $a^{2} > b^{2}$ C、 $a c^{2} > b c^{2}$ D、 $202 1^{a - b} > 1$

查看试题解析
4. 若三点 $A (1 ， - 2)$ 、 $B (2 ， - 3)$ 、 $C (3 ， t)$ 共线，则实数 $t =$ （）

A、-4 B、-5 C、4 D、5

查看试题解析
5. 设等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，若 $a_{5} + a_{6} = a_{2} + 5$ ，则 $S_{17} =$ （）

A、5 B、17 C、85 D、170

查看试题解析
6. 在菱形 $A B C D$ 中， $A B = B D = 2$ ，若点 $E$ 为 $B C$ 中点，则 $\vec{A D} \cdot \vec{A E} =$ （）

A、2 B、1 C、 $2 + 2 \sqrt{3}$ D、6

查看试题解析
7. 在 $△ A B C$ 中，若角 $A$ 、 $B$ 、 $C$ 所对的边分别为 $a$ 、 $b$ 、 $c$ ，则下列有关正弦定理及其变形错误的是（）

A、 $a ： b ： c = s i n A ： s i n B ： s i n C$ B、 $a = b \Leftrightarrow s i n 2 A = s i n 2 B$ C、 $\frac{a}{s i n A} = \frac{b + c}{s i n B + s i n C}$ D、 $a = b \Leftrightarrow s i n A = s i n B$

查看试题解析
8. 已知 $f (x)$ 是奇函数，当 $x \geq 0$ 时， $f (x) = e^{2 x} - 1$ （其中 $e$ 为自然对数的底数），则 $f (l n \frac{1}{2}) =$ （）

A、1 B、-1 C、3 D、-3

查看试题解析
9. 已知实数 $x$ 、 $y$ 满足不等式组 ${\begin{array}{l} x - 3 y + 3 \leq 0 \\ 2 x - y + 1 \geq 0 \\ x + 2 y - 7 \leq 0 \end{array}$ ，则 $z = x - 2 y$ 的最大值为（）

A、-5 B、-2 C、-1 D、4

查看试题解析
10. 若等腰直角三角形的一条直角边所在直线的斜率为2，则斜边所在直线的斜率为（）

A、 $- \frac{1}{3}$ 或3 B、-3或 $\frac{1}{3}$ C、-4或 $\frac{1}{4}$ D、 $- \frac{4}{3}$ 或 $\frac{3}{4}$

查看试题解析
11. 声音是由物体振动产生的声波，其中纯音的数学模型是函数 $y = A s i n ω t$ ，已知函数 $f (x) = 2 c o s (2 x + φ) (- π \leq φ \leq π)$ 的图象向右平移 $\frac{π}{3}$ 个单位后，与纯音的数学模型函数 $y = 2 s i n 2 x$ 图象重合．若函数 $f (x)$ 在 $[- a ， a]$ 是减函数，则 $a$ 的最大值是（）

A、 $\frac{π}{12}$ B、 $\frac{π}{6}$ C、 $\frac{π}{3}$ D、 $\frac{π}{2}$

查看试题解析
12. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ，已知 $∠ A B C = 12 0^{∘}$ ， $∠ A B C$ 的平分线交 $A C$ 于点 $D$ ，且 $B D = 1$ ．有以下四个结论：
① $\frac{1}{a} + \frac{1}{c} = 1$ ；② $a c$ 的最小值为2；③ $a c + \frac{1}{a c}$ 的最小值为2；④ $a + 2 c + a c$ 的最小值为 $5 + 2 \sqrt{6}$ ．
其中所有正确结论的编号为（）

A、①③④ B、②④ C、①③ D、①④

查看试题解析

二、填空题

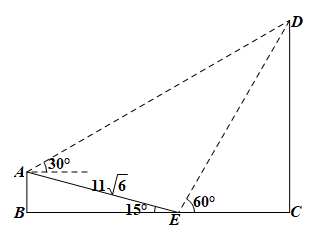
13. 已知 $f (x)$ 是以 $4$ 为周期的偶函数，且当 $x \in [0 ， 2]$ 时， $f (x) = 1 - x$ ，则 $f (- 21) =$ ．

查看试题解析
14. 已知向量 $\vec{a} = (c o s 75 ° ， s i n 75 °)$ ， $\vec{b} = (c o s 15 ° ， s i n 15 °)$ ，则 $| \vec{a} - \vec{b} | =$ ．

查看试题解析
15. 2021年5月27日，以“绿色秦巴，开放互赢”为主题的第三届秦巴山区绿色农林产业投资贸易洽谈会在四川省巴中市开幕，会场设在刚刚竣工的川东北最大的综合体育场——巴中市体育中心，即民间所说的“兴文鸟巢”，能被邀请到现场观礼是无比的荣耀．如图，在坡度为15º的观礼台上，某一列座位与旗杆在同一个垂直于地面的平面上，在该列的第一排和最后一排测得旗杆顶端的仰角分别为60º和30º，且第一排和最后一排的距离为 $11 \sqrt{6}$ 米，则旗杆的高度为米．

查看试题解析
16. 已知 $△ A B C$ 的三个内角为 $A$ ， $B$ ， $C$ ，且 $s i n A$ ， $s i n B$ ， $s i n C$ 成等差数列，则 $c o s 2 B + s i n B$ 的最大值为，最小值为．

查看试题解析

三、解答题

17. 设公差不为0的等差数列 ${a_{n}}$ 满足： $a_{3} = 6$ ，且 $a_{1}$ ， $a_{2}$ ， $a_{4}$ 成等比数列，记数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ．

(1)、求 $a_{n}$ 及 $S_{n}$ ；

(2)、令 $b_{n} = \frac{1}{S_{n}}$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ ．

查看试题解析
18. 已知关于 $x$ 的不等式 $a x^{2} + 4 a x - 3 < 0$ ．

(1)、若不等式的解集为 ${x | x < - 3$ 或 $x > - 1}$ ，求 $a$ 的值；

(2)、若不等式的解集是 $R$ ，求 $a$ 的取值范围．

查看试题解析
19. 已知数列 ${a_{n}}$ 满足 $a_{1} = 3$ ， $a_{n + 1} = 2 a_{n} - n + 1$ ，令 $b_{n} = a_{n} - n$ ．

(1)、证明：数列 ${b_{n}}$ 是等比数列；

(2)、求数列 ${a_{n}}$ 的前 $n$ 项和 $S_{n}$ ．

查看试题解析
20. 已知函数 $f (x) = 2 s i n (ω x + φ) (ω > 0 ， - \frac{π}{2} < φ < \frac{π}{2})$ 的部分图象如图所示．

(1)、求函数 $f (x)$ 的解析式；

(2)、在锐角 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ，若 $f (A) = \sqrt{3}$ ， $b = 2$ ，且 $△ A B C$ 的面积为 $\frac{3 \sqrt{3}}{2}$ ，求 $a$ ．

查看试题解析
21. 在 $△ A B C$ 中，a，b，c分别是角A，B，C的对边，且 $2 a c o s C - b c o s C = c c o s B$ .

(1)、求角C；

(2)、若 $a + b = 2$ ，求c的取值范围.

查看试题解析
22. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ 满足： $S_{1} = 4$ ， $S_{n + 1} = 2 a_{n + 1} + 2$ ．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若数列 ${b_{n}}$ 满足 $a_{n} b_{n} = l o g_{2} a_{n}$ ．
①求数列 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ ；
②若 $b_{n} \leq \frac{1}{4} m^{2} + m - \frac{3}{4}$ 对于一切正整数 $n$ 恒成立，求实数 $m$ 的取值范围．

查看试题解析