上海市普陀区2020-2021学年七年级下学期期末数学试题
试卷更新日期:2022-04-28 类型:期末考试
一、单选题
-
1. 下列实数中,无理数是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 =﹣6 B、 C、 =±2 D、2 ×3 =53. 如图,已知与相交于点O, , 从下列条件中补充一个条件,不一定能判定的是( )
 A、 B、 C、 D、4. 如图,已知 , 下列条件中不能判断直线的是( ).
A、 B、 C、 D、4. 如图,已知 , 下列条件中不能判断直线的是( ). A、 B、 C、 D、5. 直角平坐标面内,如果点在第四象限,那么点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 下列条件中,不能判断是等边三角形的是( ).A、 , B、 , C、 D、
A、 B、 C、 D、5. 直角平坐标面内,如果点在第四象限,那么点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 下列条件中,不能判断是等边三角形的是( ).A、 , B、 , C、 D、二、填空题
-
7. 16的四次方根是8. 比较大小:﹣3﹣2(填“<”或“>”).9. 近似数0.06030有个有效数字10. 已知一个三角形的两边长分别是2和5,如果它的第三边长是奇数,那么第三边的长等于 .11. 如图, , , , 那么°
 12. 经过点且垂直于x轴的直线可表示为直线13. 如图,已知OA=OB,点C在OA上,点D在OB上,OC=OD,AD与BC相交于点E,那么图中全等的三角形共有对.
12. 经过点且垂直于x轴的直线可表示为直线13. 如图,已知OA=OB,点C在OA上,点D在OB上,OC=OD,AD与BC相交于点E,那么图中全等的三角形共有对. 14. 若△ABC中,∠A:∠B:∠C=2:3:4,则△ABC是 三角形.(填:锐角或直角或钝角)15. 已知等腰三角形一腰上的高与底边的夹角是 , 那么这个等腰三角形顶角的度数是16. 在平面直角坐标系中,将点A先向右平移4个单位,再向下平移6个单位得到点B,如果点A和点B关于原点对称,那么点A的坐标是 .17. 如图,、分别是的一个内角的平分线与一个外角的平分线,过点作 , 分别交、于点E、F.如果四边形的周长是16, , 那么
14. 若△ABC中,∠A:∠B:∠C=2:3:4,则△ABC是 三角形.(填:锐角或直角或钝角)15. 已知等腰三角形一腰上的高与底边的夹角是 , 那么这个等腰三角形顶角的度数是16. 在平面直角坐标系中,将点A先向右平移4个单位,再向下平移6个单位得到点B,如果点A和点B关于原点对称,那么点A的坐标是 .17. 如图,、分别是的一个内角的平分线与一个外角的平分线,过点作 , 分别交、于点E、F.如果四边形的周长是16, , 那么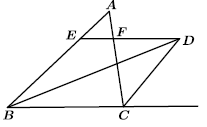 18. 在中, , D为的中点,如图所示,E为上一点,将沿着直线翻折,点B的对应点落在的延长线上,分别联结、 , 与交于点F.如果 , 那么(结果用用整数比比表示)
18. 在中, , D为的中点,如图所示,E为上一点,将沿着直线翻折,点B的对应点落在的延长线上,分别联结、 , 与交于点F.如果 , 那么(结果用用整数比比表示)
三、解答题
-
19. 计算:20. 运用幂的性质计算:21. 如图,已知 , , 试说明的理由

解:因为(已知),
所以 ▲ ( ).
因为(已知),
所以 ▲ (等量代换)
所以( ).
所以( ).
22. 如图,已知 , , , 试说明的理由.
解:因为(已知),
所以( ).
又因为(已知).
所以 ▲ ▲ (等式性质)
所以
在和中,
,
所以( )(完成以下说理过程)
23. 如图,已知中, , 根据下列要求画图并回答问题 (1)、画边上的高 , 过点A画直线 . (不要求写画法和结论)(2)、在(1)的图形中,如果 , 点B到直线的距离是3,点C到直线的距离是4,那么直线与间的距离等于 . (用含a的代数式表示)24. 解答下列各题(1)、小明在学习了平行线的判定方法后,会利用直尺和三角尺过直线外一点作已知直线的平行线,如图1所示,小明的作图依据是: .
(1)、画边上的高 , 过点A画直线 . (不要求写画法和结论)(2)、在(1)的图形中,如果 , 点B到直线的距离是3,点C到直线的距离是4,那么直线与间的距离等于 . (用含a的代数式表示)24. 解答下列各题(1)、小明在学习了平行线的判定方法后,会利用直尺和三角尺过直线外一点作已知直线的平行线,如图1所示,小明的作图依据是: .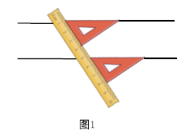
 (2)、小丽发现如果利用直尺和圆规,也可以过直线外一点作已知直线的平行线.如图2,已知直线a,点P为直线a外一点,小丽利用直尺和圆规过点P作直线平行于直线a.以下是小丽的作图方法:
(2)、小丽发现如果利用直尺和圆规,也可以过直线外一点作已知直线的平行线.如图2,已知直线a,点P为直线a外一点,小丽利用直尺和圆规过点P作直线平行于直线a.以下是小丽的作图方法:①在直线a上取一点A,作直线(与直线a不垂直);
②在的延长线上取一点B,以B为圆心长为半径作弧,交直线a于点C;
③联结 , 以B为圆心长为半径作弧,交于点D,作直线
这样,就得到直线 . 你能说明的理由吗?
25. 如图,在直角坐标平面内,点A、B、C都是格点 (1)、写出图中点A、B、C的坐标是:A , B , C .(2)、的面积是(3)、如果点P在x轴的正半轴上,且 , 那么点P的坐标是 .
(1)、写出图中点A、B、C的坐标是:A , B , C .(2)、的面积是(3)、如果点P在x轴的正半轴上,且 , 那么点P的坐标是 .

