上海市嘉定区2020-2021学年七年级下学期期末数学试题
试卷更新日期:2022-04-28 类型:期末考试
一、单选题
-
1. 下列各数,①、②0.1010010001、③、④、⑤、⑥中,其中无理数有( ).A、2个 B、3个 C、4个 D、5个2. 在数轴上表示实数 和 的点的位置如图所示,那么下列各式成立的是( )
 A、 B、 C、 D、3. 若点 在第四象限,则( )A、 , B、 , C、 , D、 ,4. 下列四个图形中,和不符合同位角定义的是( ).A、
A、 B、 C、 D、3. 若点 在第四象限,则( )A、 , B、 , C、 , D、 ,4. 下列四个图形中,和不符合同位角定义的是( ).A、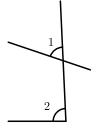 B、
B、 C、
C、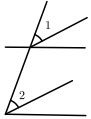 D、
D、 5. 下列说法中不正确的是( )A、有两个角及它们的夹边对应相等的两个三角形全等 B、有两个角及其中一个角的对边对应相等的两个三角形全等 C、有两条边及它们的夹角对应相等的两个三角形全等 D、有两条边及其中一条边的对角对应相等的两个三角形全等6. 如图,已知AO平分∠DAE,AD=AE,AB=AC,图中全等三角形有( ).
5. 下列说法中不正确的是( )A、有两个角及它们的夹边对应相等的两个三角形全等 B、有两个角及其中一个角的对边对应相等的两个三角形全等 C、有两条边及它们的夹角对应相等的两个三角形全等 D、有两条边及其中一条边的对角对应相等的两个三角形全等6. 如图,已知AO平分∠DAE,AD=AE,AB=AC,图中全等三角形有( ).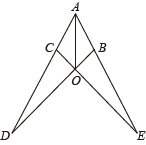 A、1对 B、2对 C、3对 D、4对
A、1对 B、2对 C、3对 D、4对二、填空题
-
7. 4的平方根是8. 若 ,则 .9. 比较大小:3.14(填“>”、“=”或“<”).10. 把表示成幂的形式是 .11. 计算: =.12. 据第7次全国人口普查统计,截止2020年11月1日零时,全国人口共141178万人,将141178这个数保留四个有效数字并用科学记数法表示是 .13. 在平面直角坐标系中,点 关于x轴对称的点的坐标是.14. 如果将点M(m,3)向左平移2个单位到达点N,这时点N恰好在y轴上,那么m的值是 .15. 如图,直线a∥b,直线c分别与a,b相交,若∠1=70°,则∠2= .
 16. 在中,如果 , 那么 .17. 已知是的角平分线,是边上一点, , 如果 , 那么 .18. 在中, , 点在边上,且满足 , , 则度.19. 如图, , 的面积为 , 那么的面积为 .
16. 在中,如果 , 那么 .17. 已知是的角平分线,是边上一点, , 如果 , 那么 .18. 在中, , 点在边上,且满足 , , 则度.19. 如图, , 的面积为 , 那么的面积为 . 20. 在平面直角坐标系中,的三个顶点分别为、、 , 如果以、、为顶点的三角形与全等(点与点不重合),请写出一个符合条件的点的坐标为 .
20. 在平面直角坐标系中,的三个顶点分别为、、 , 如果以、、为顶点的三角形与全等(点与点不重合),请写出一个符合条件的点的坐标为 .三、解答题
-
21. 计算: .22. 计算: .23. 用幂的运算性质计算:(结果表示为含幂的形式).24. 如图,已知 , , 垂足分别为点、 , , 试说明的理由.
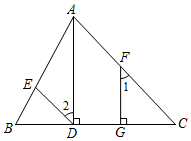
解:因为 , (已知),
所以 , ( ),
所以(等量代换),
所以( ),
所以( ),
因为(已知),
所以( ),
所以( ).
25. 如图,直角坐标平面内有 , 其中点的坐标为 , 点的坐标为 , 将绕点逆时针旋转得到 , 点、分别转到、 . (1)、在图中画出 .(2)、连接 , 求的面积.26. 如图,在△ABC中,AB=AC,点 , 在 边上, .求证: .
(1)、在图中画出 .(2)、连接 , 求的面积.26. 如图,在△ABC中,AB=AC,点 , 在 边上, .求证: .

