吉林省长春市南关区2020-2021学年七年级下学期期末数学试题
试卷更新日期:2022-04-28 类型:期末考试
一、单选题
-
1. 下列方程中,解为x=2的是( )A、2x﹣1=1 B、2x=1 C、3x﹣4=x D、3x+6=02. x=1是关于x的方程2x﹣a=0的解,则a的值是( )A、﹣2 B、2 C、﹣1 D、13. 下列等式变形中,不正确的是( )A、若a=b,则a﹣2=b﹣2 B、若am=bm,则a=b C、若a=b,则 D、若x=2,则x2=2x4. 我国明代数学读本《算法统宗》一书有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托如果1托为5尺,那么索长和竿子长分别为多少尺?设索长为x尺,竿子长为y尺,可列方程组为( )A、 B、 C、 D、5. 只用下列正多边形地砖中的一种,能够铺满地面的是( )A、正五边形 B、正六边形 C、正八边形 D、正十边形6. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 7. 不等式x+2≤3x﹣2的解集在数轴上表示正确的是( )A、
7. 不等式x+2≤3x﹣2的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 长度分别为2,7,x的三条线段能组成一个三角形,
8. 长度分别为2,7,x的三条线段能组成一个三角形, 的值可以是( ) A、4 B、5 C、6 D、99. 如图,将△ABC绕点C顺时针旋转90°得到△EDC , 若点A、D、E在同一条直线上,∠ACB=25°,在∠ADC的度数是( )
的值可以是( ) A、4 B、5 C、6 D、99. 如图,将△ABC绕点C顺时针旋转90°得到△EDC , 若点A、D、E在同一条直线上,∠ACB=25°,在∠ADC的度数是( ) A、45° B、60° C、70° D、75°10. 如图,将一张三角形纸片 的一角折叠,使点 落在 处的 处,折痕为 .如果 , , ,那么下列式子中正确的是( )
A、45° B、60° C、70° D、75°10. 如图,将一张三角形纸片 的一角折叠,使点 落在 处的 处,折痕为 .如果 , , ,那么下列式子中正确的是( )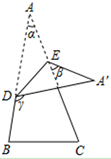 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若代数式x+1的值为﹣3,则x的值为 .12. 已知二元一次方程3x﹣2y=5,用含x的代数式表示y为 .13. 若有理数a、b满足a>b,则﹣3a﹣3b(填“>”、“<”或“=”).14. 如图,将周长为12的△ABC沿BC边向右平移3个单位,得到△DEF,则四边形ABFD的周长为 .
 15. 如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点 , AB⊥a于点B,D⊥b于点D,若OB=5,OD=3,则阴影部分的面积之和为 .
15. 如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点 , AB⊥a于点B,D⊥b于点D,若OB=5,OD=3,则阴影部分的面积之和为 . 16. 如图,在五边形ABCDE中,∠EDC与∠BCD的平分线交于点P , ∠A+∠B+∠E=280°,则∠P的度数是 .
16. 如图,在五边形ABCDE中,∠EDC与∠BCD的平分线交于点P , ∠A+∠B+∠E=280°,则∠P的度数是 . 17. 问题解决:糖葫芦一般是用竹签串上山楂.再蘸以冰糖制作而成,现将一些山楂分别串在若干个竹签上,如果每根竹签串4个山楂,还剩余3个山楂;如果每根竹签串7个山楂,还剩余6根竹签,求竹签有多少根?山楂有多少个?反思归纳:现有m根竹签,n个山楂,若每根竹签串a个山楂,还剩b个山楂,则m、n、a、b满足的等量关系为(用含m、n、a、b的代数式表示).
17. 问题解决:糖葫芦一般是用竹签串上山楂.再蘸以冰糖制作而成,现将一些山楂分别串在若干个竹签上,如果每根竹签串4个山楂,还剩余3个山楂;如果每根竹签串7个山楂,还剩余6根竹签,求竹签有多少根?山楂有多少个?反思归纳:现有m根竹签,n个山楂,若每根竹签串a个山楂,还剩b个山楂,则m、n、a、b满足的等量关系为(用含m、n、a、b的代数式表示).
三、解答题
-
18. 解方程:=1﹣ .19. 解方程组: .20. 解不等式组: , 并把解集在数轴上表示出来.
 21. 一个多边形剪去一个内角后,得到一个内角和为1980°的新多边形,求原多边形的边数.22. 如图,△ABC沿着BC的方向平移至△DEF,AC、DE交于点G,∠ACF=140°,∠B=60°,求∠D和∠DGC的度数.
21. 一个多边形剪去一个内角后,得到一个内角和为1980°的新多边形,求原多边形的边数.22. 如图,△ABC沿着BC的方向平移至△DEF,AC、DE交于点G,∠ACF=140°,∠B=60°,求∠D和∠DGC的度数. 23. 对于任意实数m、n,定义关于“⊕”的一种运算如下:m⊕n=3m﹣2n.例如:2⊕5=3×2﹣2×5=﹣4,(﹣1)⊕4=3×(﹣1)﹣2×4=﹣11(1)、若(﹣3)⊕x=2021,求x的值;(2)、若y⊕6>10,求y的最小整数解.24. 图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、B、C均在格点上,只用无刻度的直尺,在给定的网格中按要求画图.
23. 对于任意实数m、n,定义关于“⊕”的一种运算如下:m⊕n=3m﹣2n.例如:2⊕5=3×2﹣2×5=﹣4,(﹣1)⊕4=3×(﹣1)﹣2×4=﹣11(1)、若(﹣3)⊕x=2021,求x的值;(2)、若y⊕6>10,求y的最小整数解.24. 图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、B、C均在格点上,只用无刻度的直尺,在给定的网格中按要求画图. (1)、在图①中,将△ABC沿AC方向平移,当点A移动到点A1时,画出平移后的△A1B1C1;(2)、在图②中,作△ABC关于直线MN对称的△DEF,且点D、E、F均在格点上;(3)、在图③中,作△ABC关于点O成中心对称的△A2B2C225. 如图,D是△ABC的AC边上一点,∠A=∠ABD,∠BDC=150°,∠ABC=85°.求:
(1)、在图①中,将△ABC沿AC方向平移,当点A移动到点A1时,画出平移后的△A1B1C1;(2)、在图②中,作△ABC关于直线MN对称的△DEF,且点D、E、F均在格点上;(3)、在图③中,作△ABC关于点O成中心对称的△A2B2C225. 如图,D是△ABC的AC边上一点,∠A=∠ABD,∠BDC=150°,∠ABC=85°.求:⑴∠A的度数;
⑵∠C的度数.
解⑴∵∠BDC是△ABD的外角,∠BDC=150°(已知),
∴∠BDC= ▲ + ▲ ( ).
又∵∠A=∠ABD(已知),
∴∠A= ▲ 度.(等量代换).
⑵∵∠A+∠ABC+∠C= ▲ 度( ),
∴∠C=180°﹣∠ABC﹣∠A(等式性质).
又∵∠ABC=85°,
∴∠C= ▲ 度.
 26. 如图,某农场准备用80米的护栏围成一块靠墙的矩形花园,设矩形花园的长为x米,宽为y米.
26. 如图,某农场准备用80米的护栏围成一块靠墙的矩形花园,设矩形花园的长为x米,宽为y米. (1)、当y=22时,求x的值;(2)、由于受场地条件的限制,y的取值范围为16≤y≤26,求x的取值范围.27.
(1)、当y=22时,求x的值;(2)、由于受场地条件的限制,y的取值范围为16≤y≤26,求x的取值范围.27. (1)、【感知】如图①,在四边形AEFC中,EB、FD分别是边AE、CF的延长线,我们把∠BEF、∠DFE称为四边形AEFC的外角,若∠A+∠C=260°,则∠BEF+∠DFE=度.(2)、【探究】如图②,在四边形AECF中,EB、FD分别是边AE、AF的延长线,我们把∠BEC、∠DFC称为四边形AECF的外角,试探究∠A、∠C与∠BEC、∠DFC之间的数量关系.(3)、【结论】综合以上,请你用文字描述上述关系: .(4)、【应用】如图③,FM、EM分别是四边形AEFC的外角∠DFE、∠BEF的平分线,若∠A+∠C=210°,求∠M的度数.
(1)、【感知】如图①,在四边形AEFC中,EB、FD分别是边AE、CF的延长线,我们把∠BEF、∠DFE称为四边形AEFC的外角,若∠A+∠C=260°,则∠BEF+∠DFE=度.(2)、【探究】如图②,在四边形AECF中,EB、FD分别是边AE、AF的延长线,我们把∠BEC、∠DFC称为四边形AECF的外角,试探究∠A、∠C与∠BEC、∠DFC之间的数量关系.(3)、【结论】综合以上,请你用文字描述上述关系: .(4)、【应用】如图③,FM、EM分别是四边形AEFC的外角∠DFE、∠BEF的平分线,若∠A+∠C=210°,求∠M的度数.