吉林省长春市朝阳区2020-2021学年七年级下学期期末数学试题
试卷更新日期:2022-04-28 类型:期末考试
一、单选题
-
1. 方程的解是( )A、 B、 C、 D、2. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若有理数、满足> , 则下列结论正确的是( )A、 B、 C、> D、<4. 如图,张明同学设计了四种正多边形的瓷砖图案,这四种瓷砖图案中,不能铺满地面的是( )A、
3. 若有理数、满足> , 则下列结论正确的是( )A、 B、 C、> D、<4. 如图,张明同学设计了四种正多边形的瓷砖图案,这四种瓷砖图案中,不能铺满地面的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,一个倾斜的天平两边分别放有小立方体和砝码,每个砝码的质量都是5克,每个小立方体的质量都是m克,则m的取值范围为( )
5. 如图,一个倾斜的天平两边分别放有小立方体和砝码,每个砝码的质量都是5克,每个小立方体的质量都是m克,则m的取值范围为( ) A、m<15 B、m>15 C、m< D、m>6. 按如图所示的运算程序,使输出结果为1的x、y的值是( )
A、m<15 B、m>15 C、m< D、m>6. 按如图所示的运算程序,使输出结果为1的x、y的值是( ) A、 B、 C、 D、7. 如图,将四边形ABCD去掉一个60°的角得到一个五边形BCDEF,则∠1与∠2的和为( )
A、 B、 C、 D、7. 如图,将四边形ABCD去掉一个60°的角得到一个五边形BCDEF,则∠1与∠2的和为( ) A、60° B、108° C、120° D、240°8. 如图,将 绕点 按顺时针旋转 得到 ,若点 、 、 在同一条直线上, ,则 的大小为 ( )
A、60° B、108° C、120° D、240°8. 如图,将 绕点 按顺时针旋转 得到 ,若点 、 、 在同一条直线上, ,则 的大小为 ( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 已知二元一次方程 , 用含的代数式表示= .10. 不等式的正整数解为 .11. 已知 是等腰三角形,若它的周长为18,一条边的长为4,则它的腰长为 .12. 如图所示的花朵图案,至少要旋转度后,才能与原来的图形重合.
 13. 如图,点F是△ABC的边BC延长线上一点,DF⊥AB于点D,∠A=30°,∠F=40°,∠ACF的度数是 .
13. 如图,点F是△ABC的边BC延长线上一点,DF⊥AB于点D,∠A=30°,∠F=40°,∠ACF的度数是 .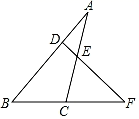 14. 如图,在 中,沿 折叠,点C落在点B处,已知 的周长是15, ,则 的周长为.
14. 如图,在 中,沿 折叠,点C落在点B处,已知 的周长是15, ,则 的周长为.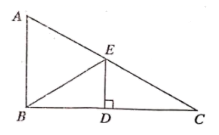
三、解答题
-
15. 解方程:+3=16. 某同学解不等式 出现了错误,解答过程如下:
解:移项,得: (第一步)
合并同类项,得 ≥ ,(第二步)
系数化为1,得 (第三步)
(1)、该同学的解答过程在第步出现了错误,错误原因是.(2)、写出此题正确的解答过程.17. 解不等式组: , 并把解集在数轴上表示出来. 18. 已知在一个十边形中,其中九个内角的和是1302°,求这个十边形另一个内角的度数.19. 如图,在直角△中,∠=90°,是斜边上的高,∠=35°.求:
18. 已知在一个十边形中,其中九个内角的和是1302°,求这个十边形另一个内角的度数.19. 如图,在直角△中,∠=90°,是斜边上的高,∠=35°.求: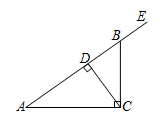 (1)、∠的度数.(2)、∠的度数.20. 长春市以汽车产业为主要经济支柱的工业化城市,新中国的第一辆汽车就是在长春诞生的,某汽车制造厂生产一款电动汽车,计划一个月生产200辆,由于没有足够的熟练工来完成汽车的安装,工人招聘了一批新工人,1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车,求每名熟练工人和新工人每月分别可以安装电动汽车的数量.21. 如图,在 中, 是高线, 是角平分线,它们相交于点 , , .
(1)、∠的度数.(2)、∠的度数.20. 长春市以汽车产业为主要经济支柱的工业化城市,新中国的第一辆汽车就是在长春诞生的,某汽车制造厂生产一款电动汽车,计划一个月生产200辆,由于没有足够的熟练工来完成汽车的安装,工人招聘了一批新工人,1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车,求每名熟练工人和新工人每月分别可以安装电动汽车的数量.21. 如图,在 中, 是高线, 是角平分线,它们相交于点 , , . (1)、求 的度数.(2)、求 的度数.(3)、求 的度数.22. 阅读材料:
(1)、求 的度数.(2)、求 的度数.(3)、求 的度数.22. 阅读材料:课堂上,老师设计了一个活动:将一个4×4的正方形网格沿着网格线划分成两部分(分别用阴影和空白表示),使得这两部分图形是全等的,请同学们尝试给出划分的方法.
约定:如果两位同学的划分结果经过旋转、翻折后能够重合,那么就认为他们的划分方法相同.
小方、小易和小红分别对网格进行了划分,结果如图①、图②、图③所示.
小方说:“我们三个人的划分方法都是正确的.但是将小红的整个图形(图③)逆时针旋转90°后得到的划分方法与我的划分方法(图①)是一样的,应该认为是同一种方法,而小易的划分方法与我的不同.”
老师说:“小方说得对.”

完成下列问题:
(1)、图④的划分方法是否正确?(2)、判断图⑤的划分方法与图②小易的划分方法是否相同,并说明你的理由.(3)、请你再想出一种与已有方法不同的划分方法,使之满足上述条件,并在图⑥中画出来.23. 为庆祝伟大的中国共产党成立100周年,发扬红色传统,传承红色精神,某学校举行了主题为“学史明理,学史增信,学史崇德,学史力行”的党史知识竞赛,一共有25道题,满分100分,每一题答对得4分,答错扣1分,不答得0分.(1)、若某参赛同学只有一道题没有作答,最后他的总得分为86分,则该参赛同学一共答对了多少道题?(2)、若规定参赛者每道题都必须作答且总得分大于或等于90分才可以被评为“学党史小达人”,则参赛者至少需答对多少道题才能被评为“学党史小达人”?24.(1)、【教材呈现】如图是华师版七年级下册数学教材第76页的部分内容.

请根据教材提示,结合图①,将证明过程补充完整.
(2)、【结论应用】如图②,在△中,∠=60°,平分∠ , 平分∠ , 求∠的度数.
(3)、如图③,将△的∠折叠,使点落在△外的点处,折痕为 . 若∠= , ∠= , ∠= , 则、、满足的等量关系为(用、、的代数式表示).