吉林省延边朝鲜族自治州敦化市2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 16的平方根是（）．

A、8 B、4 C、 $\pm 4$ D、 $- 4$

查看试题解析
2. 下列选项中，显示部分在总体中所占百分比的统计图是（）

A、扇形统计图 B、条形统计图 C、折线统计图 D、直方图

查看试题解析
3. 不等式 $x + 1 \geq 2 x - 1$ 的解集在数轴上表示正确的是（）．

A、 B、 C、 D、

查看试题解析
4. 如图所示，直线AB，CD相交于点O，已知∠AOD=160°，则∠BOC的大小为（）

A、20° B、60° C、70° D、160°

查看试题解析
5. 如图，点 $P$ 的坐标可能是（）．

A、 $(2 ， 3)$ B、 $(- 2 ， 3)$ C、 $(- 2 ， - 3)$ D、 $(2 ， - 3)$

查看试题解析
6. 如图，已知 $A B / / C D$ ，点 $E$ 在 $C D$ 上，连接 $A E$ ，作 $E F$ 平分 $∠ A E D$ 交 $A B$ 于点 $F$ ， $∠ A F E = 60 °$ ，则 $∠ A E C$ 的度数为（）．

A、 $∠ A E C = 60 °$ B、 $∠ A E C = 70 °$ C、 $∠ A E C = 80 °$ D、 $∠ A E C = 90 °$

查看试题解析

二、填空题

7. 若x³＝64，则 $\sqrt{x}$ ＝．

查看试题解析
8. 妈妈煮一道菜时，为了了解菜的咸淡是否适合，于是取了一点品尝，这属于（填“全面调查”或“抽样调查”）．

查看试题解析
9. 点 $P (3 + a ， a + 1)$ 到 $x$ 轴距离为3，则点 $P$ 到 $y$ 轴的距离为．

查看试题解析
10. 若关于x、y的二元一次方程3x﹣ay=1有一个解是 ${\begin{array}{l} x = 3 \\ y = 2 \end{array}$ ，则a=.

查看试题解析
11. 如图，想在河堤两岸搭建一座桥，在如图所示的几种搭建方式中，最短的是 $P B$ ，理由是．

查看试题解析
12. 如图，DA⊥CE于点A，CD∥AB，∠1=30°，则∠D= ．

查看试题解析
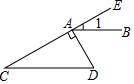13. 若二元一次方程组 ${\begin{array}{l} x + 2 y = 3 \\ 2 x + 2 y = 3 \end{array}$ ，则 $x$ 与 $y$ 的关系是．（写出一个答案即可）．

查看试题解析
14. 某商店以每辆300元的进价购入100辆自行车，并以每辆360元的价格销售，一段时间后自行车的销售款已超过这批自行车的进货款，这时已售出自行车的数量至少为辆．

查看试题解析

三、解答题

15. 计算 $| 1 - \sqrt{4} | + \sqrt{16} + \sqrt[3]{- 27}$ ．

查看试题解析
16. 已知一个正数 $x$ 的平方根是2a-3与5-a，求正数 $x$ ．

查看试题解析
17. 解方程组 ${\begin{array}{l} x - 3 y = 5 & ① \\ 4 x - 3 y = 2 & ② \end{array}$ ．

查看试题解析
18. 解不等式组 ${\begin{array}{l} 2 x - 7 < 3 (x - 1) & ① \\ 5 - \frac{1}{2} (x + 4) \geq x & ② \end{array}$ ．

查看试题解析
19. 如图，已知： $A B / / C D$ ， $∠ B + ∠ D = 180 °$ ．
求证： $B C / / D E$ ．
证明：∵ $A B / / C D$ （已知），
∴∠                  ▲                  ＝∠                  ▲                  （   ）．
∵ $∠ B + ∠ D = 180 °$ （   ），
∴∠                  ▲                   $+ ∠ D = 180 °$ （等量代换）．
∴ $B C / / D E$ （    ）．

查看试题解析
20. 如图，在数轴上，点 $A$ 、 $B$ 分别表示数 $1$ 、 $- 2 x + 3$ .

(1)、求 $x$ 的取值范围.

(2)、数轴上表示数 $- x + 2$ 的点应落在（）

A、点 $A$ 的左边 B、线段 $A B$ 上 C、点 $B$ 的右边

查看试题解析
21. 如图，已知： $A E / / B F$ ， $∠ A = ∠ F$ ，证明： $∠ C = ∠ D$ ．

查看试题解析
22. ${\begin{array}{l} x + y = 2 k \\ x - y = 4 \end{array}$ 的解满足 ${\begin{array}{l} x > 1 \\ y < 1 \end{array}$ ，求 $k$ 的整数值．

查看试题解析
23. 某校团委随机抽取了 $n$ 名本校学生，对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查，问卷中的家庭活动方式包括：
A．在家里聚餐； B．去影院看电影；
C．到公园游玩； D．进行其他活动．
每位学生在问卷调查时都按要求只选择了其中一种喜欢的活动方式，该校团委收回全部调查问卷后，将收集到的数据整理并绘制成如下的统计图．根据统计图提供的信息，解答下列问题：
$n$ 名学生喜欢的家庭活动方式的人数条形统计图

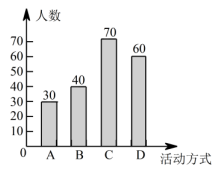(1)、请直接写出n的值；

(2)、四种方式中最受学生喜欢的方式为（用 $A$ ， $B$ ， $C$ ， $D$ 作答）；选择该种方式的学生人数占被调查的学生人数的百分比为；

(3)、根据统计结果，估计该校1200名学生中喜欢 $C$ 方式的学生比喜欢 $B$ 方式的学生多的人数．

查看试题解析
24. 如图，在平面直角坐标系中，已知点 $A (- 3 ， - 1)$ ， $B (- 1 ， - 4)$ ．

(1)、若把线段 $A B$ 向上平移4个单位长度，再向右平移3个单位长度得到线段 $A_{1} B_{1}$ ，画出线段 $A_{1} B_{1}$ ，并直接写出 $A_{1}$ ， $B_{1}$ 的坐标；

(2)、若点 $P (m ， n)$ 在线段 $A B$ 上，则点 $P$ 经过平移后的坐标是；（用含 $m$ ， $n$ 的式子表示）

(3)、连接 $A A_{1}$ 、 $B B_{1}$ ，请直接写出四边形 $A B B_{1} A_{1}$ 的面积．

查看试题解析
25. 为建设“秀美幸福之市”，长沙市绿化提质改造工程正如火如荼地进行，某施工队计划购买甲、乙两种树苗共400棵对芙蓉路的某标段道路进行绿化改造，已知甲种树苗每棵200元，乙种树苗每棵300元．

(1)、若购买两种树苗的总金额为90000元，求需购买甲、乙两种树苗各多少棵？

(2)、若购买甲种树苗的金额不少于购买一中树苗的金额，至少应购买甲种树苗多少棵？

查看试题解析
26. 如图1，在平面直角坐标系中，正方形 $O A B C$ 的面积等于4，长方形 $O A D E$ 的面积等于8，其中点 $C$ 、 $E$ 在 $x$ 轴上，点 $A$ 在 $y$ 轴上．

(1)、请直接写出点 $A$ ，点 $B$ ，点 $D$ 的坐标；

(2)、如图2，将正方形 $O A B C$ 沿 $x$ 轴向右平移，移动后得到正方形 $O^{'} A^{'} B^{'} C^{'}$ ，设移动后的正方形 $O^{'} A^{'} B^{'} C^{'}$ 长方形 $O A D E$ 重叠部分（图中阴影部分）的面积为 $S$ ；
①当 $A A^{'} = 1$ 时， $S =$ ▲ ；当 $A A^{'} = 3$ 时， $S =$ ▲ ；当 $A A^{'} = 5$ 时， $S =$ ▲ ；
②当 $S = 1$ 时，请直接写出 $A A^{'}$ 的值．

查看试题解析