吉林省松原市前郭县2020-2021学年七年级下学期期末考试数学试题

试卷更新日期：2022-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. $(- 0.7)^{2}$ 的平方根是（）

A、−0.7 B、+0.7 C、 $\pm 0.7$ D、0.49

查看试题解析
2. “众志成城，万众一心!”在全国人民共同努力下，新冠肺炎疫情基本可控．为了解校园解封后刚复学时学生的心理健康状况，某中学从该校2000名同学中随机抽取500名同学进行问卷调查，本次调查的样本容量是（）

A、500 B、500名学生的心里健康状况 C、2000 D、2000名学生心里健康状况

查看试题解析
3. 已知点P（2a+4，3a-6）在第四象限，那么a的取值范围是（）

A、-2＜a＜3 B、a＜-2 C、a＞3 D、-2＜a＜2

查看试题解析
4. 已知x=m是关于x的方程2x+m=6的解，则m的值是（）

A、－3 B、3 C、－2 D、2

查看试题解析
5. 象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏.如图，是一局象棋残局，已知表示棋子“馬”和“車”的点的坐标分别为（4，3），（-2，1），则表示棋子“炮”的点的坐标为（）

A、 $(1 ， 3)$ B、 $(3 ， 2)$ C、 $(0 ， 3)$ D、 $(- 3 ， 3)$

查看试题解析
6. 如图，将直角三角形ABC沿AB方向平移得到直角三角形DEF．已知BE＝4，EF＝8，CG＝3，则图中阴影部分的面积为（）

A、16 B、20 C、26 D、12

查看试题解析

二、填空题

7. $\sqrt{6} - \sqrt{3}$ 的相反数是．

查看试题解析
8. 不等式组 ${\begin{array}{l} x > - 5 \\ x < 4 \end{array}$ 的解集是．

查看试题解析
9. 若 $\sqrt{{(x - 3)}^{2}} = 3 - x$ ，则x的取值范围是．

查看试题解析
10. 在体育课上某同学立定跳远的情况如图所示，l表示起跳线，在测量该同学的实际立定跳远成绩时，应测量图中线段PC的长，理由是.

查看试题解析
11. 《九章算术》是我国东汉年间编订的一部数学经典著作，其中有一个问题是：“今有三人公车，二车空；二人公车，九人步．问：人与车各几何？”其大意如下：有若干人要坐车，若每3人坐一辆车，则有2辆空车；若每2人坐一辆车，则有9人需要步行，问人与车各多少？设共有 $x$ 人， $y$ 辆车，则可列方程组为．

查看试题解析
12. 刘伯伯家今年养了4000条鲤鱼，现在准备打捞出售，为估计鱼塘中鲤鱼的总质量，从鱼塘中捕捞了三次进行统计：（见表格）则估计鱼塘中鲤鱼的总质量为 kg．
序号
条数
总质量（kg）
1
25
41
2
10
17
3
15
27

查看试题解析
13. 如图，在平面直角坐标系中， $Δ O A B$ 的顶点A，B的坐标分别为 $(3 ， \sqrt{3})$ ， $(4 ， 0)$ ，把 $Δ O A B$ 沿x轴向右平移得到 $Δ C D E$ ，如果点D的坐标为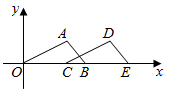 $(6 ， \sqrt{3})$ ，则点E的坐标为.

查看试题解析
14. 如图：AB∥CD，∠2＝2∠1，EG平分∠FED，则∠3＝度．

查看试题解析

三、解答题

15. 计算： $\sqrt[3]{- 27} - \sqrt{(- 4)^{2}} + (\sqrt{5})^{2}$

查看试题解析
16. 下面的不等式解法有不符合题意，按下列要求完成解答：
解不等式： $\frac{2 x + 1}{3} - \frac{x + 2}{6} < 2$ ．
解：去分母得：2（2x+1）﹣x+2＜12      ①
去括号得：4x+2﹣x+2＜12      ②
合并同类项得：3x＜8     ③
解得：x＜ $\frac{8}{3}$         ④

(1)、以上的解法中从哪一步开始出现了错误（写出序号即可）；

(2)、写出正确解答过程并把不等式的解集表示在数轴上．

查看试题解析
17. 解方程组： ${\begin{array}{l} \frac{x}{4} - y = - 1 \\ 3 (x - y) = 2 x \end{array}$ ．

查看试题解析
18. 如图，AD⊥BC于D，EG⊥BC于G，∠E＝∠AHE，那么AD平分∠BAC吗？试说明理由．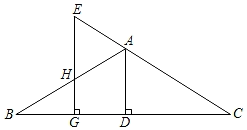

查看试题解析
19. 如图所示的方格纸中每个小正方形都是边长为1个单位长度的小正方形，在平面直角坐标系中，已知A（1，0），B（4，0），C（3，3），D（1，4）．

(1)、描出A、B、C、D四点的位置，并顺次连接ABCD；

(2)、四边形的面积是；

(3)、把四边形向左平移5个单位，再向下平移1个单位得到四边形A₁B₁C₁D₁ ，画出平移后的四边形A₁B₁C₁D₁ ，并写出A₁、C₁的坐标．

查看试题解析
20. 已知 $2 a + 1$ 的平方根是 $\pm 3$ ， $3 a + 2 b - 4$ 的立方根是-2，求 $\sqrt{4 a - 5 b + 8}$ 的立方根．

查看试题解析
21. 如图，∠AGF＝∠ABC，∠1+∠2＝180°．

(1)、试判断BF与DE的位置关系，并说明理由；

(2)、若BF⊥AC，∠2＝150°，求∠AFG的度数．

查看试题解析
22. 已知，关于 $x$ 、 $y$ 的方程组 ${\begin{array}{l} x - y = a + 3 \\ 2 x + y = 5 a \end{array}$ 的解满足 $x < y < 0$ ．

(1)、求 $a$ 的取值范围；

(2)、化简 $| a | - | a + 3 |$ ．

查看试题解析
23. 为了解某市2021年初中毕业生的实验考查成绩等级的分布情况，随机抽取了该市若干名学生的实验考查成绩进行统计分析，并根据抽取的成绩绘制了如下统计表和统计图：
成绩等级
A
B
C
D
人数
60
x
30
10
百分比
30%
50%
15%
y
请根据以上统计表和统计图提供的信息，解答下列问题：

(1)、表中x、y所表示的数分别为：x＝， y＝；

(2)、本次抽查的学生有名；

(3)、请补全条形统计图；

(4)、根据抽样调查结果，请你估计2021年该县60000名初中毕业生实验考察成绩为D等级的学生人数．

查看试题解析
24. 综合与实践
问题背景

如图，在平面直角坐标系中，点A的坐标为（﹣3，5），点B的坐标为（0，1），点C的坐标为（4，5），将线段AB沿AC方向平移，平移距离为线段AC的长度．

(1)、动手操作
画出AB平移后的线段CD，直接写出B的对应点D的坐标；

(2)、探究证明
连接BD，试探究∠BAC，∠BDC的数量关系，并证明你的结论；

(3)、拓展延伸
若点E在线段BD上，连接AD，AE，且满足∠EAD＝∠CAD，请求出∠ADB：∠AEB的值，并写出推理过程．

查看试题解析
25. 某商店需要购进甲、乙两种商品共160件，其进价和售价如表：

甲
乙
进价（元/件）
15
35
售价（元/件）
20
45

(1)、若商店计划销售完这批商品后能获利1100元．则甲、乙两种商品应分别购进多少件？

(2)、若商店计划投入资金不多于4300元，且销售完这批商品获利多于1260元，商店有哪几种购货方案？哪种购货方案销售利润最大？请说明理由．

查看试题解析
26. 如图，四边形OABC为长方形，以O为坐标原点，OC所在直线为x轴建立平面直角坐标系．已知点A的坐标为（0，5），点C的坐标为（9，0）．

(1)、直接写出点B的坐标为；

(2)、有一动点D从原点O出发，以1个单位长度/秒的速度沿线段OA向终点A运动，当直线CD将长方形的周长分为3：4两部分时，求D点的运动时间t值；

(3)、在（2）的条件下，点E为坐标轴上一点，若三角形CDE的面积为18，直接写出点E的坐标．

查看试题解析

序号	条数	总质量（kg）
1	25	41
2	10	17
3	15	27

成绩等级	A	B	C	D
人数	60	x	30	10
百分比	30%	50%	15%	y

	甲	乙
进价（元/件）	15	35
售价（元/件）	20	45