吉林省吉林市永吉县2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 若x²＝4，则x的值（）

A、2 B、±2 C、16 D、±16

查看试题解析
2. 下列各数是无理数的是（）

A、 $\frac{1}{3}$ B、 $\sqrt{4}$ C、 $- \frac{3}{4}$ D、 $\sqrt{8}$

查看试题解析
3. 不等式组 ${\begin{array}{l} - 3 x \leq 6 \\ - (x - 3) > 2 (2 - x) \end{array}$ 的解集在数轴上表示正确的是（）

A、 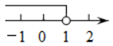B、 C、 D、

查看试题解析
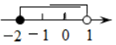4. 在平面直角坐标系中，将点A（﹣2，﹣3）先向左平移1个单位长度，再向上平移3个单位长度，所得到的点的坐标为（）

A、（﹣3，0） B、（﹣1，6） C、（﹣3，﹣6） D、（﹣1，0）

查看试题解析
5. 实数a＞b，则下列变形中不正确的是（）

A、a﹣2＞b﹣2 B、5a＞5b C、﹣2a＞﹣2b D、 $\frac{a}{3} > \frac{b}{3}$

查看试题解析
6. 下列调查：①了解全班同学每周体育锻炼的时间；②调查市场上某种食品的色素含量是否符合国家标准；③鞋厂检测生产的鞋底能承受的弯折次数；④了解全班同学的数学学科期末考试成绩．其中适合用抽样调查的是（）

A、①② B、②③ C、③④ D、①④

查看试题解析

二、填空题

7. 计算： $\sqrt{{(- 2)}^{2}}$ ＝．

查看试题解析
8. 如图，直线a，b被直线c所截，并且 $a / / b$ ，若∠1＝108°，则∠2的度数是．

查看试题解析
9. 若x＝2，y＝﹣1是关于x，y的二元一次方程2mx+4ny﹣9＝3的一个解，则m﹣n的值为．

查看试题解析
10. 在平面直角坐标系中，若点A（m，n）满足 $\sqrt{m + 2021}$ +|n﹣2020|＝0，则点A在第象限．

查看试题解析
11. 不等式 $\frac{2 x - 3}{3}$ ≤1的正整数解有个．

查看试题解析
12. 如图，某人从点A沿北偏东60°的方向行走到点B，再从点B沿南偏西20°方向行走到点C，则∠ABC的度数为．

查看试题解析
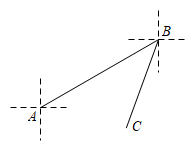13. 如图，将 $△$ ABC沿BC方向平移2 $c m$ ，得到 $△$ DEF．若四边形ABFD的周长为18 $c m$ ，则 $△$ ABC周长为 $c m$ ．

查看试题解析
14. 丁丁参加了一次智力竞赛，共回答了30道题，题目的评分标准是这样的：答对一题加5分，答错或不答一题倒扣1分．如果在这次竞赛中丁丁的得分要超过100分，那么他至少要答对题．

查看试题解析

三、解答题

15. 计算：（ $\sqrt{4} - \sqrt{3}$ ）+|﹣ $\sqrt{3}$ |﹣ $\sqrt[3]{- 27}$ ．

查看试题解析
16. 解方程组： ${\begin{array}{l} 9 x + 4 y = 14 \\ 3 x - 2 y = 8 \end{array}$ ．

查看试题解析
17. 解不等式： $\frac{5 x + 1}{6} - 2 > \frac{x - 5}{4}$ ，并把解集在数轴上表示出来．

查看试题解析
18. 解不等式组 ${\begin{array}{l} 2 x - 1 > x + 1 \\ x + 8 < 4 x - 1 \end{array}$ .

查看试题解析
19. 如图，在 $△$ ABC中，过AB上任意一点D作 $D E / / A C$ 交BC于点E，以E为顶点，ED为一边，作∠DEF＝∠A，另一边EF交AC于F．

(1)、EF与AB平行吗？说明理由；

(2)、若∠ABC＝30°，∠ACB＝40°，则∠EFC的度数为．

查看试题解析
20. 在平面直角坐标系中，已知：点P（2m+4，m﹣1）．

(1)、分别根据下列条件，求出点P的坐标：
①点P在y轴上；
②点P的纵坐标比横坐标大3；

(2)、点P 是坐标原点（填“可能”或“不可能”）．

查看试题解析
21. 在平面直角坐标系中，A，B，C，C₁四点的坐标分别为A（﹣6，7），B（﹣3，0），C（0，3），C₁（5，1）．

(1)、在平面内画出 $△$ ABC， $△$ ABC的面积为；

(2)、将 $△$ ABC平移得到 $△$ A₁B₁C₁ ，使点C与点C₁重合．
①画出 $△$ A₁B₁C₁（点A的对应点是A₁ ，点B的对应点是B₁）；
②已知点P（﹣3，m）为 $△$ ABC内一点，点P随着 $△$ ABC平移到点Q（n，1），则m＝ ▲ ， n＝ ▲ ．

查看试题解析
22. 某市教育行政部门为了了解七年级学生每学期参加公益活动的情况，抽样调查了某中学学生一个学期参加公益活动的天数，并用得到的数据绘制了如图所示两幅不完整的统计图．

(1)、扇形统计图中a的值是，该校七年级学生共有人；

(2)、在该次抽样调查中，参加活动时间为5天的学生共有（）人，并补全条形统计图；

(3)、如果该市七年级学生共有20000人，估计这20000人中，参加公益活动时间不少于4天的学生有多少人？

查看试题解析
23. 如图，已知DC∥FP，∠1＝∠2，∠AGF＝80°，∠DEF＝30°，FH平分∠EFG．

(1)、说明：DC∥AB；

(2)、求∠PFH的度数．

查看试题解析
24. 问题解决

(1)、糖葫芦一般是用竹签串上山楂，再蘸以冰糖制作而成．现将一些山楂分别串在若干根竹签上．如果每根竹签串5个山楂，还剩余4个山楂；如果每根竹签串8个山楂，还剩余7根竹签．这些竹签有多少根？山楂有多少个？

(2)、现有 $a$ 根竹签， $b$ 个山楂．若每根竹签串 $c$ 个山楂，还剩余 $d$ 个山楂，则下列等式成立的是（填写序号）．
⑴ $b c + d = a$ ；⑵ $a c + d = b$ ；⑶ $a c - d = b$ ．

查看试题解析
25. 如图，在平面直角坐标系中，已知：OA＝2，OB＝3．现同时将点A和点B向上平移2个单位长度，再向右平移2个单位长度，分别得到点A和点B的对应点C和D，连接AC，BD，CD．

(1)、直接写出点A，B，C，D的坐标；

(2)、CD＝，S_四_边_形ABDC＝；

(3)、在线段OC上是否存在一点P，使 $S_{△ C D P} ＝ S_{△ O B P}$ ，如果存在，求出点P的坐标；若不存在，说明理由．

查看试题解析
26. 某快递公司准备购买机器人来代替人工分拣．已知购买1台甲型机器人比购买1台乙型机器人多2万元；购买2台甲型机器人和3台乙型机器人共需24万元．

(1)、求甲、乙两种型号的机器人每台的价格分别为多少万元？

(2)、已知甲、乙两种型号的机器人每台每小时分拣快递分别为1200件和1000件，该公司计划最多用39万元购买8台这两种型号的机器人，通过计算说明该公司如何购买，才能使得每小时的分拣量最大？

查看试题解析