吉林省吉林市桦甸市2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点 $P (2 ， - 1)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列各数属于无理数的是（）

A、 $\frac{22}{7}$ B、3.14159 C、 $\sqrt[3]{2}$ D、 $\sqrt{36}$

查看试题解析
3. 已知实数a、b，若a＞b，则下列结论正确的是

A、 $a - 5<b - 5$ B、 $2 + a<2 + b$ C、 $(- 4 ， - 6)$ D、 $3a>3b$

查看试题解析
4. 下列调查中，适合用全面调查方式的是（）

A、了解某校七年级学生期末数学考试的成绩 B、了解一批签字笔的使用寿命 C、了解市场上酸奶的质量情况 D、了解春节联欢晚会的收视率

查看试题解析
5. 如图，下列条件中能判定AB $//$ CD的是（）

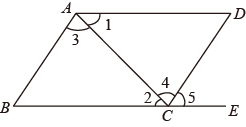A、∠1=∠2 B、∠3=∠4 C、∠B=∠D D、∠D=∠5

查看试题解析
6. 足球比赛的记分办法为：胜一场得3分，平一场得1分，负一场得0分.一个队打了14场比赛，负5场，共得19分，那么这个队胜了（）

A、3场 B、4场 C、5场 D、6场

查看试题解析

二、填空题

7. 若剧院里11排5号可以用 $(11 ， 5)$ 表示，则 $(7 ， 8)$ 表示．

查看试题解析
8. 若第四象限内的点 $P (x ， y)$ 满足 $| x | = 4$ ， $y^{2} = 9$ ，则点P的坐标是．

查看试题解析
9. 若 $x^{3 m - 8} - 2 y^{n - 1} = 5$ 是二元一次方程，则 $m^{n} =$ ．

查看试题解析
10. 如图，点A，C，F，B在同一直线上，CD平分 $∠ ECB$ ， $FG ∥ CD$ ，若 $∠ E C D$ 的度数为70°，则 $∠ G F B$ 的度数为．

查看试题解析
11. 如果关于x的一元一次不等式组的解集在数轴上的表示如图所示，那么该不等式组的解集为．

查看试题解析
12. 若 $\sqrt{x + 1}$ ＝1，则﹣（2x﹣3）＝．

查看试题解析
13. 如图，若 $∠ 1 = ∠ D = 40 °$ ， $∠ C + ∠ D = 90 °$ ，则 $∠ B =$ ．

查看试题解析
14. 为了解某市2019年中考数学学科各分数段成绩分布情况，从中抽取400名考生的中考数学成绩进行统计分析，在这个问题中，样本容量是．

查看试题解析

三、解答题

15. 计算： $\sqrt{4} + | - 3 | + \sqrt[3]{27} + {(- 1)}^{2021}$ ．

查看试题解析
16. 解二元一次方程组： ${\begin{array}{l} 3 x - 5 y = 6 \\ x + 4 y = - 15 \end{array}$ ．

查看试题解析
17. 已知：如图， $∠ 1 + ∠ 2 = 180 °$ ，求证： $a ∥ b$ .

查看试题解析
18. 小张把两个大小不同的苹果放到天平上称，当天平保持平衡时的砝码重量如图所示．问：这两个苹果的重量分别为多少g？

查看试题解析
19. 如图所示，已知 $B E ∥ F G$ ， $∠ 1 = ∠ 2$ ．求证 $D E ∥ B C$ ．

查看试题解析
20. 解不等式组 ${\begin{array}{l} 3 x < x + 8 \\ 4 (x + 1) \leq 7 x + 10 \end{array}$ ，并把解集表示在数轴上．

查看试题解析
21. 如图所示，在平面直角坐标系中，点 $A (- 1 ， 5)$ ， $B (- 1 ， 0)$ ， $C (- 4 ， 3)$ ．

(1)、求 $△ A B C$ 的面积；

(2)、画出 $△ A B C$ 向右平移5个单位长度后得到的 $△ A_{1} B_{1} C_{1}$ ；

(3)、写出（2）中平移后的三角形 $A_{1} B_{1} C_{1}$ 顶点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标．

查看试题解析
22. 已知 $2 m + 2$ 的平方根是 $\pm 4$ ， $3 m + n + 4$ 的立方根是3．求 $m + n$ 的平方根．

查看试题解析
23.
如图，已知∠1=∠2，∠C=∠D，求证：∠A=∠F．

查看试题解析
24. “世界读书日”前夕，某校开展了“读书助我成长”的阅读活动．为了了解该校学生在此次活动中课外阅读书籍的数量情况，随机抽取了部分学生进行调查，将收集到的数据进行整理，绘制出两幅不完整的统计图，请根据统计图信息解决下列问题：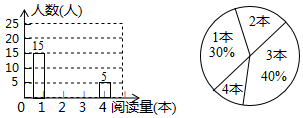

(1)、求本次调查中共抽取的学生人数；

(2)、补全条形统计图；

(3)、在扇形统计图中，阅读 $2$ 本书籍的人数所在扇形的圆心角度数是；

(4)、若该校有 $1200$ 名学生，估计该校在这次活动中阅读书籍的数量不低于 $3$ 本的学生有多少人？

查看试题解析
25. 某商场的运动服装专柜，对 $A ， B$ 两种品牌的运动服分两次采购试销后，效益可观，计划继续采购进行销售．已知这两种服装过去两次的进货情况如下表．

第一次
第二次
$A$ 品牌运动服装数/件
20
30
$B$ 品牌运动服装数/件
30
40
累计采购款/元
10200
14400

(1)、问 $A ， B$ 两种品牌运动服的进货单价各是多少元？

(2)、由于 $B$ 品牌运动服的销量明显好于 $A$ 品牌，商家决定采购 $B$ 品牌的件数比 $A$ 品牌件数的 $\frac{3}{2}$ 倍多5件，在采购总价不超过21300元的情况下，最多能购进多少件 $B$ 品牌运动服？

查看试题解析
26. 如图，在平面直角坐标系中，点A，B的坐标分别为 $(- 1 ， 0)$ ， $(3 ， 0)$ ，现同时将点A，B分别向上平移2个单位长度，再向右平移1个单位长度，得到A，B的对应点C，D，连接AC，BD，CD．

(1)、直接写出点C，点D的坐标为C ， D；

(2)、求出四边形ABDC的面积；

(3)、在x轴上是否存在一点F，使得 $△ D F C$ 的面积是 $△ D F B$ 面积的4倍，若存在，请求出点F的坐标，若不存在，请说明理由．

查看试题解析

	第一次	第二次
$A$ 品牌运动服装数/件	20	30
$B$ 品牌运动服装数/件	30	40
累计采购款/元	10200	14400