吉林省白山市靖宇县2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-04-28 类型：期末考试

进入出卷网下载

一、单选题

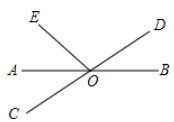
1. 下面调查中，最适合采用全面调查的是（）

A、对全国中学生视力状况的调查 B、了解吉林省七年级学生身高情况 C、调查人们保护海洋的意识 D、对“玉兔二号”月球车零部件的调查

查看试题解析
2. 下列实数： $\frac{22}{7}$ ， 3.14159265， $\sqrt{7}$ ， -8， $\sqrt[3]{2}$ ， 0.6，0， $\sqrt{36}$ ， $\frac{π}{3}$ 无理数的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 已知x＜y，则下列结论成立的是（）

A、x﹣2＞y﹣2 B、﹣2x＞﹣2y C、3x+1＞3y+1 D、 $\frac{x}{2} ＞ \frac{y}{2}$

查看试题解析
4. 为了解七年级1000名学生的身高情况，从中抽取了300名学生的身高进行统计．这300名学生的身高是（）

A、总体的一个样本 B、个体 C、总体 D、样本容量

查看试题解析
5. 如图，三条直线相交于点 $O$ ．若 $C O ⊥ A B$ ， $∠ 1 = 52 °$ ，则 $∠ 2$ 等于（）

A、 $52 °$ B、 $28 °$ C、 $38 °$ D、 $48 °$

查看试题解析
6. 如图所示，在灌溉农田时，要把河（直线 $l$ 表示一条河）中的水引到农田 $P$ 处，设计了四条路线 $P A 、 P B 、 P C 、 P D$ ，你选择哪条路线挖渠才能使渠道最短（）

A、 $P A$ B、 $P B$ C、 $P C$ D、 $P D$

查看试题解析

二、填空题

7. “ $a$ 与5的和是非正数”用不等式表示为．

查看试题解析
8. 在数据25，23，21，29，28，25，22，26，28，26，26，27，25，21，29中，范围在 $25 \sim 27$ （包括前边的数，不包括后边的数）这一组的频数是．

查看试题解析
9. 命题“同位角相等”是（填“真”或“假”，）命题

查看试题解析
10. 算术平方根是 $\sqrt{5}$ 的实数是．

查看试题解析
11. 计算： $\sqrt{3} － | － \sqrt{3} | + \sqrt{9} + \sqrt[3]{- 8} =$ ．

查看试题解析
12. 在平面直角坐标系中，若点 $M (a ， 4)$ 在第二象限，则点 $P (1 - a ， a)$ 在第象限．

查看试题解析
13. 如图，小强同学统计了他家5月份的长途电话明细清单，按通话时间画出直方图，观察直方图，通话时间不超过5 $m i n$ 的次数是次．

查看试题解析
14. 如图， $△ O A B$ 的顶点 $B$ 的坐标是（5，0），把 $△ O A B$ 沿 $x$ 轴向右平移得到 $△ C D E$ ，如果 $C$ 点坐标是（3，0），那么 $O E$ 的长为．

查看试题解析

三、解答题

15. 解不等式 $\frac{x + 3}{5} < \frac{2 x - 5}{3}$ ，并把解集在数轴上表示出来．

查看试题解析
16. 如图，已知直线 $A B$ 、 $C D$ 相交于点 $O$ ， $O A$ 平分 $∠ E O C$ ， $∠ E O C = 7 0^{∘}$ ，求 $∠ B O D$ 的度数．

查看试题解析
17. 如图所示，完成下列推理
已知 $A B / / C D$ ， $M N$ 分别交 $A B 、 C D$ 于点 $E 、 F$ ， $∠ 1 = ∠ 2$ ．
求证： $E P / / F Q$ ．
证明：∵ $A B / / C D$ （已知）
∴ $∠ M E B = ∠ M F D$ （  ）
又∵ $∠ 1 = ∠ 2$ （  ）
∴ $∠ M E B - ∠ 1 = ∠ M F D - ∠ 2$ （  ）
即 $∠ M E P = ∠$                   ▲
∴ $E P / / F Q$ （  ）

查看试题解析
18. $x$ 取哪些整数时，不等式 $7 x + 2 > 5 (x - 1)$ 与 $\frac{3}{2} x - 1$ ≤ $7 - \frac{5}{2} x$ 都成立？

查看试题解析
19.

(1)、解方程组： ${\begin{array}{l} 4 (x - y - 1) = 3 (1 - y) - 2 \\ \frac{x}{2} + \frac{y}{3} = 2 \end{array}$ ；

(2)、在等式 $y = k x + b$ 中，当 $x = - 1$ 时 $y = 0$ ；当 $x = 2$ 时， $y = 3$ ．试求当 $x = - 3$ 时， $y$ 的值?

查看试题解析
20. 已知 $2 a + 3$ 的立方根是3， $a + b - 1$ 的算术平方根是4， $c$ 是 $\sqrt{11}$ 的整数部分．

(1)、求 $a$ ， $b$ ， $c$ 的值．

(2)、求 $a - 4 b + 3 c$ 的平方根．

查看试题解析
21. 在“全国安全教育日”来临之际，我县某学校举行了安全知识竞赛，学校随机抽取了部分参赛学生的成绩进行整理．根据成绩绘制成不完整的频数分布表和频数分布直方（每组包含最小值，不包含最大值）：
成绩
频数
百分比
60---70
15
$m$
70---80
20
40％
80---90
$n$
20％
90---100
5
10％
请根据上述统计图表信息，解答下列问题：

(1)、共抽取了名学生进行调查，m= ， n= ．

(2)、补全频数分布直方图．

(3)、若全校有2000名学生，成绩80分及以上者为“优秀”，根据抽样调查结果，估计该校学生得“优秀”等次的学生有人？

查看试题解析
22. 小明准备用80元钱买甲、乙两种饮料共12瓶．已知甲种饮料每瓶8元，乙种饮料每瓶5元，小明最多能买甲种饮料多少瓶？

查看试题解析
23. 已知 $△ A B C$ 经过平移后得到 $△ A^{'} B^{'} C^{'}$ ，它们各顶点在平面直角坐标系中的坐标如下表所示：
$△ A B C$
$A$ （ $a$ ， 1）
$B$ （3，0）
$C$ （4，4）
$△ A^{'} B^{'} C^{'}$
$A^{'}$ （4，2）
$B^{'}$ （7， $b$ ）
$C^{'}$ （8，5）

(1)、观察表中各对应点坐标的变化，并填空： $a =$ ， $b =$ ．

(2)、在平面直角坐标系中画出 $△ A B C$ 及平移后的 $△ A^{'} B^{'} C^{'}$ ．

(3)、 $△ A^{'} B^{'} C^{'}$ 的面积是．

查看试题解析
24. 列二元一次方程组解答下列问题：
在新冠肺炎疫情防控期间，有快、慢两辆汽车分别从相距180千米的甲、乙两地同时出发匀速行驶，运送医疗物资．如果两车相向行驶，那么1.2小时后两车相遇，如果两车同向行驶，那么6小时后，快车追上慢车，求快车和慢车的速度各是多少？

查看试题解析
25. 【阅读探究】如图1，已知 $A B / / C D$ ， $E 、 F$ 分别是 $A B 、 C D$ 上的点，点 $M$ 在 $A B 、 C D$ 两平行线之间， $∠ A E M = 45 °$ ， $∠ C F M = 25 °$ ，求 $∠ E M F$ 的度数．
解：过点 $M$ 作 $M N / / A B$
∵ $A B / / C D$
∴ $M N / / C D$
∴ $∠ E M N = ∠ A E M = 45 °$
$∠ F M N = ∠ C F M = 25 °$
∴ $∠ E M F = ∠ E M N + ∠ F M N$
$= 45 ° + 25 °$
$= 70 °$

(1)、从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将 $∠ A E M$ 和 $∠ C F M$ “凑”在一起，得出角之间的关系，使问题得以解决．进一步研究，我们可以发现图1中 $∠ A E M 、$ $∠ E M F$ 和 $∠ C F M$ 之间存在一定的数量关系，请直接写出它们之间的数量关系：．

(2)、【方法运用】如图2，已知 $A B / / C D$ ，点 $E 、 F$ 分别在直线 $A B 、 C D$ 上，点 $M$ 在 $A B 、 C D$ 两平线之间，求 $∠ A E M 、 ∠ E M F$ 和 $∠ C F M$ 之间的数量关系．

(3)、【应用拓展】如图3，在图2的条件下，作 $∠ A E M$ 和 $∠ C F M$ 的平分线 $E P$ 、 $F P$ ，交于点 $P$ （交点 $P$ 在两平行线 $A B 、 C D$ 之间）若 $∠ E M F$ $= 60 °$ ，求 $∠ E P F$ 的度数．

查看试题解析
26. 某出租车公司有 $A 、 B$ 两种不同型号的汽车，用两辆 $A$ 型车和一辆 $B$ 型车装满货物一次可运货10吨；用一辆 $A$ 型车和两辆 $B$ 型车装满货物一次可运货11吨．某物流公司现有31吨货物，计划同时租用 $A$ 型车 $a$ 辆和 $B$ 型车 $b$ 辆，一次运完，且恰好每辆车都装满货物．
根据以上信息，解答下列问题：

(1)、一辆 $A$ 型车和一辆 $B$ 型车都装满货物一次可分别运货多少吨？

(2)、请你帮该物流公司设计租车方案．

(3)、若 $A$ 型车每辆需租金200元/次， $B$ 型车每辆需租金240元/次．该物流公司最省钱的租车方案是，最少租车费为元．

查看试题解析

成绩	频数	百分比
60---70	15	$m$
70---80	20	40％
80---90	$n$	20％
90---100	5	10％

$△ A B C$	$A$ （ $a$ ， 1）	$B$ （3，0）	$C$ （4，4）
$△ A^{'} B^{'} C^{'}$	$A^{'}$ （4，2）	$B^{'}$ （7， $b$ ）	$C^{'}$ （8，5）