黑龙江省齐齐哈尔市富拉尔基区2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列几个数中，属于无理数的是（）

A、 $\frac{1}{3}$ B、 $\sqrt{4}$ C、 $\frac{π}{2}$ D、 $3 . \overset{\cdot}{1}$

查看试题解析
2. 下列各式计算正确的是（）

A、 $\sqrt{16} = \pm 4$ B、 $- \sqrt[3]{- 8} = 2$ C、 $\sqrt{{(- 2)}^{2}} = - 2$ D、 $- \sqrt{0.1} = - 0.1$

查看试题解析
3. 适用于全面调查的是（）

A、调查一批灯泡的使用寿命 B、调查全国中学生用于体育锻炼的时间 C、进行第八次全国人口普查 D、调查全市居民收入情况

查看试题解析
4. 如图，已知AB∥CD，∠1＝135°，则∠A的度数为（）

A、40° B、45° C、135° D、145°

查看试题解析
5. 下列说法正确的是（）

A、两直线平行，同旁内角相等 B、直线外一点到这条直线的垂线的长度叫做点到直线的距离 C、过一点有且只有一条直线与已知直线垂直 D、图形平移后，对应点所连线段平行（或在同一直线上）且相等

查看试题解析
6. 点P的坐标为（3，5），点G到P的距离为4个单位长度，且PG∥x轴，则点G的坐标为（）

A、（7，5） B、（1，5） C、（7，5）或（﹣1，5） D、（3，9）或（3，1）

查看试题解析
7. 《孙子算经》中有一道题：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，本木长几何？”译文是：“用一根绳子量一根木头，绳子剩余4.5尺；将绳子对折再量木条，木条剩余1尺，问木条多少尺？”如果设木条长x尺，绳子长y尺，可列方程组（）

A、 ${\begin{array}{l} y + 4.5 = x \\ 2 y + 1 = x \end{array}$ B、 ${\begin{array}{l} y - 4.5 = x \\ \frac{1}{2} y + 1 = x \end{array}$ C、 ${\begin{array}{l} y + 4.5 = x \\ \frac{1}{2} y + 1 = x \end{array}$ D、 ${\begin{array}{l} y - 4.5 = x \\ 2 y + 1 = x \end{array}$

查看试题解析
8. 校园举行足球比赛，胜一场得3分，平一场得1分，输一场得0分；七年一班共进行了12场比赛，获得19分，则七年一班获胜的场数有几种情况（）

A、1种 B、2种 C、3种 D、4种

查看试题解析
9. 在平面直角坐标系中，点A（2x﹣5，6﹣2x）在第四象限，则x的取值范围是（）

A、x＞3 B、x＜3 C、x＜ $\frac{5}{2}$ D、x＞ $\frac{5}{2}$

查看试题解析
10. 已知a、b、c三点在数轴上的位置，如图所示，则下列式子：①a+b＞c+b；②﹣ac＜﹣bc；③ab＜bc；④﹣b+a＜﹣b+c．其中正确的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

11. $\sqrt{16}$ 的平方根是．

查看试题解析
12. 如图所示，添加一个条件使得AB∥CD．

查看试题解析
13. 已知|y﹣3|与（x²﹣4）²互为相反数，则xy的值为．

查看试题解析
14. 把命题“对顶角相等”改写成“如果⋯那么⋯”的形式，正确的改写应为．

查看试题解析
15. 已知∠A＝55°，∠B的两边与∠A的两边分别平行，则∠B的度数为．

查看试题解析
16. 关于x的不等式组 ${\begin{array}{l} 2 x + 4 > 3 x + 1 \\ x - 1 > \frac{x + a}{2} \end{array}$ 有且只有4个整数解，则a的取值范围是．

查看试题解析
17. 在平面直角坐标系中，点A与原点重合，将点A向右平移1个单位长度得到点A₁ ，将A₁向上平移2个单位长度得到点A₂ ，将A₂向左平移3个单位长度得到A₃ ，将A₃向下平移4个单位长度得到A₄ ，将A₄向右平移5个单位长度得到A₅…按此方法进行下去，则A₂₀₂₁点坐标为．

查看试题解析

三、解答题

18.

(1)、计算： $- 1^{3} + | 1 - \sqrt{2} | + \sqrt[3]{8} + \sqrt{0.04}$ ．

(2)、解方程组： ${\begin{array}{l} 3 (y - x - 2) = 1 - 2 (x + 2) \\ \frac{x + 1}{3} - 1 = \frac{y - 2}{2} \end{array}$ ．

查看试题解析
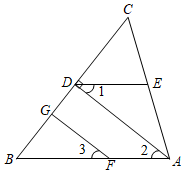
19. 解不等式组： ${\begin{array}{l} 2 x + 3 (x - 2) ＜ 4 ， ① \\ \frac{x + 3}{2} ＜ \frac{2 x - 5}{3} + 3 ； ② \end{array}$ 并把解集在数轴上表示出来.

查看试题解析
20. 完成下面的证明：如图：已知AD⊥BC于点D，DE∥AB，∠1＝∠3，求证：FG⊥BC．
证明：∵DE∥AB（已知），
∴∠1＝∠2（  ），
又∵∠1＝∠3（已知），
∴∠2＝∠3（  ），
∴  ▲  （  ），
∴∠BGF＝  ▲  （               ），
∴AD⊥BC（已知），
∴∠BDA＝90°（  ），
∴  ▲  （等量代换），
∴FG⊥BC（垂直定义）．

查看试题解析
21. 在平面直角坐标系中，△ABC的三个顶点如图所示，点A₁的坐标是（﹣2，1），将△ABC平移使得点A与点A₁重合，点B与点C的对应点分别为B₁、C₁ ．

(1)、请在平面直角坐标系中，画出平移后的△A₁B₁C₁；

(2)、直接写出B₁、C₁坐标；

(3)、计算△A₁BC₁的面积．

查看试题解析
22. 某校为了检测学生身体素质，在全校1500名学生中抽出一部分同学进行1分钟跳绳测试，测试结果如下：
1分钟跳绳次数n
110≤n＜120
n≥120
n≥130
n≥140
150≤n≤160
人数（名）
8
42
36
25
9
根据图中信息，回答下列问题：

(1)、本次共调查了名学生；

(2)、补全直方图（并标注频数）；

(3)、学生1分钟跳绳不低于140次为优秀，根据以上数据，全校学生中大约有多少人跳绳为优秀．

查看试题解析
23. 如图1，CE平分∠ACD，AE平分∠BAC，且∠EAC+∠ACE＝90°．

(1)、请判断AB与CD的位置关系，并说明理由；

(2)、如图2，当∠E＝90°且AB与CD的位置关系保持不变，当直角顶点E点移动时，写出∠BAE与∠ECD的数量关系，并说明理由；

(3)、如图3，P为线段AC上一定点，点Q为直线CD上一动点，且AB与CD的位置关系保持不变，当点Q在射线CD上运动时（点C除外），∠CPQ+∠CQP与∠BAC有何数量关系？写出结论，并加以证明．

查看试题解析
24. 为了防控疫情，学校积极进行校园环境消毒，购买了甲和乙两种浓度的消毒液共100瓶，一共用了680元钱，甲消毒液6元/瓶，乙消毒液8元/瓶．

(1)、求甲、乙两种消毒液各购买多少瓶；

(2)、因环境消毒要求提高，学校准备再次购买这两种消毒液，购买的甲消毒液数量是乙消毒液的数量的一半（不算第一次购买），且再次购买所需费用不超过880元，求甲消毒液最多再次购买多少瓶？

查看试题解析

1分钟跳绳次数n	110≤n＜120	n≥120	n≥130	n≥140	150≤n≤160
人数（名）	8	42	36	25	9