黑龙江省牡丹江市林口县2020-2021学年七年级下学期期末考试数学试题
试卷更新日期:2022-04-28 类型:期末考试
一、单选题
-
1. 如图所示,由下图平移得到的图案是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 在实数 , , , , ,0中,无理数的个数为( )A、1个 B、2个 C、3个 D、4个3. 不等式6﹣3x>0的解集在数轴上表示为( )A、
2. 在实数 , , , , ,0中,无理数的个数为( )A、1个 B、2个 C、3个 D、4个3. 不等式6﹣3x>0的解集在数轴上表示为( )A、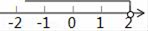 B、
B、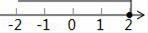 C、
C、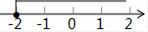 D、
D、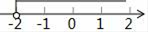 4. 如图,10块形状、大小相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为x厘米和y厘米,则依题意可列方程组为( )
4. 如图,10块形状、大小相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为x厘米和y厘米,则依题意可列方程组为( ) A、 B、 C、 D、5. 如图,已知 , , 平分 , 则( )
A、 B、 C、 D、5. 如图,已知 , , 平分 , 则( ) A、32° B、60° C、58° D、64°6. 若是关于x、y的二元一次方程ax-5y=1的解,则a的值为( )A、-5 B、-1 C、9 D、117. 下列四个命题是真命题的是( )A、两条直线被第三条直线所截,同位角相等 B、互补的两个角一定是邻补角 C、在同一平面内,垂直于同一条直线的两条直线互相平行 D、相等的角是对顶角8. 在一个样本中,40个数据分别落在5个小组内,第1,2,3,5小组的频数分别是6,5,15,7,则第4小组的频数是( )A、7 B、8 C、9 D、109. 下列四个命题:①若a>b,则a-3>b-3;②若a>b,则a+c>b+c;③若a>b,则-3a<-3b;④若a>b,则ac>bc.其中,真命题有( )A、①③④ B、②③④ C、①②③④ D、①②③10. 如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC︰∠EOD=2︰3,则∠BOD的度数为( )
A、32° B、60° C、58° D、64°6. 若是关于x、y的二元一次方程ax-5y=1的解,则a的值为( )A、-5 B、-1 C、9 D、117. 下列四个命题是真命题的是( )A、两条直线被第三条直线所截,同位角相等 B、互补的两个角一定是邻补角 C、在同一平面内,垂直于同一条直线的两条直线互相平行 D、相等的角是对顶角8. 在一个样本中,40个数据分别落在5个小组内,第1,2,3,5小组的频数分别是6,5,15,7,则第4小组的频数是( )A、7 B、8 C、9 D、109. 下列四个命题:①若a>b,则a-3>b-3;②若a>b,则a+c>b+c;③若a>b,则-3a<-3b;④若a>b,则ac>bc.其中,真命题有( )A、①③④ B、②③④ C、①②③④ D、①②③10. 如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC︰∠EOD=2︰3,则∠BOD的度数为( )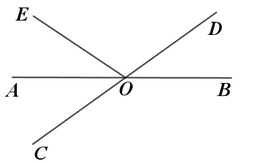 A、36° B、40° C、35° D、45°11. 若方程组的解满足x+y>0,则m的取值范围是( )A、m>﹣3 B、m>﹣2 C、m>﹣1 D、m>012. 如图,现给出下列条件:① , ② , ③ , ④ , ⑤ . 其中能够得到ABCD的条件的个数( )
A、36° B、40° C、35° D、45°11. 若方程组的解满足x+y>0,则m的取值范围是( )A、m>﹣3 B、m>﹣2 C、m>﹣1 D、m>012. 如图,现给出下列条件:① , ② , ③ , ④ , ⑤ . 其中能够得到ABCD的条件的个数( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
13. ﹣8的立方根是 , 36的平方根是 .14. 下列调查中,调查方式选择正确的是 .
①为了了解一批灯泡的使用寿命,选择抽样调查.②为了了解某公园全年的游客流量,选择抽样调查.③为了了解某1000枚炮弹的杀伤半径,选择全面调查.④为了了解一批袋装食品是否有防腐剂,选择全面调查.
15. 在两个连续整数a和b之间,a<<b,那么b﹣a的值为 .16. 点P(a,b)距离x轴2个单位长度,距离y轴3个单位长度且ab>0,则P点的坐标是 .17. 点 为线段 上一点,不与点 、 重合, 于点 ,若 ,则 的度数为 .18. 若方程是关于 , 的二元一次方程,则 .19. 若关于x的不等式2x-a≤4有3个非负整数解,则a的取值范围是 .20. 在平面直角坐标系中,对于点P(x,y),我们把点P′(-y+1,x+1)叫做点P的幸运点.已知点A1的幸运点为A2 , 点A2的幸运点为A3 , 点A3的幸运点为A4 , …,这样依次得到点A1 , A2 , A3 , …,An.若点A1的坐标为(3,1),则点A2020的坐标为 .三、解答题
-
21.(1)、计算: .(2)、解方程组(3)、解不等式组 , 并写出它的正整数解.22. 某市教育局在全市党员教职工中开展的“学党史,知党情,颂党恩”活动中,进行了论文的评比,论文的交稿时间为6月1日至25日,评委会把各校交的论文的篇数按4天一组分组统计,绘制成如图所示的频数分布直方图(每组包括左端点,不包括右端点)已知从左往右各小长方形的高的比为2:3:4:6:4:1,第二组的频数为18.请回答下列问题.
 (1)、本次活动共有多少篇论文参加评比?(2)、哪组上交的论文数量最多?是多少?(3)、经过评比,第四组和第六组分别有20篇、4篇论文获奖,则这两组哪组获奖率高?23. 如图,三角形 在平面直角坐标系中第二象限内,顶点 的坐标是 ,先把三角形 向右平移4个单位,再向下平移3个单位得到三角形 .
(1)、本次活动共有多少篇论文参加评比?(2)、哪组上交的论文数量最多?是多少?(3)、经过评比,第四组和第六组分别有20篇、4篇论文获奖,则这两组哪组获奖率高?23. 如图,三角形 在平面直角坐标系中第二象限内,顶点 的坐标是 ,先把三角形 向右平移4个单位,再向下平移3个单位得到三角形 . (1)、请在图中作出三角形 ;(2)、点 的坐标为;点 的坐标为;点 的坐标为;(3)、求三角形 的面积.24. 如图,已知 .
(1)、请在图中作出三角形 ;(2)、点 的坐标为;点 的坐标为;点 的坐标为;(3)、求三角形 的面积.24. 如图,已知 . (1)、求证:
(1)、求证:证明:(已知)
( ▲ ).
又(已知),
▲ (等量代换),
( ▲ ).
(2)、已知 , 若平分 , 求的度数.25. 为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.(1)、求购买A型和B型公交车每辆各需多少万元?(2)、预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?(3)、在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?26. 如图1,在平面直角坐标系中, ,且满足 ,过C作 轴于B. (1)、求 的面积.(2)、若过B作 交y轴于D,且 分别平分 ,如图2,求 的度数.(3)、在y轴上存在点P使得 和 的面积相等,请直接写出P点坐标.
(1)、求 的面积.(2)、若过B作 交y轴于D,且 分别平分 ,如图2,求 的度数.(3)、在y轴上存在点P使得 和 的面积相等,请直接写出P点坐标.