黑龙江省牡丹江市2020-2021学年七年级下学期期末考试数学试题
试卷更新日期:2022-04-28 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点P(﹣3,﹣5)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列命题中,真命题的是( )A、内错角都相等 B、同位角不一定相等 C、同旁内角不可能相等 D、同旁内角相等,两直线平行3. 若m>n,则下列不等式正确的是( )A、m﹣2<n﹣2 B、 C、6m<6n D、﹣8m>﹣8n4. 在“12月4日中国国家宪法日”来临之际,牡丹江市的某社区为了解该社区居民的法律意识,随机调查测试了该社区人,其中人的法律意识测试结果为合格及以上.关于以上数据的收集与整理过程,下列说法正确的是( )A、样本容量是 B、人的法律意识测试结果是总体 C、该社区只有人的法律意识不合格 D、调查的方式是抽样调查5. 为奖励消防演练中表现优异的同学,某校决定用1200元购买篮球和排球,其中篮球每个120元,排球每个90元(至少保证有个排球),在购买资金恰好用尽的情况下,购买方案有( )A、种 B、种 C、种 D、种6. 若点在轴的左侧,则下列判断正确的是( )A、 , B、 C、 , D、 ,7. 已知 是关于x、y的二元一次方程组 的解,则m+2n的值为( )A、 B、1 C、7 D、118. 某出租车起步价所包含的路程为千米,超过千米的部分按每千米另收费.成成同学乘坐这种出租车行驶了千米,付了元;盼盼同学乘坐这种出租车行驶了千米,付了元.设这种出租车的起步价为元,超过千米后每千米收费元,则可列方程组为( )A、 B、 C、 D、9. 已知关于的不等式组只有三个整数解,则的取值范围是( )A、 B、 C、 D、10. 如图, , , , 分别是 , 的平分线,于 . 下列结论:①;②;③;④平分;⑤ . 其中正确结论的个数是( )
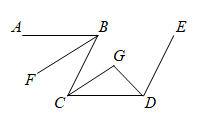 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 的平方根是 .12. 如图,直线 , 相交于点 , 于 , 交于点 , 若 , 则的度数为 .
 13. 在一个样本中,50个数据分别落在5个小组内,第1,2,3,5小组数据的频数分别是2,8,5,15,则第4个小组的频数为 .14. 已知 , 满足方程组则的值为 .15. 如图,点 , 的坐标分别为 , ,将三角形 沿 轴向右平移,得到三角形 ,已知 ,则点C的坐标为.
13. 在一个样本中,50个数据分别落在5个小组内,第1,2,3,5小组数据的频数分别是2,8,5,15,则第4个小组的频数为 .14. 已知 , 满足方程组则的值为 .15. 如图,点 , 的坐标分别为 , ,将三角形 沿 轴向右平移,得到三角形 ,已知 ,则点C的坐标为. 16. 某超市“五一房价”优惠顾客,若一次性购物不超过元不优惠,超过时按全额九折优惠.一位顾客第一次购物付款元,第二次购物付款元,若这两次购物合并成一次付款,需付款 , 则 .17. 若关于x、y的二元一次方程组的解满足>1,则k的取值范围是 .18. 在平面直角坐标系中,已知不同两点与 , 且轴, , 则的值为 .19. 小华准备用元钱同时购买甲、乙两种学习用品共件,已知甲种学习用品每件元,乙种学习用品每件元,则小华最多能购买甲种学习用品件.20. 在平面直角坐标系中, , , , , , …,按照此规律排列下去,点的坐标为 .
16. 某超市“五一房价”优惠顾客,若一次性购物不超过元不优惠,超过时按全额九折优惠.一位顾客第一次购物付款元,第二次购物付款元,若这两次购物合并成一次付款,需付款 , 则 .17. 若关于x、y的二元一次方程组的解满足>1,则k的取值范围是 .18. 在平面直角坐标系中,已知不同两点与 , 且轴, , 则的值为 .19. 小华准备用元钱同时购买甲、乙两种学习用品共件,已知甲种学习用品每件元,乙种学习用品每件元,则小华最多能购买甲种学习用品件.20. 在平面直角坐标系中, , , , , , …,按照此规律排列下去,点的坐标为 .三、解答题
-
21. 计算、解方程组、解不等式组(1)、计算:;(2)、解方程组:(3)、解不等式组:22. 如图,中, , 点在边上,于 , 点在边上,交于点 .
 (1)、如图1,当 , 平分时,求的度数;(不用写出每一步的推理原因)(2)、当 , 时,直接写出的度数.23. 已知关于 , 的方程组的解满足为非正数,不大于 .(1)、求的取值范围;(2)、求当为何整数时,不等式的解集为 .24. 如今很多初中生喜欢购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此某班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:A.白开水,B.瓶装矿泉水,C.碳酸饮料,D.非碳酸饮料.根据统计结果绘制如图所示的两幅不完整的统计图,根据统计图提供的信息,解答下列问题:
(1)、如图1,当 , 平分时,求的度数;(不用写出每一步的推理原因)(2)、当 , 时,直接写出的度数.23. 已知关于 , 的方程组的解满足为非正数,不大于 .(1)、求的取值范围;(2)、求当为何整数时,不等式的解集为 .24. 如今很多初中生喜欢购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此某班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:A.白开水,B.瓶装矿泉水,C.碳酸饮料,D.非碳酸饮料.根据统计结果绘制如图所示的两幅不完整的统计图,根据统计图提供的信息,解答下列问题: (1)、这个班级有多少名同学?并补全条形统计图和扇形统计图;(2)、若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如下表),则该班同学每天用于饮品的人均花费是多少元?
(1)、这个班级有多少名同学?并补全条形统计图和扇形统计图;(2)、若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如下表),则该班同学每天用于饮品的人均花费是多少元?饮品名称
白开水
瓶装矿泉水
碳酸饮料
非碳酸饮料
平均价格(元/每瓶)
(3)、在(2)条件下,若全校有名学生,估计全校学生每天用于购买碳酸饮料的花费是多少元?25. 某市中学生在开学前准备购买额温体温计和消毒液,已知额温体温计的单价比消毒液的单价多元,购买一批额温体温计所花费用是购买相同数量消毒液所花费用的倍.请解答下列问题:(1)、额温体温计和消毒液的单价各是多少元?(2)、该学校决定购进额温体温计和消毒液共个,且额温体温计的个数不多于个;消毒液的数量不多于额温体温计数量的倍.请求出共有哪几种购买方案;(3)、若用元购买额温体温计和消毒液,在线全部用尽且消毒液超过瓶的情况下,请直接写出有几种购买方案.26. 正方形在平面直角坐标系中的位置如图所示,轴,与轴交于点 , , 且 , 的长满足 .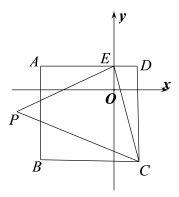 (1)、求点A的坐标;(2)、若 , 求的面积;(3)、在(2)的条件下,正方形的边上是否存在点 , 使?若存在,请直接写出点的坐标;若不存在,请说明理由.
(1)、求点A的坐标;(2)、若 , 求的面积;(3)、在(2)的条件下,正方形的边上是否存在点 , 使?若存在,请直接写出点的坐标;若不存在,请说明理由.