黑龙江省哈尔滨市松北区2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程中，是二元一次方程的是（）

A、 $2 x + \frac{1}{y} = 8$ B、 $- x^{2} + 2 y = 7$ C、 $- x + 2 = 9$ D、 $7 x - 2 y = 13$

查看试题解析
2. 如果 $x > y$ ，则下列变形中正确的是（）

A、 $- \frac{1}{2} x > - \frac{1}{2} y$ B、 $\frac{1}{2} x < \frac{1}{2} y$ C、 $3 x > 5 y$ D、 $x - 3 > y - 3$

查看试题解析
3. 下列长度的三条线段中，能组成三角形的是（）

A、 $2 c m$ ， $5 c m$ ， $7 c m$ B、 $0.1 c m$ ， $0.1 c m$ ， $0.1 c m$ C、 $8 c m$ ， $8 c m$ ， $17 c m$ D、 $7 c m$ ， $40 c m$ ， $8 c m$

查看试题解析
4. 把不等式组 ${\begin{matrix} x + 1 \geq 0 \\ 2 - x > 0 \end{matrix}$ 的解集表示在数轴上，正确的是（）

A、 B、 C、 D、

查看试题解析
5. 下面四个图形中，线段BE是⊿ABC的高的图是（）

A、 B、 C、 D、

查看试题解析
6. 一个正n边形的每个内角均为140°，则 $n =$ （）

A、6 B、7 C、8 D、9

查看试题解析
7. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 9 0^{°}$ ， $∠ A = 5 0^{°}$ ，将其折叠使点A落在BC边上的点 $A^{^{'}}$ 处，折痕为 $C D$ ，则 $∠ A^{'} D C =$ （）

A、10° B、30° C、65° D、85°

查看试题解析
8. 若不等式 $(k - 2) x > k - 2$ 的解集是 $x < 1$ ，则 $k$ 满足（）

A、 $k < 0$ B、 $k > 2$ C、 $k < 2$ D、 $k < - 2$

查看试题解析
9. 足球比赛的得分规则如下：胜一场得3分，平一场得1分，负一场得0分.某足球队一共进行了14场比赛，其中负了5场，共得19分.设该球队胜了x场，平了y场，依题意可列方程组 $()$

A、 ${\begin{array}{l} x + y + 5 = 14 \\ 3 x + y = 19 \end{array}$ B、 ${\begin{array}{l} x + y + 5 = 14 \\ x + 3 y = 19 \end{array}$ C、 ${\begin{array}{l} x + y - 5 = 14 \\ x + 3 y = 19 \end{array}$ D、 ${\begin{array}{l} x + y - 5 = 14 \\ 3 x + y = 19 \end{array}$

查看试题解析
10. 有下列说法：
⑴外角和为360°的多边形一定是三角形：
⑵有两条边分别相等的两个三角形是全等三角形；
⑶角的平分线上的点到角的两边的距离相等：
⑷如果 $∠ A = ∠ B + ∠ C$ ，那么 $△ A B C$ 是直角三角形．
其中正确的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 已知 $4 x - 2 y = 3$ ，用含 $x$ 的代数式表示 $y$ ，则 $y =$ ．

查看试题解析
12. $x$ 的3倍与7的和大于9，用不等式可表示为．

查看试题解析
13. 甲、乙两台机床生产一种零件，10天中两台机床每天生产次品的平均数都是2，方差是 ${S^{2}}_{甲} = 0.76$ ， ${S^{2}}_{乙} = 1.65$ ，两台机床出次品的波动较小的是机床．（填“甲”或“乙”）

查看试题解析
14. 若 ${\begin{array}{l} x = 2 \\ y = 5 \end{array}$ 是方程kx－2y＝2的一个解，则k的值为．

查看试题解析
15. 某公司招聘员工，公司对应聘人员进行三项测试：语言、设计和综合知识．公司将把三项测试得分按2∶3∶4的比确定每人的最后成绩，已知小王三项测试得分依次为90分、81分和72分，则他的最后成绩为分．

查看试题解析
16. 一个等腰三角形的两边长分别为3和7，这个三角形的周长是．

查看试题解析
17. 如图， $∠ A B D = 15 °$ ， $∠ A C D = 30 °$ ， $∠ A = 45 °$ ，则 $∠ B D C$ 的度数为．

查看试题解析
18. 某次知识竞赛共有20题，每一题答对得10分，答错或不答都扣5分，小明得分要超过90分，他至少答对道.

查看试题解析
19. 已知AH为 $△ A B C$ 的高，若 $∠ B = 40 ° ， ∠ A C H = 65 °$ ，则 $∠ B A C$ 的度数为．

查看试题解析
20. 如图，在 $△ A B C$ 中，点D为AC边的中点，过点C作 $C F / / A B$ ，过点D作直线EF交AB于点E，交直线CF于点F，若 $B E = 9 ， C F = 6$ ， $△ A B C$ 的面积为50，则 $△ C D F$ 的面积为．

查看试题解析

三、解答题

21. 解下列方程组及不等式组．

(1)、 ${\begin{array}{l} x - y = 3 \\ 3 x - 8 y = 14 \end{array}$

(2)、 ${\begin{array}{l} x - 3 (x - 2) > 4 \\ \frac{2 x + 1}{3} > x - 1 \end{array}$

查看试题解析
22. 如图所示方格纸中，每个小正方形的边长均为1，点 $A$ ，点 $B$ ，点 $C$ 在小正方形的顶点上．

(1)、画出 $△ A B C$ 的边 $B C$ 上的高 $A D$ ．

(2)、画出 $△ A B C$ 的边 $A C$ 上的中线 $B E$ ；

(3)、直接写出 $△ A B E$ 的面积为．

查看试题解析
23. 为了调查学生每天零花钱情况，对我校七年级某班50名同学每天零花钱情况进行了统计，并绘制成下面的统计图：

(1)、这50名同学零花钱的众数为；中位数为．

(2)、求这50名同学零花钱的平均数：

(3)、该校共有学生3000人，请你根据该班的零花钱情况，估计这所中学学生每天的零花钱总数是多少元?

查看试题解析
24. 如图，在 $△ A B C$ 中， $A B = A C$ ， $B E ⊥ A C$ 于点 $E$ ， $C F ⊥ A B$ 于点 $F$ ，且 $B E$ 与 $C F$ 相交于点 $O$ ．

(1)、求证：BF=CE；

(2)、不添加辅助线，直接写出图中所有的全等三角形．

查看试题解析
25. 学校为丰富学生的业余生活，为学生购买排球和篮球．若买10个排球和8个篮球需1600元；若买15个排球和20个篮球需3200元．

(1)、每个排球和篮球的售价分别多少元?

(2)、若学校打算购买排球和篮球共50个，购买的费用不超过4680元，则至少购买排球多少个?

查看试题解析
26. 在 $A B C △$ 中， $A B = A C$ .

(1)、如图1、求证： $∠ B = ∠ C$ ：

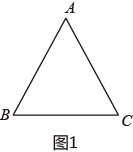
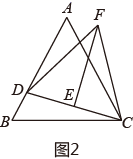
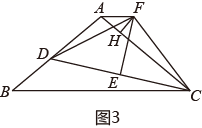(2)、如图2，D为AB上一点，连接CD，E为CD中点，过点E作 $E F ⊥ C D$ 于点E，连接 $F C ， F D$ ，求证： $F C = F D$ ；

(3)、如图3，在（2）的条件下，过点F作 $F H ⊥ A C$ 于点H，连接AF，若 AF∥BC，FH=4，CH=20，BD=10 ，求 $△ A D F$ 的面积

查看试题解析
27. 如图，在平面直角坐标系中，点 $O$ 为坐标原点，点 $A (0 ， a)$ 在 $y$ 轴正半轴上，点 $B (b ， 0)$ 在 $x$ 轴正半轴上，且 $a$ ， $b$ 是方程组 ${\begin{array}{l} 2 a - b = 8 \\ a + 2 b = 14 \end{array}$ 的解．

(1)、直接写出点A的坐标为，点B的坐标为．

(2)、动点P从点B出发，以每秒1个单位长度的速度沿射线BO方向运动，连接AP，设P点的运动时间为 $t$ 秒， $△ A O P$ 的面积为S，用含 $t$ 的式子表示S，并直接写出 $t$ 的取值范围：

(3)、在（2）的条件下，当点P在 $x$ 轴负半轴上时，且 $S = 6$ ，在 $y$ 轴负半轴上有一点C，过点B作 $x$ 轴垂线，与射线PC交于点D，若 $∠ C P O + 2 ∠ A P O = 18 0^{°} ， P D = \frac{15}{2}$ ，连接AD，交OB于点E，求点E的坐标．

查看试题解析