黑龙江省大庆市龙凤区2020-2021学年七年级下学期期末数学试题
试卷更新日期:2022-04-28 类型:期末考试
一、单选题
-
1. 下列实数中,是无理数的是( )A、 B、 C、 D、2. 下列方程组中是二元一次方程组的是( )A、 B、 C、 D、3. 下列四组数据,不是勾股数的是( )A、3,4,5 B、5,6,7 C、6,8,10 D、9,40,414. 一组数据1,1,2,3,4,4,5,6的众数是( )A、1 B、4 C、1和4 D、3.55. 在平面直角坐标系中,点P(﹣3,4)关于x轴的对称点的坐标是( )A、(﹣4,﹣3) B、(﹣3,﹣4) C、(3,4) D、(3,﹣4)6. 下列是真命题的是( )A、有一个角等于60°的三角形是等边三角形 B、在同一平面内 , , 则 C、同旁内角互补角 D、对顶角相等么?7. 正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=kx﹣k的图象大致是( )A、
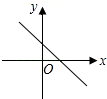 B、
B、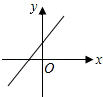 C、
C、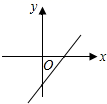 D、
D、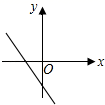 8. 已知一组数据 , , , , 的方差是3,则 , , , , 的方差是( )A、3 B、6 C、9 D、129. 如图,△CEF中,∠E=70°,∠F=50°,且AB∥CF ,AD∥CE,连接BC,CD,则∠A的度数是( )
8. 已知一组数据 , , , , 的方差是3,则 , , , , 的方差是( )A、3 B、6 C、9 D、129. 如图,△CEF中,∠E=70°,∠F=50°,且AB∥CF ,AD∥CE,连接BC,CD,则∠A的度数是( )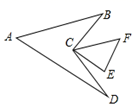 A、40° B、45° C、50° D、60°10. 已知关于x、y的二元一次方程组给出下列结论:①当k=5时,此方程组无解;②若此方程组的解也是方程6x+15y=16的解,则k=10;③无论整数k取何值,此方程组一定无整数解(x、y均为整数),其中正确的是( )A、①②③ B、①③ C、②③ D、①②
A、40° B、45° C、50° D、60°10. 已知关于x、y的二元一次方程组给出下列结论:①当k=5时,此方程组无解;②若此方程组的解也是方程6x+15y=16的解,则k=10;③无论整数k取何值,此方程组一定无整数解(x、y均为整数),其中正确的是( )A、①②③ B、①③ C、②③ D、①②二、填空题
-
11. 4的算术平方根是 .12. 平面直角坐标系中,点到x轴的距离是 .13. 已知 , 则 .14. 为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机取部分麦苗,获得苗高(单位;cm)的平均数与方差为: , ;.S甲2=S丁2=3.6,S乙2=S丙2=6.3,则麦苗又高又整齐的是.15. 如图,在 中,已知 于点 , , ,则 的度数为 .
 16. 四位同学参加数学知识竞赛活动,分别获得第一、二、三、四名,大家猜测谁得第几名时,明明说:“甲得第一,乙得第二”;文文说:“甲得第二,丁得第四”;凡凡说:“丙得第二,丁得第三”.名次公布后,他们每人都只猜对了一半,那么甲、乙、丙、丁的名次顺序为.(按一、二、三、四的名次排序)17. 已知,如图点 , , 点为轴上一点,当最大时,点的坐标为 .
16. 四位同学参加数学知识竞赛活动,分别获得第一、二、三、四名,大家猜测谁得第几名时,明明说:“甲得第一,乙得第二”;文文说:“甲得第二,丁得第四”;凡凡说:“丙得第二,丁得第三”.名次公布后,他们每人都只猜对了一半,那么甲、乙、丙、丁的名次顺序为.(按一、二、三、四的名次排序)17. 已知,如图点 , , 点为轴上一点,当最大时,点的坐标为 .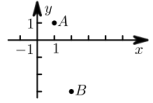 18. 已知有若干片相同的拼图,其形状如图(一)所示.当4片拼图紧密拼成一列时长度为23cm,如图(二)所示.当10片拼图紧密拼成一列时长度为56cm,如图(三)所示.则图(一)中的拼图长度为cm.
18. 已知有若干片相同的拼图,其形状如图(一)所示.当4片拼图紧密拼成一列时长度为23cm,如图(二)所示.当10片拼图紧密拼成一列时长度为56cm,如图(三)所示.则图(一)中的拼图长度为cm.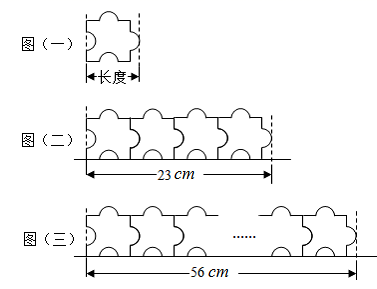
三、解答题
-
19.(1)、(2)、20.(1)、(2)、21. 《九章算术》中的“引葭赴岸”问题:今有池方一丈,葭(一种芦苇类植物)生其中央,出水一尺.引葭赴岸,适与岸齐,水深几何?其大意是:有一个边长为10尺的正方形池塘,一棵芦苇生长在它的正中央,高出水面1尺.如果把该芦苇拉向岸边,那么芦苇的顶部恰好碰到岸边(如图所示),则水深多少尺.
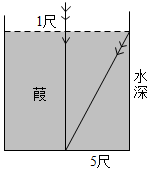 22. 已知点 .(1)、当点在轴上时,求点的坐标;(2)、点到轴、轴的距离相等,求点的坐标.23. (如图所示,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并对结论进行说理。
22. 已知点 .(1)、当点在轴上时,求点的坐标;(2)、点到轴、轴的距离相等,求点的坐标.23. (如图所示,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并对结论进行说理。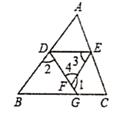 24. 甲、乙两教师参加“学习强国”争上游比赛.每局10道题目,各自连续做10局,每局做对的题目的个数被记录下来制成了下面的统计图:
24. 甲、乙两教师参加“学习强国”争上游比赛.每局10道题目,各自连续做10局,每局做对的题目的个数被记录下来制成了下面的统计图: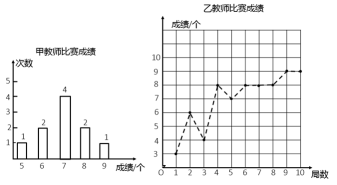
根据以上信息,整理分析数据如表:
平均成绩/个
中位数/个
众数/个
甲
7
乙
7
8
(1)、表格中 , , 的值分别是: , , ;(2)、甲、乙两位教师成绩较稳定的是哪位教师呢,请说明理由.25. 在2020年双11到来之前,某商家为了囤货,投入28000元资金购进 、 两种商品共1000件,两种商品的成本价和销售价如下表所示:商品
单价(元/件)
成本价
销售价
25
35
30
45
(1)、该商家购进两种商品各多少件?(2)、这批商品全部销售完后,该商家共获利多少元?26. 如图1,已知直线与x轴交于点A,与y轴交于点B,直线l2与y轴交于点 , 与直线l1交于点D(2,t).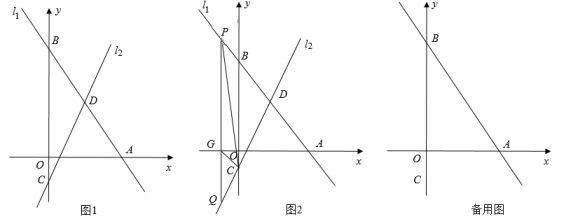 (1)、求直线l2的解析式;(2)、如图2,若点P在直线l1上,过点P作轴交l2于点Q,交x轴于点G,使 , 求此时P点的坐标;(3)、将直线向左平移10个单位得到直线l3交x轴于点E,点F是点C关于原点的对称点,过点F作直线轴.在直线l4上是否存在动点M,使得为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
(1)、求直线l2的解析式;(2)、如图2,若点P在直线l1上,过点P作轴交l2于点Q,交x轴于点G,使 , 求此时P点的坐标;(3)、将直线向左平移10个单位得到直线l3交x轴于点E,点F是点C关于原点的对称点,过点F作直线轴.在直线l4上是否存在动点M,使得为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.