高中数学人教A版（2019）选修三第六章计数原理

试卷更新日期：2022-04-27 类型：期中考试

进入出卷网下载

一、单选题

1. 为弘扬我国古代的“六艺”文化，某小学开设“礼”“乐”“射”“御”“书”“数”六门体验课程，每周一门，连续开设六周，课程“乐”“数”排在相邻两周，则不同的安排方案有（）

A、60种 B、120种 C、240种 D、480种

查看试题解析
2. 在“志愿和平”活动中，某校高二年级3名男教师和4名女教师参与社区防控新冠肺炎疫情的志愿服务.根据岗位需求应派3人巡视商户，且至少有1名男教师；另外4人测量出入人员体温.则这7名教师不同的安排方法有（）

A、15种 B、18种 C、31种 D、45种

查看试题解析
3. 在 ${(\frac{1}{x} - x^{2})}^{6}$ 的展开式中 $x^{6}$ 的系数是（）

A、-20 B、-15 C、20 D、15

查看试题解析
4. 把1，2，3，4，5这五个数随机排成一列，组成一个数列，要求该数列恰好先减后增，则这样的数列有（）

A、13个 B、14个 C、15个 D、16个

查看试题解析
5. 甲乙丙三名高一学生都已选择物理、化学两科作为自己的高考科目，三人独自决定从政治、历史、地理、生物、技术中任选一科作为自己的第三门高考选考科目，则不同的选法种数为（）

A、 $A_{5}^{3}$ B、 $3 C_{5}^{1}$ C、 $3^{5}$ D、 $5^{3}$

查看试题解析
6. 第24届冬季奥运会将于2022年2月4日至2022年2月20日在北京市和河北省张家口市举行．现要安排甲、乙、丙、丁四名志愿者去国家高山滑雪馆、国家速滑馆、首钢滑雪大跳台三个场馆参加活动，要求每个场馆都有人去，且这四人都在这三个场馆，则甲和乙都没被安排去首钢滑雪大跳台的种数为（）

A、12 B、14 C、16 D、18

查看试题解析
7. 在 ${(3 x^{3} - 5 x^{2} + 1)}^{5}$ 的展开式中，除 $x^{5}$ 项之外，剩下所有项的系数之和为（）

A、299 B、-301 C、300 D、-302

查看试题解析
8. 已知 ${(2 x - 1)}^{4} + {(x + 1)}^{3} = a_{4} x^{4} + a_{3} x^{3} + a_{2} x^{2} + a_{1} x + a_{0}$ ，则 $a_{2} =$ （）

A、9 B、24 C、27 D、33

查看试题解析

二、多选题

9. 有4名男生、3名女生，在下列不同条件下，不同的排列方法数正确的是（）

A、排成前后两排，女生排前排，男生排后排，共有 $A_{3}^{3} \times A_{4}^{4}$ 种方法 B、全体排成一排，男生互不相邻，共有 $A_{3}^{3} \times A_{4}^{4}$ 种方法 C、全体排成一排，女生必须站在一起，共有 $3 A_{5}^{5}$ 种方法 D、全体排成一排，其中甲不站在最左边，乙不站在最右边，共有 $A_{7}^{7} - 2 A_{6}^{6}$ 种方法

查看试题解析
10. 在10件产品中，有7件合格品，3件不合格品，从这10件产品中任意抽出3件，则下列结论正确的有（）

A、抽出的3件产品中恰好有1件是不合格品的抽法有 $C_{3}^{1} C_{7}^{2}$ 种 B、抽出的3件产品中至少有1件是不合格品的抽法有 $C_{3}^{1} C_{9}^{2}$ 种 C、抽出的3件产品中至少有1件是不合格品的抽法有 $C_{3}^{1} C_{7}^{2} + C_{3}^{2} C_{7}^{1} + C_{3}^{3}$ 种 D、抽出的3件产品中至少有1件是不合格品的抽法有 $C_{10}^{3} - C_{7}^{3}$ 种

查看试题解析
11. “杨辉三角”是中国古代数学杰出的研究成果之一.如图所示，由杨辉三角的左腰上的各数出发，引一组平行线，从上往下每条线上各数之和依次为 $1 ， 1 ， 2 ， 3 ， 5 ， 8 ， 13 ， \dots$ ，则（）

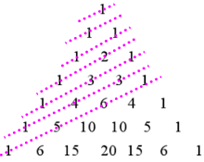A、在第9条斜线上，各数之和为55 B、在第 $n (n \geq 5)$ 条斜线上，各数自左往右先增大后减小 C、在第n条斜线上，共有 $\frac{2 n + 1 - {(- 1)}^{n}}{4}$ 个数 D、在第11条斜线上，最大的数是 $C_{7}^{3}$

查看试题解析
12. 若 ${(2 - 3 x)}^{2021} = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + ⋯ + a_{2020} x^{2020} + a_{2021} x^{2021}$ ，则正确的是（）

A、 $a_{0} = 2$ B、 $a_{1} + a_{3} + a_{5} + ⋯ + a_{2019} + a_{2021} = \frac{- 1 - 5^{2021}}{2}$ C、 $| a_{0} | + | a_{1} | + | a_{2} | + ⋯ + | a_{2021} | = 5^{2021}$ D、 $\frac{a_{1}}{2} + \frac{a_{2}}{2^{2}} + \frac{a_{3}}{2^{3}} + ⋯ + \frac{a_{2020}}{2^{2020}} + \frac{a_{2021}}{2^{2021}} = {(\frac{1}{2})}^{2021}$

查看试题解析

三、填空题

13. 已知 $(x^{2} + a) {(\frac{1}{x^{2}} + 1)}^{5}$ 的展开式中的常数项为8，则 $a =$ .

查看试题解析
14. ${(1 + x)}^{5} {(1 - x)}^{4}$ 的展开式中 $x^{2}$ 的系数为．

查看试题解析
15. 已知 $(1 + x) {(2 - x)}^{4} = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + a_{4} x^{4} + a_{5} x^{5}$ ，则 $a_{3} =$ ．

查看试题解析
16. 2022年北京冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”，有着可爱的外表和丰富的寓意，深受各国人民的喜爱.某商店有4个不同造型的“冰墩墩”吉祥物和3个不同造型的“雪容融”吉祥物展示在柜台上，要求“冰墩墩”和“雪容融”彼此间隔排列，则不同的排列方法种数为.（用数字作答）

查看试题解析

四、解答题

17. 已知 ${(x - \frac{1}{2 \sqrt{x}})}^{n}$ 的展开式中所有项的系数之和为 $\frac{1}{256}$ .

(1)、求展开式中 $\frac{1}{x}$ 的系数；

(2)、从展开式的所有项中任取两项，求这两项中至少有一项是有理项（x的指数为整数）的概率.

查看试题解析
18. 现有高二4个班的学生34人，其中一、二、三、四班各7、8、9、10人，他们自愿组成数学课外小组.

(1)、选其中一人为负责人，有多少种不同的选法？

(2)、每班选一名组长，有多少种不同的选法？

(3)、推选二人作中心发言，这两人需来自不同的班级，有多少种不同的选法？

查看试题解析
19. 设 ${(1 - 2 x)}^{100} = a_{0} + a_{1} x + a_{2} x^{2} + \cdot \cdot \cdot + a_{100} x^{100} (x \in R)$ ．

(1)、求 $a_{0} + a_{1} + a_{2} + \cdot \cdot \cdot + a_{100}$ 的值；

(2)、求 $a_{1} + a_{3} + a_{5} + \cdot \cdot \cdot + a_{99}$ 的值；

(3)、求 $| a_{0} | + | a_{1} | + | a_{2} | + \cdot \cdot \cdot + | a_{100} |$ 的值．

查看试题解析
20. 从 $A ， B ， C$ 等7人中选5人排成一排（以下问题均用数字作答）

(1)、若 $A$ 必须在内，有多少种排法？

(2)、若 $A ， B ， C$ 三人不全在内，有多少种排法？

(3)、若 $A ， B ， C$ 都在内，且 $A ， B$ 必须相邻， $C$ 与 $A ， B$ 都不相邻，有多少种排法？

查看试题解析
21. 高二年级线上学习至今，每个班的家长都积极配合，参与到班级管理当中，若某班某一天共有7位家长报名参与到当天的早读、上午课堂、下午课堂、晚修的管理，其中2位家长被安排管理早读，其余5位家长被安排到上午课堂、下午课堂、晚修三个时段管理.

(1)、从7位家长中安排2人参与早读管理，共有多少种不同方法；

(2)、将剩下的5位家长被安排到上午课堂、下午课堂、晚修三个时段管理，要求每个时段至少有1人，共有多少种不同安排方法；

(3)、线上学习结束后，班主任为了感谢这7位家长，召开线上会议（腾讯会议）对家长表示感谢，若7位家长先后进入会议，A、B两位家长相邻进入会议，且都不是第一个，也不是最后一个进入会议，问这7位家长进入会议时间的不同排序方式有多少种.

查看试题解析
22. 在二项式 ${(\sqrt{x} - \frac{2}{x})}^{n}$ 的展开式中，____．给出下列条件：
①若展开式前三项的二项式系数的和等于37；
②若展开式中第3项与第2项的二项式系数之比为7：2；
③所有偶数项的二项式系数的和为128．
试在上面三个条件中选择一个补充在上面的横线上，并且完成下列问题：

(1)、求 ${(\sqrt{x} - \frac{2}{x})}^{n}$ 展开式中x的系数；

(2)、写出 ${(\sqrt{x} - \frac{2}{x})}^{n}$ 展开式中二项式系数最大的项（不需要说明理由）．
注：如果选择多个条件分别解答，按第一个解答计分．

查看试题解析

高中数学人教A版（2019） 选修三 第六章 计数原理

一、单选题

二、多选题

三、填空题

四、解答题

高中数学人教A版（2019）选修三第六章计数原理