陕西省宝鸡市陈仓区2020-2021学年高一下学期数学期末考试试卷（必修3）

试卷更新日期：2022-04-27 类型：期末考试

进入出卷网下载

一、单选题

1. 种植某种花的球根200个，进行调查发芽天数的试验，样本是（）

A、200个球根发芽天数的数值 B、200个球根 C、无数个球根发芽天数的数值集合 D、无法确定

查看试题解析
2. 滴滴公司为了调查消费者对滴滴出行的真实评价，采用分层抽样的方法在甲、乙、丙三个城市共抽取了3600人进行问卷调查，若在甲、乙、丙三个城市抽取的人数分别为a，b，c，且满足 $a + c = 2 b$ ，则乙城市抽取的人数为（）

A、800 B、1000 C、1200 D、1500

查看试题解析
3.
如图，正方形ABCD内的图形来自中国古代的太极图，正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称．在正方形内随机取一点，则此点取自黑色部分的概率是（　　）

A、 $\frac{1}{4}$ B、 $\frac{π}{8}$ C、 $\frac{1}{2}$ D、 $\frac{π}{4}$

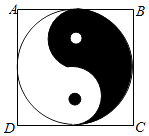查看试题解析
4. 现有60瓶饮料，编号从1到60，若用系统抽样的方法从中抽取6瓶进行检验，则所抽取的编号可能为（）

A、3，13，23，33，43，53 B、2，14，26，38，40，52 C、5，8，31，36，48，54 D、5，10，15，20，25，30

查看试题解析
5. 已知一组数据为20，30，40，50，50，60，70，80，其中平均数、中位数和众数的大小关系是（）

A、平均数>中位数>众数 B、平均数<中位数<众数 C、中位数<众数<平均数 D、众数=中位数=平均数

查看试题解析
6.
执行如图所示的程序框图，输出的S值为（　　）

A、2 B、 $\frac{3}{2}$ C、 $\frac{5}{3}$ D、 $\frac{8}{5}$

查看试题解析
7. 下面的事件：
①袋中有2个红球，4个白球，从中任取3个球，至少取到1个白球；②某人买彩票中奖；③非零实系数一次方程必有一实根；④明天会下雨．
其中是必然事件的有（）

A、① B、④ C、① ③ D、① ④

查看试题解析
8. 甲、乙两位同学各自独立地解答同一个问题，他们能够正确解答该问题的概率分别是 $\frac{2}{5}$ 和 $\frac{1}{2}$ ，在这个问题已被正确解答的条件下，甲、乙两位同学都能正确回答该问题的概率为（）

A、 $\frac{2}{7}$ B、 $\frac{1}{5}$ C、 $\frac{2}{9}$ D、 $\frac{9}{10}$

查看试题解析
9. 当 $a = 1$ ， $b = 3$ 时，执行完如图所示的一段程序后x的值是（）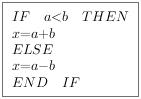

A、1 B、-2 C、3 D、4

查看试题解析
10. 在新冠肺炎疫情防控期间，某超市开通网上销售业务，每天能完成1200份订单的配货，由于订单量大幅增加，导致订单积压.为解决困难，许多志愿者踊跃报名参加配货工作.已知该超市某日积压500份订单未配货，预计第二天的新订单超过1600份的概率为0.05，志愿者每人每天能完成50份订单的配货，为使第二天完成积压订单及当日订单的配货的概率不小于0.95，则至少需要志愿者（）

A、10名 B、18名 C、24名 D、32名

查看试题解析
11. 小敏打开计算机时，忘记了开机密码的前两位，只记得第一位是M，I，N中的一个字母，第二位是1，2，3，4，5中的一个数字，则小敏输入一次密码能够成功开机的概率是（　　）

A、 $\frac{8}{15}$ B、 $\frac{1}{8}$ C、 $\frac{1}{15}$ D、 $\frac{1}{30}$

查看试题解析
12. 在区间 $[0 ， 2]$ 上随机地取一个数 $x$ ，则事件“ $- 1 \leq \log_{\frac{1}{2}} (x + \frac{1}{2} \leq 1)$ ”发生的概率为( )

A、 $\frac{3}{4}$ B、 $\frac{2}{3}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析

二、填空题

13. 将一颗质地均匀的正方体骰子先后抛掷2次，观察向上的点数，则点数和为5的概率是.

查看试题解析
14. 如图是一个算法流程图，若输出y的值为-2，则输入x的值是.

查看试题解析
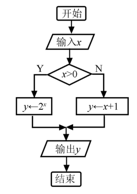15. 有A、B、C三种零件，分别为a个、300个、200个，采用分层抽样法抽取一个容量为45的样本，A种零件被抽取20个，则 $a =$ ．

查看试题解析
16. 我国古代数学名著《数书九章》有“米谷粒分”题：粮仓开仓收粮，有人送来1534石，验得米内夹谷，抽样取米一把，数得254粒内夹谷28粒，则这批米内夹谷约为．

查看试题解析

三、解答题

17. 农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况，从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高，数据如下：单位：（cm）
甲：9，10，11，12，10，20
乙：8，14，13，10，12，21．
分别计算所抽取的甲、乙两种麦苗株高的平均数与方差，并由此判断甲、乙两种麦苗的长势情况．

查看试题解析
18. 某次运动会要从甲、乙两位射击选手中选出 $1$ 名选手参加比赛，甲、乙两位射击选手分别射击了 $7$ 次，所得的成绩（环数）如下表：
甲
5
6
7
9
9
9
10
乙
4
6
5
7
8
10
9

(1)、分别写出甲选手成绩（环数）的众数和乙选手成绩（环数）的中位数；

(2)、分别求出甲、乙两位选手成绩（环数）的平均数；

(3)、根据（2）问数据，你认为选哪一位选手参加比赛更合适，并说明理由．

查看试题解析
19. 20名学生某次数学考试成绩(单位：分)的频率分布直方图如下：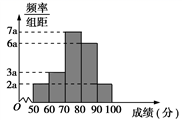

(1)、求频率直方图中a的值；

(2)、分别求出成绩落在[50，60)与[60，70)中的学生人数；

(3)、从成绩在[50，70)的学生中人选2人，求这2人的成绩都在[60，70)中的概率．

查看试题解析
20. 2020年新型冠状病毒席卷全球，美国是疫情最严重的国家，截止2020年6月8日美国确诊病例约为200万人，经过随机抽样，从感染人群中抽取1000人进行调查，按照年龄得到如下频数分布表：
年龄（岁）
$[0 ， 20)$
$[20 ， 40)$
$[40 ， 60)$
$[60 ， 80)$
$[80 ， 100)$
频数
50
a
320
300
80
（Ⅰ）求a的值及这1000例感染人员的年龄的平均数；（同一组中的数据用该组区间的中点值作代表）
（Ⅱ）用频率估计概率，求感染人群中年龄不小于60岁的概率.

查看试题解析
21. 去年5月，中央开始鼓励“地摊经济”，随即地摊在全国遍地开花.某地政府组织调研本地地摊经济，随机选取100名摊主了解他们每月的收入情况，并按收入 $($ 单位：千元 $)$ 将摊主分成六个组 $[10 ， 15)$ ， $[15 ， 20)$ ， $[20 ， 25) ， [25$ ， $30)$ ， $[30 ， 35)$ ， $[35 ， 40)$ 得到如下频率分布直方图：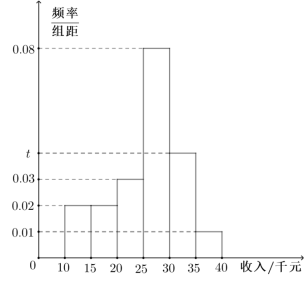

(1)、求频率分布直方图中t的值，并估计每月每名摊主收入的中位数和平均数 $($ 单位：千元 $)$ ；

(2)、已知从收入在 $[15 ， 25)$ 的摊主中用分层抽样抽取5人，现从这5人中随机抽取2人，求抽出的2 人收入都来自 $[20 ， 25)$ 的概率.

查看试题解析
22. 在全球抗击新冠肺炎疫情期间，我国医疗物资生产企业加班加点生产口罩､防护服､消毒水等防疫物品，保障抗疫一线医疗物资供应，在国际社会上赢得一片赞誉.我国某口罩生产企业在加大生产的同时，狠抓质量管理，不定时抽查口罩质量，该企业质检人员从所生产的口罩中随机抽取了100个，将其质量指标值分成以下六组： $[40 ， 50)$ ， $[50 ， 60)$ ， $[60 ， 70)$ ， …， $[90 ， 100]$ ，得到如下频率分布直方图.

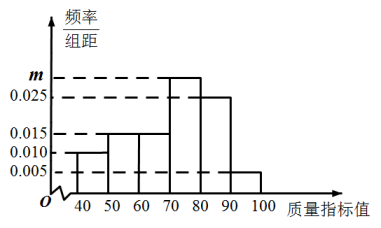(1)、求出直方图中m的值；

(2)、利用样本估计总体的思想，估计该企业所生产的口罩的质量指标值的平均数和中位数(同一组中的数据用该组区间中点值作代表，中位数精确到0.01).

查看试题解析

年龄（岁）	$[0 ， 20)$	$[20 ， 40)$	$[40 ， 60)$	$[60 ， 80)$	$[80 ， 100)$
频数	50	a	320	300	80

甲	5	6	7	9	9	9	10
乙	4	6	5	7	8	10	9