广东省广州市白云区、海珠区2020-2021学年高一下学期数学期末考试试卷

试卷更新日期：2022-04-27 类型：期末考试

进入出卷网下载

一、单选题

1. 若复数 $z = \frac{1}{3 - 4 i}$ （ $i$ 为虚数单位），则 $| z | =$ （）

A、 $\frac{1}{5}$ B、1 C、5 D、 $\frac{3}{5}$

查看试题解析
2. 已知向量 $\vec{a} = (2 ， 3)$ ， $\vec{b} = (x ， - 6)$ ，且 $\vec{a} ⊥ \vec{b}$ ，则 $x =$ （）

A、-9 B、9 C、-4 D、4

查看试题解析
3. 高一年级有男生510人，女生490人，小明按男女比例进行分层随机抽样，总样本量为100.则在男生中抽取的样本量为（）

A、48 B、51 C、50 D、49

查看试题解析
4. 如图， $△ A^{'} B^{'} C^{'}$ 是水平放置的 $△ A B C$ 的斜二测直观图， $△ A^{'} B^{'} C^{'}$ 为等腰直角三角形，其中 $O^{'}$ 与 $A^{'}$ 重合， $A^{^{'}} B^{^{'}} = 6$ ，则 $△ A B C$ 的面积是（）

A、9 B、 $9 \sqrt{2}$ C、18 D、 $18 \sqrt{2}$

查看试题解析
5. 已知 $| \vec{a} | = 6$ ， $| \vec{b} | = 4$ ， $\vec{a}$ 与 $\vec{b}$ 的夹角为 $6 0^{∘}$ ，则 $(\vec{a} + 2 \vec{b}) \cdot (\vec{a} - 3 \vec{b}) =$ （）

A、-72 B、72 C、84 D、-84

查看试题解析
6. 某学校开展“学党史，颂党恩，跟党走”学习活动，刘老师去购书中心购买了一批书籍作为阅读学习之用，其中一类是4本不同的红色经典小说类书籍，另一类是2本不同的党史类书籍，两类书籍合计共6本.现刘老师从这6本书中随机抽取2本阅读，则这两本书恰好来自同一类书籍的概率是（）

A、 $\frac{1}{15}$ B、 $\frac{2}{15}$ C、 $\frac{7}{15}$ D、 $\frac{8}{15}$

查看试题解析
7. 如图，已知 $\vec{O A} = \vec{a}$ ， $\vec{O B} = \vec{b}$ ，任意点 $M$ 关于点 $A$ 的对称点为 $S$ ，点 $M$ 关于点 $B$ 的对称点为 $N$ ，则向量 $\vec{N S} =$ （）

A、 $\frac{1}{2} (\vec{a} + \vec{b})$ B、 $2 (\vec{a} + \vec{b})$ C、 $\frac{1}{2} (\vec{a} - \vec{b})$ D、 $2 (\vec{a} - \vec{b})$

查看试题解析
8. 已知图1是棱长为1的正六边形 $A B C D E F$ ，将其沿直线 $F C$ 折叠成如图2的空间图形 $F^{'} A^{'} E^{'} - C^{'} B^{'} D^{'}$ ，其中 $A^{'} E^{'} = \frac{\sqrt{6}}{2}$ ，则空间几何体 $F^{'} A^{'} E^{'} - C^{'} B^{'} D^{'}$ 的体积为（）

A、 $\frac{3}{8}$ B、 $\frac{7}{16}$ C、 $\frac{1}{2}$ D、 $\frac{7}{8}$

查看试题解析

二、多选题

9. 某士官参加军区射击比赛，打了6发子弹，报靶数据如下：7，8，9，10，6，8，（单位：环），下列说法正确的有（）

A、这组数据的平均数是8 B、这组数据的极差是4 C、这组数据的中位数是8.5 D、这组数据的方差是2

查看试题解析
10. 已知复数 $z = c o s α + (\sqrt{3} s i n α) i$ $(α \in R)$ （ $i$ 为虚数单位），下列说法正确的有（）

A、当 $α = - \frac{π}{3}$ 时，复平面内表示复数 $z$ 的点位于第二象限 B、当 $α = \frac{π}{2}$ 时， $z$ 为纯虚数 C、 $| z |$ 最大值为 $\sqrt{3}$ D、 $z$ 的共轭复数为 $z = - c o s α + (\sqrt{3} s i n α) i$ $(α \in R)$

查看试题解析
11. 某班级到一工厂参加社会实践劳动，加工出如图所示的圆台 $O_{1} O_{2}$ ，在轴截面 $A B C D$ 中， $A B = A D = B C = 2 c m$ ，且 $C D = 2 A B$ ，下列说法正确的有（）

A、该圆台轴截面 $A B C D$ 面积为 $3 \sqrt{3} c m^{2}$ B、该圆台的体积为 $\frac{7 \sqrt{3} π}{3} c m^{3}$ C、该圆台的母线AD与下底面所成的角为30° D、沿着该圆台表面，从点C到AD中点的最短距离为 $5 c m$

查看试题解析
12. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ，点 $O$ 为 $△ A B C$ 所在平面内点，满足 $x \vec{O A} + y \vec{O B} + z \vec{O C} = 0$ ，下列说法正确的有（）

A、若 $x = y = z = 1$ ，则点 $O$ 为 $△ A B C$ 的重心 B、若 $x = y = z = 1$ ，则点 $O$ 为 $△ A B C$ 的外心 C、若 $x = a$ ， $y = b$ ， $z = c$ ，则点 $O$ 为 $△ A B C$ 的内心 D、若 $x = a$ ， $y = b$ ， $z = c$ ，则点 $O$ 为 $△ A B C$ 的垂心

查看试题解析

三、填空题

13. 有10种不同的零食，每100克可食部分包含的能量（单位：k）如下：
100，120，125，165，430，190，175，234，425，310
这10种零食每100克可食部分的能量的第60百分位数为.

查看试题解析
14. 天气预报，在元旦假期甲地降雨概率是0.2，乙地降雨概率是0.3.假设在这段时间内两地是否降雨相互之间没有影响，则这两地中恰有一个地方降雨的概率为．

查看试题解析
15. 如图，在三棱锥 $V - A B C$ 中， $V A = V B = A B = A C = B C = 4$ ， $V C = 2$ ，则二面角 $A - V C - B$ 的余弦值为.

查看试题解析
16. 如图， $△ A B C$ 是边长为1的正三角形， $M$ ， $N$ 分别为线段 $A C$ ， AB上一点，满足 $A M ： M C = 1 ： 2$ ， $A N ： N B = 1 ： 3$ ， $C N$ 与 $B M$ 的交点为 $P$ ，则线段 $A P$ 的长度为.

查看试题解析

四、解答题

17. 现有两个红球（记为 $R_{1}$ ， $R_{2}$ ），两个白球（记为 $W_{1}$ ， $W_{2}$ ），采用不放回简单随机抽样从中任意抽取两球.

(1)、写出试验的样本空间；

(2)、求恰好抽到一个红球一个白球的概率.

查看试题解析
18. 已知角 $A$ 是 $△ A B C$ 的内角，若 $\vec{a} = (\sqrt{3} s i n A ， c o s A)$ ， $\vec{b} = (1 ， - 1)$ .

(1)、若 $\vec{a} ∥ \vec{b}$ ，求角A的值；

(2)、设 $f (x) = \vec{a} \cdot \vec{b}$ ，当 $f (x)$ 取最大值时，求 $\vec{a}$ 在 $\vec{b}$ 上的投影向量（用坐标表示）.

查看试题解析
19. 如图，直三棱柱 $A B C - A^{'} B^{'} C^{'}$ 中， $D$ 是 $A B$ 的中点.

(1)、求证：直线 $B C^{'} / /$ 平面 $A^{^{'}} C D$ ；

(2)、若 $A C = C B$ ，求异面直线 $A B^{'}$ 与 $C D$ 所成角的大小.

查看试题解析
20. 2021年五一假期，各高速公路车流量大，交管部门在某高速公路区间测速路段随机抽取40辆汽车进行车速调查，将这40辆汽车在该区间测速路段的平均车速 $(k m / h)$ 分成六段 $[90 ， 95)$ ， $[95 ， 100)$ ， $[100 ， 105)$ ， $[105 ， 110)$ ， $[110 ， 115)$ ， $[115 ， 120]$ ，得到如图的频率分布直方图.

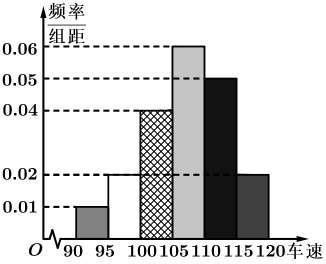(1)、根据频率分布直方图估计出这40辆汽车的平均车速的中位数；

(2)、现从平均车速在区间 $[90 ， 100)$ 的车辆中任意抽取2辆汽车，求抽取的2辆汽车的平均车速都在区间 $[95 ， 100)$ 上的概率；

(3)、出于安全考虑，测速系统对平均车速在区间 $[115 ， 120]$ 的汽车以实时短信形式对车主进行安全提醒，确保行车安全.假设每辆在此区间测速路段行驶的汽车平均车速相互不受影响，以此次调查的样本频率估计总体概率，求连续2辆汽车都收到短信提醒的概率？

查看试题解析
21. 如图， $P A$ 垂直于 $⊙ O$ 所在的平面， $A C$ 为 $⊙ O$ 的直径， $A B = 3$ ， $B C = 4$ ， $P A = 3 \sqrt{2}$ ， $A E ⊥ P B$ ，点 $F$ 为线段 $B C$ 上一动点.

(1)、证明：平面 $A E F ⊥$ 平面 $P B C$ ；

(2)、当点F移动到 $C$ 点时，求PB与平面AEF所成角的正弦值.

查看试题解析
22. 为响应国家“乡村振兴”号召，农民王大伯拟将自家一块直角三角形地按如图规划成3个功能区： $△ B N C$ 区域为荔枝林和放养走地鸡， $△ C M A$ 区域规划为“民宿”供游客住宿及餐饮， $△ M N C$ 区域规划为小型鱼塘养鱼供休闲垂钓.为安全起见，在鱼塘 $△ M N C$ 周围筑起护栏.已知 $A C = 40 m$ ， $B C = 40 \sqrt{3} m$ ， $A C ⊥ B C$ ， $∠ M C N = 30 °$ .

(1)、若 $A M = 20 m$ 时，求护栏的长度（ $△ M N C$ 的周长）；

(2)、若鱼塘 $△ M N C$ 的面积是“民宿” $△ C M A$ 的面积的 $\frac{\sqrt{6}}{2}$ 倍，求 $∠ A C M$ ；

(3)、当 $∠ A C M$ 为何值时，鱼塘 $△ M N C$ 的面积最小，最小面积是多少？

查看试题解析