安徽省六安市舒城县2020-2021学年高一下学期数学期末考试试卷

试卷更新日期：2022-04-27 类型：期末考试

进入出卷网下载

一、单选题

1. 若复数z满足 $i \cdot z = 2 - i$ ，则 $| z | =$ （）

A、1 B、2 C、 $\sqrt{3}$ D、 $\sqrt{5}$

查看试题解析
2. 从6个篮球、2个排球中任选3个球，则下列事件中，是必然事件的是（）

A、3个都是篮球 B、至少有1个是排球 C、3个都是排球 D、至少有1个是篮球

查看试题解析
3. 已知在平行四边形ABCD中，点M、N分别是BC、CD的中点，如果 $\vec{A B}$ = $\vec{a}$ ， $\vec{A D}$ = $\vec{b}$ ，那么向量 $\vec{M N}$ =（）

A、 $\frac{1}{2} \vec{a} - \frac{1}{2} \vec{b}$ B、 $- \frac{1}{2} \vec{a} + \frac{1}{2} \vec{b}$ C、 $\vec{a} + \frac{1}{2} \vec{b}$ D、 $- \frac{1}{2} \vec{a} - \frac{1}{2} \vec{b}$

查看试题解析
4. 某学校对甲、乙两个班级的某次成绩进行统计分析，制成了如图的条形图与扇形图，则下列说法一定正确的是（）

A、甲班成绩优良人数超过了乙班成绩优良人数 B、甲班平均成绩高于乙班平均成绩 C、甲班学生比乙班学生发挥稳定 D、甲班不及格率高于乙班不及格率

查看试题解析
5. 口袋中有100个大小相同的红球、白球、黑球，其中红球32个，从口袋中摸出一个球，摸出白球的概率为0.23，则摸出黑球的概率为（）

A、0.32 B、0.45 C、0.64 D、0.67

查看试题解析
6. 已知圆锥的表面积为3π，它的侧面展开图是一个半圆，则此圆锥的体积为（）

A、 $\sqrt{3} π$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{3}}{3} π$ D、 $\sqrt{3}$

查看试题解析
7. 设m，n是两条不同直线， $α$ ， $β$ 是两个不同平面，则下列说法错误的是（）

A、若 $m ⊥ α$ ， $n ⊥ α$ ，则 $m / / n$ ； B、若 $α / / β$ ， $m ⊥ α$ ，则 $m ⊥ β$ ； C、若 $m / / α$ ， $n / / α$ ，则 $m / / n$ ； D、若 $m ⊥ α$ ， $m / / β$ ，则 $α ⊥ β$ ．

查看试题解析
8. “幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标，常用区间[0,10]内的一个数来表示，该数越接近10表示满意度越高.现随机抽取10位嘉祥县居民，他们的幸福感指数为 3，4，5，5，6，7，7，8，9，10.则这组数据的 80%分位数是（）

A、7.5 B、8 C、8.5 D、9

查看试题解析
9. 若 $(a + b + c) (b + c - a) = 3 b c$ ，且 $\sin A = 2 \sin B \cos C$ ，那么 $△ A B C$ 是（）

A、直角三角形 B、等边三角形 C、等腰三角形 D、等腰直角三角形

查看试题解析
10. 如图，在正方形 $A B C D$ 中， $A B = 2$ ，E为 $B C$ 的中点，点P是以 $A B$ 为直径的圆弧上任一点．则 $\vec{A E} \cdot \vec{A P}$ 的最大值为（）

A、4 B、5 C、 $2 \sqrt{5}$ D、 $2 + \sqrt{5}$

查看试题解析
11. 连掷一枚均匀的骰子两次，所得向上的点数分别为m，n，记 $t = m + n$ ，则下列说法正确的是（）

A、事件“ $t = 12$ ”的概率为 $\frac{1}{21}$ B、事件“t是奇数”与“m=n”互为对立事件 C、事件“ $t = 2$ ”与“ $t \neq 3$ ”互为互斥事件 D、事件“ $t > 8$ 且 $m n < 32$ ”的概率为 $\frac{1}{4}$

查看试题解析
12. 如图，ABCD是边长为2的正方形，点E，F分别为边BC，CD的中点，将△ABE，△ECF，△FDA分别沿AE，EF，FA折起，使B，C，D三点重合于点P，则下列结论错误的是（）

A、AP⊥EF B、点P在平面AEF内的射影为△AEF的垂心 C、二面角A－EF－P的余弦值为 $\frac{1}{3}$ D、若四面体P－AEF的四个顶点在同一个球面上，则该球的表面积是24 $π$

查看试题解析

二、填空题

13. 天气预报说，在今后的三天中，每一天下雨的概率均为 $40 %$ ．现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率：先利用计算器产生0到9之间取整数值的随机数，用1，2，3，4表示下雨，用5，6，7，8，9，0表示不下雨；再以每三个随机数作为一组，代表这三天的下雨情况．经随机模拟试验产生了如下20组随机数：
488 932 812 458 989 431 257 390 024 556

734 113 537 569 683 907 966 191 925 271

据此估计，这三天中恰有两天下雨的概率近似为.

查看试题解析
14. 已知 $| \vec{a} | = 3$ ， $\vec{e} = (1 ， 0)$ ，向量 $\vec{a}$ 与向量 $\vec{e}$ 的夹角为 $\frac{2 π}{3}$ ，则向量 $\vec{a}$ 在向量 $\vec{e}$ 方向上的投影向量的坐标为．

查看试题解析
15. 一个三位自然数，百位、十位、个位上的数字依次为a，b，c，当且仅当a＞b，b＜c时称为“凹数”（如213，312等），若a，b，c∈{1，2，3，4}，且a，b，c互不相同，则这个三位数为“凹数”的概率是．

查看试题解析
16. 已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为4，P是 $A A_{1}$ 中点，过点 $D_{1}$ 作平面 $α$ ，满足 $C P ⊥$ 平面 $α$ ，则平面 $α$ 与正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的截面周长为.

查看试题解析

三、解答题

17. 已知 $z_{1} = a + 2 i$ ， $z_{2} = 3 - 4 i$ （其中 $i$ 为虚数单位）.

(1)、若 $\frac{z_{1}}{z_{2}}$ 为纯虚数，求实数 $a$ 的值；

(2)、若 $| z_{1} - \bar{z_{2}} | < | z_{1} |$ （其中 $\bar{z_{2}}$ 是复数 $z_{2}$ 的共轭复数），求实数 $a$ 的取值范围.

查看试题解析
18. 某校命制了一套调查问卷（试卷满分均为100分），并对整个学校的学生进行了测试，先从这些学生的成绩中随机抽取了50名学生的成绩，按照 $[50 ， 60) ， [60 ， 70) ， . . . ， [90 ， 100]$ 分成5组，制成了如图所示的频率分布直方图（假定每名学生的成绩均不低于50分）

(1)、求频率分布直方图中的 $x$ 的值，并估计50名学生的成绩的平均数、中位数（同一组中的数据用该组区间的中点值代表）

(2)、用样本估计总体，若该校共有2000名学生，试估计该校这次成绩不低于70分的人数.

查看试题解析
19. 如图，在平面直角坐标系xOy中， $| \vec{O A} | = 2 ， | \vec{A B} | = 1 ， ∠ O A B = \frac{2 π}{3} ， \vec{B C} = (- 1 ， \sqrt{3})$ ．

(1)、求点B，点C的坐标；

(2)、求四边形OABC的面积．

查看试题解析
20. 如图所示，在四棱锥P－ABCD中，底面ABCD为平行四边形，△PCD为等边三角形，平面PAC⊥平面PCD，PA⊥CD.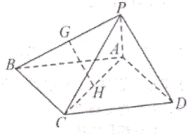

(1)、设G，H分别为PB，AC的中点，求证：GH//平面PAD；

(2)、求证：PA⊥平面PCD．

查看试题解析
21. 进行垃圾分类收集可以减少垃圾处理量和处理设备，降低处理成本，减少土地资源的消耗，具有社会､经济､生态等多方面的效益，是关乎生态文明建设全局的大事.为了普及垃圾分类知识，某学校举行了垃圾分类知识考试，试卷中只有两道题目，已知甲同学答对每题的概率都为 $p$ ，乙同学答对每题的概率都为 $q (p > q)$ ，且在考试中每人各题答题结果互不影响.已知每题甲，乙同时答对的概率为 $\frac{1}{2}$ ，恰有一人答对的概率为 $\frac{5}{12}$ .

(1)、求 $p$ 和 $q$ 的值；

(2)、试求两人共答对3道题的概率.

查看试题解析
22. 如图，矩形 $A B C D$ 是一个历史文物展览厅的俯视图，点 $E$ 在 $A B$ 上，在梯形 $B C D E$ 区域内部展示文物， $D E$ 是玻璃幕墙，游客只能在 $Δ A D E$ 区域内参观．在 $A E$ 上点 $P$ 处安装一可旋转的监控摄像头． $∠ M P N$ 为监控角，其中 $M$ 、 $N$ 在线段 $D E$ （含端点）上，且点 $M$ 在点 $N$ 的右下方．经测量得知： $A D = 6$ 米， $A E = 6$ 米， $A P = 2$ 米， $∠ M P N = \frac{π}{4}$ ．记 $∠ E P M = θ$ (弧度)，监控摄像头的可视区域 $Δ P M N$ 的面积为 $S$ 平方米．

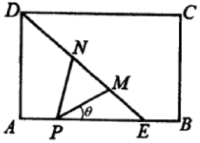(1)、求 $S$ 关于 $θ$ 的函数关系式，并写出 $θ$ 的取值范围；（参考数据： $t a n \frac{5}{4} \approx 3$ ）

(2)、求 $S$ 的最小值．

查看试题解析