2022年江苏省扬州市中考数学模拟卷1
试卷更新日期:2022-04-27 类型:中考模拟
一、选择题(每题3分,共24分)
-
1. ﹣2022的倒数是( )A、 B、 C、﹣2022 D、20222. 如图,是一个小正方体的展开图,把展开图折叠成小正方体后,有“三”字一面的相对面上的字是( )
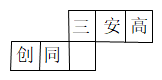 A、高 B、同 C、创 D、安3. 下列事件中,属于必然事件的是( )A、打开电视正在播广告 B、射击运动员只射击1次,恰好命中靶心 C、一组数据的方差越小,则这组数据的波动越小 D、任意购买一张电影票,座位号是3的倍数4. 若分式 的值为0,则x的值为( )A、2 B、-2 C、±2 D、45. 如图,与 , , 分别交于点E,G,F,且 , , 则下列结论不正确的是( )
A、高 B、同 C、创 D、安3. 下列事件中,属于必然事件的是( )A、打开电视正在播广告 B、射击运动员只射击1次,恰好命中靶心 C、一组数据的方差越小,则这组数据的波动越小 D、任意购买一张电影票,座位号是3的倍数4. 若分式 的值为0,则x的值为( )A、2 B、-2 C、±2 D、45. 如图,与 , , 分别交于点E,G,F,且 , , 则下列结论不正确的是( )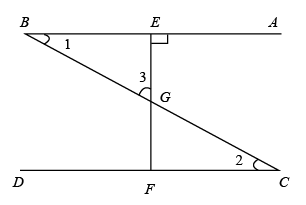 A、 B、 C、 D、6. 如图,△ABC中,AB=AC= ,∠BAC=α°, ,G为BC中点,D为平面内一个动点,且 .将线段BD绕点D逆时针旋转α°,得到DB′,则四边形BACB′面积的最大值为( )
A、 B、 C、 D、6. 如图,△ABC中,AB=AC= ,∠BAC=α°, ,G为BC中点,D为平面内一个动点,且 .将线段BD绕点D逆时针旋转α°,得到DB′,则四边形BACB′面积的最大值为( )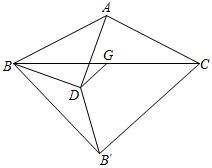 A、24 B、25 C、12 D、137. 如图,正方形ABCD的边长为4,E是BC上一点,过点E作EF⊥AE,交DC于点F,连接AF,则AF的最小值是( )
A、24 B、25 C、12 D、137. 如图,正方形ABCD的边长为4,E是BC上一点,过点E作EF⊥AE,交DC于点F,连接AF,则AF的最小值是( )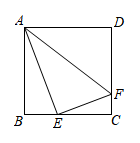 A、5 B、 C、 D、38. 如图,正方形ABCD的边长是 , 以正方形对角线的一半OA为边作正六边形,其中一边与正方形的边CD交于点E,再以点O为圆心OE为半径画弧交AD于点F,则图中阴影部分的的面积为( )
A、5 B、 C、 D、38. 如图,正方形ABCD的边长是 , 以正方形对角线的一半OA为边作正六边形,其中一边与正方形的边CD交于点E,再以点O为圆心OE为半径画弧交AD于点F,则图中阴影部分的的面积为( )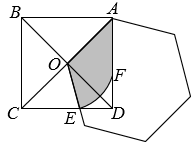 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共30分)
-
9. 某网店2022年母亲节这天的营业额为221000元,将数221000用科学记数法表示为 .10. 若 、 满足 ,则代数式 的值为.11. 不等式组的解集是 .12. 一组数据23,27,20,18,x,12,它们的中位数是21,则x=.13. 扬州雕版印刷技艺历史悠久,元代数学家朱世杰的《算学启蒙》一书曾刻于扬州,该书是中国较早的数学著作之一,书中记载一道问题:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?”题意是:快马每天走240里,慢马每天走150里,慢马先走12天,试问快马几天追上慢马?答:快马天追上慢马.14. 一个“粮仓”的三视图如图所示(单位:m),则它的侧面积是 .
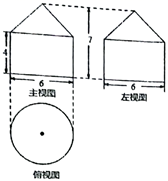 15. 在等边△ABC中,点D在BC边上,BD=3CD,连接AD,以AD为边作等边△ADE,连接CE,若CE=3,则AB的长为 .16. 如图,AB是半圆O的直径,AC=AD,∠CAB=20°,OE⊥CD,OE= , 则半圆O的直径AB是
15. 在等边△ABC中,点D在BC边上,BD=3CD,连接AD,以AD为边作等边△ADE,连接CE,若CE=3,则AB的长为 .16. 如图,AB是半圆O的直径,AC=AD,∠CAB=20°,OE⊥CD,OE= , 则半圆O的直径AB是 17. 如图,在平面直角坐标系中,点 , 点 , I是的内心,则
17. 如图,在平面直角坐标系中,点 , 点 , I是的内心,则 (1)、AB=;(2)、点I关于x轴对称的点的坐标是 .18. 如图①,我们把一个矩形称作一个基本图形,把矩形的顶点及其对称中心称作基本图形的特征点,显然这样的基本图形共有5个特征点,将此基本图形不断地复制并平移,使得相邻两个基本图形的两个特征点重合,这样得到第2个图;第3个图;……;
(1)、AB=;(2)、点I关于x轴对称的点的坐标是 .18. 如图①,我们把一个矩形称作一个基本图形,把矩形的顶点及其对称中心称作基本图形的特征点,显然这样的基本图形共有5个特征点,将此基本图形不断地复制并平移,使得相邻两个基本图形的两个特征点重合,这样得到第2个图;第3个图;……;
 (1)、观察以上图形并完成下表:
(1)、观察以上图形并完成下表:基本图形的个数
1
2
3
4
…
特征点的个数
5
8
11
…
猜想:在第n个图中特征点的个数为(用含n的代数式表示).
(2)、在平面直角坐标系中,点A、点B是坐标轴上的两点,且OA=1,以OA、OB为边作一个矩形,其一条对角线所在直线的解析式为y=x,将此矩形作为基本图形不断复制和平移,如图②所示,若各矩形的对称中心分别为O1、O2、O3、……,则O2022的坐标为 .三、解答题(共10题,共96分)
-
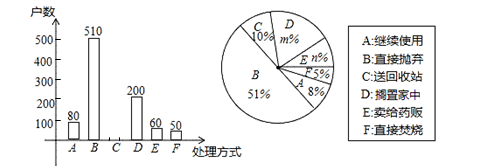
19.(1)、(a+b)(a-2b)-(a-b)2-b(a-b).(2)、20. “通过等价变换,化陌生为熟悉,化未知为已知”是数学学习中解决问题的基本思维方式,例如:解方程 ,就可以利用该思维方式,设 ,将原方程转化为: 这个熟悉的关于y的一元二次方程,解出y,再求x,这种方法又叫“换元法”.请你用这种思维方式和换元法解决下面的问题.已知实数x,y满足 ,求 的值.21. 家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某校学生杨杨和舟舟为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查.
 (1)、下列选取样本的方法最合理的一种是 . (只需填上符合题意答案的序号)
(1)、下列选取样本的方法最合理的一种是 . (只需填上符合题意答案的序号)①在市中心某个居民区以家庭为单位随机抽取;
②在全市医务工作者中以家庭为单位随机抽取;
③在全市常住人口中以家庭为单位随机抽取.
(2)、本次抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如图:①m= ▲ ;n= ▲ ;
②补全条形统计图;
③根据调查数据,你认为该市市民家庭处理过期药品最常见的方式是 ▲ ;
④家庭过期药品的正确处理方式是送回收站点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收站点.
22. 如图,线段AD是△ABC的角平分线.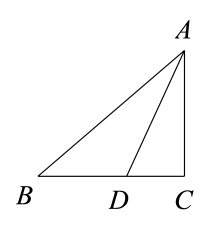 (1)、尺规作图:作线段AD的垂直平分线分别交AB,AC于点E,F:(保留痕迹,不写作法)(2)、在(1)所作的图中,连接DE,DF,求证:四边形AEDF是菱形.23. 为庆祝“三八妇女节”,某地举行歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,甲先从中随机抽取一张卡片,放回后洗匀,再由乙从中随机抽取一张卡片,进行歌咏比赛.(1)、甲抽中歌曲《我和我的祖国》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出甲和乙抽中不同歌曲的概率.24. 为保障新冠病毒疫苗接种需求,某生物科技公司开启“加速”模式,生产效率比原先提高了20%,现在生产240万剂疫苗所用的时间比原先生产220万剂疫苗所用的时间少0.5天,问原先每天生产多少万剂疫苗?25. 如图,点A,C是上的点,且 , 过点A作 , 连接BC交于点D,点D是BC的中点.
(1)、尺规作图:作线段AD的垂直平分线分别交AB,AC于点E,F:(保留痕迹,不写作法)(2)、在(1)所作的图中,连接DE,DF,求证:四边形AEDF是菱形.23. 为庆祝“三八妇女节”,某地举行歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,甲先从中随机抽取一张卡片,放回后洗匀,再由乙从中随机抽取一张卡片,进行歌咏比赛.(1)、甲抽中歌曲《我和我的祖国》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出甲和乙抽中不同歌曲的概率.24. 为保障新冠病毒疫苗接种需求,某生物科技公司开启“加速”模式,生产效率比原先提高了20%,现在生产240万剂疫苗所用的时间比原先生产220万剂疫苗所用的时间少0.5天,问原先每天生产多少万剂疫苗?25. 如图,点A,C是上的点,且 , 过点A作 , 连接BC交于点D,点D是BC的中点.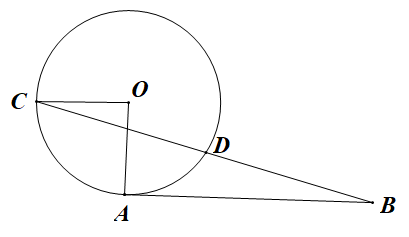 (1)、求的度数;(2)、求的值.26. 已知抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,C为抛物线的顶点,抛物线的对称轴交x轴于点D,连接BC,且tan∠CBD , 如图所示.
(1)、求的度数;(2)、求的值.26. 已知抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,C为抛物线的顶点,抛物线的对称轴交x轴于点D,连接BC,且tan∠CBD , 如图所示.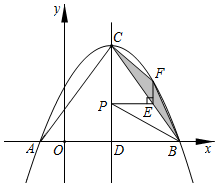 (1)、求抛物线的解析式;(2)、设P是抛物线的对称轴上的一个动点.
(1)、求抛物线的解析式;(2)、设P是抛物线的对称轴上的一个动点.①过点P作x轴的平行线交线段BC于点E,过点E作EF⊥PE交抛物线于点F,连接FB、FC,求△BCF的面积的最大值;
②连接PB,求PC+PB的最小值.
27. 实践与探究情境:在正方形ABCD中,AB=5,点F在AC上,且 , 过点F作EF⊥AC,交CD于点E,连接AE,AF.
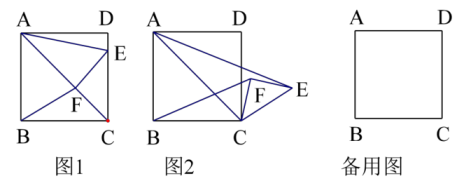 (1)、问题发现
(1)、问题发现图(1)中,线段AE与BF的数量关系是;
直线AE与直线BF的夹角的度数是 .
(2)、问题拓展当△CEF绕点C顺时针旋转时,(1)中的结论是否成立?若成立,请仅就图2的情形给出证明;若不成立,说明理由.
(3)、问题延伸在(2)的条件下,当点F到直线BC的距离为2时,直接写出AE的长.
28. 综合与探究如图,抛物线与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,对称轴与x轴交于点D,点P是直线BC上方抛物线上一点.
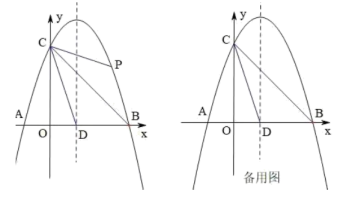 (1)、求抛物线的解析式;(2)、在直线BC上方的抛物线上找一点P,作PG⊥BC,当PG为最大值时,求线段PD的长;(3)、连接CD、CB,当∠PCB=∠DCB时,求点P的坐标.(4)、若点M为直线BC上一点,N为平面内一点,是否存在这样的点M和点N使得以C、D、M、N为顶点的四边形是菱形?若存在,直接写出点M坐标;若不存在,说明理由.
(1)、求抛物线的解析式;(2)、在直线BC上方的抛物线上找一点P,作PG⊥BC,当PG为最大值时,求线段PD的长;(3)、连接CD、CB,当∠PCB=∠DCB时,求点P的坐标.(4)、若点M为直线BC上一点,N为平面内一点,是否存在这样的点M和点N使得以C、D、M、N为顶点的四边形是菱形?若存在,直接写出点M坐标;若不存在,说明理由.