2022年江苏省连云港市中考数学模拟卷1
试卷更新日期:2022-04-27 类型:中考模拟
一、选择题(每题3分,共24分)
-
1. -7的相反数是( )A、-7 B、 C、 D、72. 下列计算正确的是( )A、 B、 C、 D、3. 近年来,国家高度重视精准扶贫,收效显著.据不完全统计6年间全国约有82000000人脱贫.数字82000000用科学记数法表示为( )A、 B、 C、 D、4. 如果一个正多边形的内角和是900°,则这个正多边形是( )A、正七边形 B、正九边形 C、正五边形 D、正十边形5. 将一对直角三角板如图放置,点C在的延长线上,点B在上, , , , , 则( )
 A、 B、 C、 D、6. 如图,在平面直角坐标系中,菱形 的边 在x轴的正半轴上,反比例函数 的图象经过对角线 的中点D和顶点C若菱形 的面积为9,则k的值为( )
A、 B、 C、 D、6. 如图,在平面直角坐标系中,菱形 的边 在x轴的正半轴上,反比例函数 的图象经过对角线 的中点D和顶点C若菱形 的面积为9,则k的值为( ) A、 B、 C、 D、7. 如图, , AC与BD交于点O,过点O作 , 分别交AB,CD于点E,F,则下列结论不正确的是( )
A、 B、 C、 D、7. 如图, , AC与BD交于点O,过点O作 , 分别交AB,CD于点E,F,则下列结论不正确的是( ) A、 B、 C、 D、8. 如图,正方形ABCD的边长是 , 以正方形对角线的一半OA为边作正六边形,其中一边与正方形的边CD交于点E,再以点O为圆心OE为半径画弧交AD于点F,则图中阴影部分的的面积为( )
A、 B、 C、 D、8. 如图,正方形ABCD的边长是 , 以正方形对角线的一半OA为边作正六边形,其中一边与正方形的边CD交于点E,再以点O为圆心OE为半径画弧交AD于点F,则图中阴影部分的的面积为( )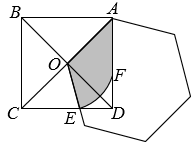 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共24分)
-
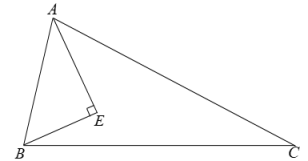
9. 从2022年起长沙市学校体育中考增加素质类选测项目:立定跳远和1分钟跳绳.小熙选择了1分钟跳绳项目,她10次跳绳训练的成绩为140,155,142,155,166,167,166,170,180,176,这组数据的中位数是.10. .11. 分解因式: .12. 已知关于x的方程x2-3x+k=0有两个不相等的实数根,则k的取值范围是13. 已知如图,在ABC中,BAE=CAE,BEAE于点E,若ABC=3ACB,则AB,AC,BE之间的数量关系 .
 14. 如图,线段 , 用尺规作图法按如下步骤作图.
14. 如图,线段 , 用尺规作图法按如下步骤作图.
⑴过点B作的垂线,并在垂线上取;
⑵连接 , 以点C为圆心,为半径画弧,交于点E;
⑶以点A为圆心,为半径画弧,交于点D.即点D为线段的黄金分割点.
则线段的长度约为(结果保留两位小数,参考数据:)
15. 某地的药材批发公司指导农民养植和销售某种药材,经市场调研发现1-8月份这种药材售价(元)与月份之间存在如下表所示的一次函数关系,同时,每千克的成本价(元)与月份之间近似满足如图所示的抛物线,观察两幅图表,试判断 月份出售这种药材获利最大.月份
...
3
6
...
每千克售价
...
8
6
...
 16. 在平面直角坐标系xOy中,已知 , , 三点,其中 , 函数的图象分别与线段BC,AC交于点P,Q.若 , 则t的值为.
16. 在平面直角坐标系xOy中,已知 , , 三点,其中 , 函数的图象分别与线段BC,AC交于点P,Q.若 , 则t的值为.
三、解答题(共11题,共102分)
-
17. 计算:(﹣1)2020﹣﹣(3﹣π)0+|3﹣|+(tan30°)﹣1 .18. 解不等式组:19. 解分式方程:20. 家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某校学生杨杨和舟舟为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查.
 (1)、下列选取样本的方法最合理的一种是 . (只需填上符合题意答案的序号)
(1)、下列选取样本的方法最合理的一种是 . (只需填上符合题意答案的序号)①在市中心某个居民区以家庭为单位随机抽取;
②在全市医务工作者中以家庭为单位随机抽取;
③在全市常住人口中以家庭为单位随机抽取.
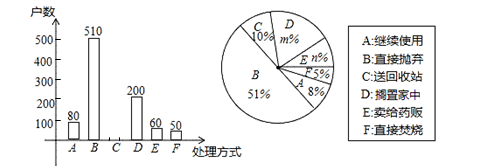
(2)、本次抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如图:①m= ▲ ;n= ▲ ;
②补全条形统计图;
③根据调查数据,你认为该市市民家庭处理过期药品最常见的方式是 ▲ ;
④家庭过期药品的正确处理方式是送回收站点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收站点.
21. 根据省教育厅《关于认真做好2022年初中毕业生升学体育考试工作的通知》精神,凡报考我市普通高中、中等职业学校、五年制高职的应届、往届初中毕业生,均须参加2022年初中毕业升学体育考试,考试项目分为必考项目和选考项目,必考项目含男生1000米跑,女生800米跑;选考项目由考上从七个项目中任选2项,男生选考项目含50米跑、立定跳远、投掷实心球、引体向上、篮球运球、足球运球、排球垫球,女生选考项目含50米跑、立定跳远、一分钟仰卧起坐、引体向上、篮球运球、足球运球、排球垫球.小康决定从50米跑、立定跳远、投掷实心球(分别用A,B,C表示)选2项考试,每个项目选到的可能性相同(1)、“小康选到引体向上”是事件;(2)、请用列表或画树状图的方法,求小康选到50米跑、立定跳远的概率.22. 如图,在四边形ABCD中,∠ACB=90°, , 点E是AB的中点,连接EC,过点E作EF⊥AD,垂足为F,已知 .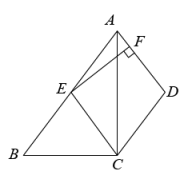 (1)、求证:四边形AECD是菱形:(2)、若AB=25,BC=15,求线段EF的长23. 某公司后勤部准备去超市采购牛奶和咖啡若干箱,现有两种不同的购买方案,如表:
(1)、求证:四边形AECD是菱形:(2)、若AB=25,BC=15,求线段EF的长23. 某公司后勤部准备去超市采购牛奶和咖啡若干箱,现有两种不同的购买方案,如表:牛奶(箱)
咖啡(箱)
金额(元)
方案一
20
10
1100
方案二
10
20
1300
(1)、求牛奶与咖啡每箱分别为多少元;(2)、超市中该款咖啡和牛奶有部分因保质期临近,进行打六折的促销活动,后勤部根据需要选择原价或打折的咖啡和牛奶,此次采购共花费了1800元,其中购买打折的牛奶箱数是所有牛奶、咖啡的总箱数的 , 则此次按原价采购的咖啡有 箱.(直接写出答案)24. 如图,已知ABC内接于⊙O,AB是⊙O的直径,∠CAB的平分线交BC于点D,交⊙O于点E,连接EB,作∠BEF=∠CAE,交AB的延长线于点F.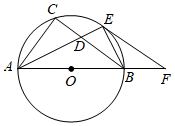 (1)、求证:EF是⊙O的切线;(2)、若BF=10,EF=20,求⊙O的半径和AD的长.25. 如图所示的是一款机械手臂,由上臂、中臂和底座三部分组成,其中上臂和中臂可自由转动,底座与水平地面垂直.在实际运用中要求三部分始终处于同一平面内,其示意图如图1所示,经测量,上臂 , 中臂 , 底座
(1)、求证:EF是⊙O的切线;(2)、若BF=10,EF=20,求⊙O的半径和AD的长.25. 如图所示的是一款机械手臂,由上臂、中臂和底座三部分组成,其中上臂和中臂可自由转动,底座与水平地面垂直.在实际运用中要求三部分始终处于同一平面内,其示意图如图1所示,经测量,上臂 , 中臂 , 底座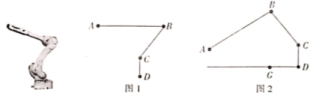 (1)、若上臂与水平面平行, . 计算点到地面的距离.(2)、在一次操作中,中臂与底座成夹角,上臂与中臂夹角为 , 如图2,计算这时点到地面的距离.与图1状态相比,这时点A向前伸长了多少?26. 抛物线交x轴于点A,B(A在B的左边),交y轴于点C,顶点为M,对称轴MD交x轴于点D,E是线段MD上一动点,以OB,BE为邻边作平行四边形OBEF,EF交抛物线于点P,G(P在G的左边),交y轴于点H.
(1)、若上臂与水平面平行, . 计算点到地面的距离.(2)、在一次操作中,中臂与底座成夹角,上臂与中臂夹角为 , 如图2,计算这时点到地面的距离.与图1状态相比,这时点A向前伸长了多少?26. 抛物线交x轴于点A,B(A在B的左边),交y轴于点C,顶点为M,对称轴MD交x轴于点D,E是线段MD上一动点,以OB,BE为邻边作平行四边形OBEF,EF交抛物线于点P,G(P在G的左边),交y轴于点H.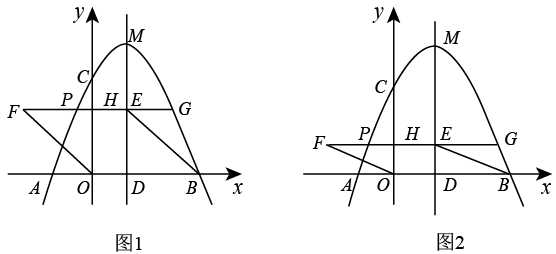 (1)、求点A,B,C的坐标;(2)、如图1,当时,求DE的长;(3)、如图2,当时,
(1)、求点A,B,C的坐标;(2)、如图1,当时,求DE的长;(3)、如图2,当时,①求直线FC的解析式,并判断点M是否落在该直线上.
②连接CG,MG,CP,MP,记的面积为 , 的面积为 , 则 ▲ .
27. 综合与实践问题情境
Rt△ABC和Rt△DEF如图1放置,点B与点D重合,∠ACB=∠EDF=90°,∠A=30°,AB=ED=FD=4,EF分别与AC,AB交于点N,点P,点M是AB的中点.
 (1)、数学思考
(1)、数学思考连接MN,求证:点N是EF的中点;并计算△MNP的面积;
(2)、操作探究如图2,先将△DEF沿BC的方向平移,使点D与点C重合,再沿CA的方向平移到点D为AC的中点时停止;过点C作CH∥AB交DE于点H,连接AH,AN,CM.试判断四边形AMCH的形状,并说明理由;
 (3)、在图2的基础上,将△DEF绕着点D顺时针旋转30°,CH∥AB仍然存在,延长CH交MN于点G,交EF于点Q,如图3.请直接写出三角形CMG的面积.
(3)、在图2的基础上,将△DEF绕着点D顺时针旋转30°,CH∥AB仍然存在,延长CH交MN于点G,交EF于点Q,如图3.请直接写出三角形CMG的面积.