2022年江苏省苏州市中考数学模拟卷1
试卷更新日期:2022-04-27 类型:中考模拟
一、填空题(每题3分,共24分)
-
1. 根据安徽省统计局数据,2021年安徽GDP约为43000亿元,同比增长8.3%,增速比全国(8.1%)快0.2个百分点,居全国第8位.将43000用科学记数法表示为 .2. 因式分解: .3. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的吉祥码示意图,用黑白打印机打印在边长为2cm的正方形区域内,图中黑色部分的总面积为2.4cm2 , 现在向正方形区域内随机掷点,点落入黑色部分的概率为 .
 4. 如图,在ABC中, , 在同一平面内,将ABC绕点A逆时针旋转到的位置,使 , 作交BC于点D,则 .
4. 如图,在ABC中, , 在同一平面内,将ABC绕点A逆时针旋转到的位置,使 , 作交BC于点D,则 .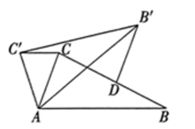 5. 如果m是方程x2+2x-3=0的实根,那么代数式m3-7m的值是 .6. 已知函数y=kx2-2x+1的图象与x轴只有一个交点,则k的值为7. 如图,点O是菱形ABCD对角线的交点,DEAC,CEBD,连接OE,设AC=12,BD=16,则OE的长为 .
5. 如果m是方程x2+2x-3=0的实根,那么代数式m3-7m的值是 .6. 已知函数y=kx2-2x+1的图象与x轴只有一个交点,则k的值为7. 如图,点O是菱形ABCD对角线的交点,DEAC,CEBD,连接OE,设AC=12,BD=16,则OE的长为 . 8. 如图,在中, , , , 将绕点C顺时针旋转得到 , 点B恰好在斜边上,则线段CA扫过的面积为 . 则点A经过的路径的长为 .
8. 如图,在中, , , , 将绕点C顺时针旋转得到 , 点B恰好在斜边上,则线段CA扫过的面积为 . 则点A经过的路径的长为 .
二、解答题(共10题,共76分)
-
9. 计算: .10. 解方程组: .11. 先化简,再求值: ,其中 .12. 为落实重庆市关于开展中小学课后服务工作的要求,某学校开展了四门校本课程供学生选择:A.趣味数学;B.博乐阅读;C.快乐英语;D.硬笔书法.全校共有100名学生选择了A课程,为了解选A课程学生的学习情况,从这100名学生中随机抽取了30名学生进行测试.将他们的成绩(百分制)绘制成频数分布直方图.
 (1)、其中70≤x<80这一组的数据为74,73,72,75,76,76,79,则这组数据的中位数是 ,众数是(2)、根据题中信息,估计该校共有 人,选A课程学生成绩在80≤x<90的有 人.(3)、课程D在扇形统计图中所对应的圆心角的度数为(4)、如果学校规定每名学生要选两门不同的课程,小张和小王在选课程中,若第一次都选了课程C,那么他俩第二次同时选课程A或B的概率是多少?请用列表法或画树状图的方法加以说明.13. 为庆祝“三八妇女节”,某地举行歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,甲先从中随机抽取一张卡片,放回后洗匀,再由乙从中随机抽取一张卡片,进行歌咏比赛.(1)、甲抽中歌曲《我和我的祖国》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出甲和乙抽中不同歌曲的概率.14. 如图,一次函数y=kx+b的图象与反比例函数y= 的图象在第一象限内交于点A , 与x轴交于点B(5,0),若OB=AB , 且S△OAB= ,求反比例函数与一次函数的表达式.
(1)、其中70≤x<80这一组的数据为74,73,72,75,76,76,79,则这组数据的中位数是 ,众数是(2)、根据题中信息,估计该校共有 人,选A课程学生成绩在80≤x<90的有 人.(3)、课程D在扇形统计图中所对应的圆心角的度数为(4)、如果学校规定每名学生要选两门不同的课程,小张和小王在选课程中,若第一次都选了课程C,那么他俩第二次同时选课程A或B的概率是多少?请用列表法或画树状图的方法加以说明.13. 为庆祝“三八妇女节”,某地举行歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,甲先从中随机抽取一张卡片,放回后洗匀,再由乙从中随机抽取一张卡片,进行歌咏比赛.(1)、甲抽中歌曲《我和我的祖国》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出甲和乙抽中不同歌曲的概率.14. 如图,一次函数y=kx+b的图象与反比例函数y= 的图象在第一象限内交于点A , 与x轴交于点B(5,0),若OB=AB , 且S△OAB= ,求反比例函数与一次函数的表达式.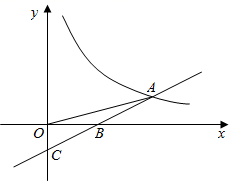 15. 如图,为⊙O的直径,过点的切线与弦的延长线交于点 , 为半径,于点 , 连接 .
15. 如图,为⊙O的直径,过点的切线与弦的延长线交于点 , 为半径,于点 , 连接 . (1)、求证:;(2)、若 , 求的长.16. 已知:抛物线y=-x2+kx+k+1(k>1)与x轴交于A、B两点,(点A在点B的左侧),与y轴交于点C.(1)、k=2时,求抛物线的顶点坐标;(2)、若抛物线经过一个定点,求这个定点的坐标;(3)、点P为抛物线上一点,且位于直线BC上方,过点P作PF∥y轴,交BC于点F,求PF长度的最大值(用含k式子表示).17. 某企业接到一批帽子生产任务,按要求在20天内完成,约定这批帽子的出厂价为每顶8元.为按时完成任务,该企业招收了新工人,设新工人小华第x天生产的帽子数量为y顶,y与x满足如下关系式:y=
(1)、求证:;(2)、若 , 求的长.16. 已知:抛物线y=-x2+kx+k+1(k>1)与x轴交于A、B两点,(点A在点B的左侧),与y轴交于点C.(1)、k=2时,求抛物线的顶点坐标;(2)、若抛物线经过一个定点,求这个定点的坐标;(3)、点P为抛物线上一点,且位于直线BC上方,过点P作PF∥y轴,交BC于点F,求PF长度的最大值(用含k式子表示).17. 某企业接到一批帽子生产任务,按要求在20天内完成,约定这批帽子的出厂价为每顶8元.为按时完成任务,该企业招收了新工人,设新工人小华第x天生产的帽子数量为y顶,y与x满足如下关系式:y= (1)、小华第几天生产的帽子数量为220顶?(2)、如图,设第x天每顶帽子的成本是z元,z与x之间的关系可用图中的函数图象来刻画.若小华第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大值是多少元?(3)、设(2)小题中第m天利润达到最大值,若要使第(m+1)天的利润比第m天的利润至少多49元,则第(m+1)天每顶帽子至少应提价几元?18. 在中, , , 点P在AB边上, , 将线段AP绕点P顺时针旋转至PD,记旋转角为 , 连接BD,以BD为底边,在线段BD的上方找一点E,使 , ED=EB,连接AD、CE.
(1)、小华第几天生产的帽子数量为220顶?(2)、如图,设第x天每顶帽子的成本是z元,z与x之间的关系可用图中的函数图象来刻画.若小华第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大值是多少元?(3)、设(2)小题中第m天利润达到最大值,若要使第(m+1)天的利润比第m天的利润至少多49元,则第(m+1)天每顶帽子至少应提价几元?18. 在中, , , 点P在AB边上, , 将线段AP绕点P顺时针旋转至PD,记旋转角为 , 连接BD,以BD为底边,在线段BD的上方找一点E,使 , ED=EB,连接AD、CE. (1)、如图1,当旋转角时,请直接写出线段CE与线段AD的数量关系;(2)、当时,
(1)、如图1,当旋转角时,请直接写出线段CE与线段AD的数量关系;(2)、当时,①如图2,(1)中线段CE与线段AD的数量关系是否还成立?并说明理由.
②如图3,当点A、D、E三点共线时,连接CD,判断四边形CDBE的形状,并说明理由.
三、选择题(每题3分,共30分)
-
19. 化简 的结果是( )A、-4 B、4 C、±4 D、220. 如图所示是一个放在水平面上的几何体,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 21. 如图,将△AOB绕着点O顺时针旋转,得到△COD,若∠AOB=40°,∠BOC=30°,则旋转角度是( )
21. 如图,将△AOB绕着点O顺时针旋转,得到△COD,若∠AOB=40°,∠BOC=30°,则旋转角度是( ) A、10° B、30° C、40° D、70°22. 下列运算正确的是( )A、 B、 C、 D、23. 一组样本数据为1、2、3、3、6,下列说法不正确的是( )A、平均数是3 B、中位数是3 C、方差是3 D、众数是324. 下列函数中,y随x的增大而减小的是( )A、y=x+1 B、y=2x2(x>0) C、y=﹣x2(x<0) D、y=﹣x2(x>0)25. 《九章算术》是中国古代数学著作之一,书中有这样的一个问题:今有甲、乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?题意为:今有甲、乙二人,不知其钱包里有多少钱.若乙把其一半的钱给甲,则甲的钱数为50;而甲把其的钱给乙,则乙的钱数也能为50,问甲、乙各有多少钱?解:设甲原有钱数为x,乙原有钱数为y,依题意可得方程组为( )A、 B、 C、 D、26. 将二次函数的图象平移后,得到二次函数的图象,平移的方法可以是( )A、向左平移1个单位长度 B、向右平移1个单位长度 C、向上平移1个单位长度 D、向下平移1个单位长度
A、10° B、30° C、40° D、70°22. 下列运算正确的是( )A、 B、 C、 D、23. 一组样本数据为1、2、3、3、6,下列说法不正确的是( )A、平均数是3 B、中位数是3 C、方差是3 D、众数是324. 下列函数中,y随x的增大而减小的是( )A、y=x+1 B、y=2x2(x>0) C、y=﹣x2(x<0) D、y=﹣x2(x>0)25. 《九章算术》是中国古代数学著作之一,书中有这样的一个问题:今有甲、乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?题意为:今有甲、乙二人,不知其钱包里有多少钱.若乙把其一半的钱给甲,则甲的钱数为50;而甲把其的钱给乙,则乙的钱数也能为50,问甲、乙各有多少钱?解:设甲原有钱数为x,乙原有钱数为y,依题意可得方程组为( )A、 B、 C、 D、26. 将二次函数的图象平移后,得到二次函数的图象,平移的方法可以是( )A、向左平移1个单位长度 B、向右平移1个单位长度 C、向上平移1个单位长度 D、向下平移1个单位长度

