广西百色市2021-2022学年高一下学期数学期中模拟试卷
试卷更新日期:2022-04-26 类型:期中考试
一、单选题
-
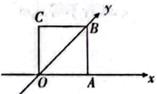
1. 在复平面内,复数对应的点坐标为( )A、 B、 C、 D、2. 在△ABC中,若 , , , 则角B的大小为( )A、 B、 C、 D、或3. 已知向量 , 且 , 则实数a的值为( )A、1 B、 C、或-1 D、或14. 若△ABC外接圆圆心为 ,半径为4,且 则 的值为( )A、14 B、 C、 D、25. 一个斜边长为的等腰直角三角形绕直角边旋转一周形成的几何体的体积为( )A、 B、 C、 D、π6. 如图,正方形 的边长为1,它是水平放置的一个平面图形的直观图,则原图形的面积为( )
 A、 B、1 C、 D、7. 在棱长为1的正方体中,点为棱的中点,则点到平面的距离为( )
A、 B、1 C、 D、7. 在棱长为1的正方体中,点为棱的中点,则点到平面的距离为( )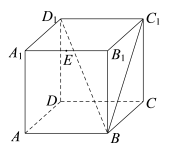 A、 B、 C、 D、8. 《九章算术》是我国古代内容极其丰富的数学名著,书中有如下问题:“今有委菽依组内角,下周三丈,高七尺,问积及为菽几何?”其意思为:“靠墙壁堆放大豆成半圆锥形,大豆堆底面的弧长为3丈,高为7尺,问大豆堆体积和堆放的大豆有多少斛?”已知1斛大豆=243立方尺,1丈=10尺,圆周率约为3,估算出堆放的大豆有( )A、140斛 B、142斛 C、144斛 D、146斛
A、 B、 C、 D、8. 《九章算术》是我国古代内容极其丰富的数学名著,书中有如下问题:“今有委菽依组内角,下周三丈,高七尺,问积及为菽几何?”其意思为:“靠墙壁堆放大豆成半圆锥形,大豆堆底面的弧长为3丈,高为7尺,问大豆堆体积和堆放的大豆有多少斛?”已知1斛大豆=243立方尺,1丈=10尺,圆周率约为3,估算出堆放的大豆有( )A、140斛 B、142斛 C、144斛 D、146斛二、多选题
-
9. 在空间中,已知a,b,c是三条不同的直线,是一平面,下列说法正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , 则10. 一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径相等,下列结论正确的是( )A、圆柱的侧面积为 B、圆锥的侧面积为 C、圆柱的侧面积与球的表面积相等 D、球的体积是圆锥体积的两倍11. 下列式子中,一定正确的是( )A、 B、 C、 D、12. 下列命题正确的是( )A、 B、相反向量 , ,满足 C、向量 , 能作为所在平面内的一组基底 D、对于向量 , ,有 不一定成立
三、填空题
-
13. 已知向量 , , 若 , 则.14. 已知锐角的面积为9, , 点D在边上,且 , 则的长为 .15. 设 , 复数 , , 若是纯虚数,则 .16. 如图,在边长为2的正方体中,点P是该正方体对角线上的动点,给出下列四个结论:
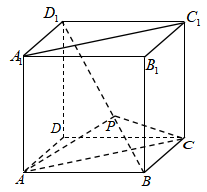
①
②面积的最大值是
③面积的最小值是
④当时,平面平面
其中所有正确结论的序号是.
四、解答题
-
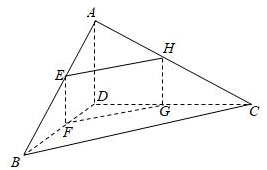
17. 西昌市邛泸旅游风景区在邛海举行搜救演练,如图, , 是邛海水面上位于东西方向相距 公里的两个观测点,现位于 点北偏东 、 点西北方向的 点有一艘渔船发出求救信号,位于 点南偏西 且与 点相距 公里的 点的救援船立即前往营救,其航行速度为30公里/小时。

求:
(1)、观测点 与 点处的渔船间的距离。(2)、 点的救援船到达 点需要多长时间?18. 已知(1)、求;(2)、设的夹角为θ,求cosθ的值;(3)、若向量与互相垂直,求k的值.19. 如图所示长方体 中, , 是 的中点.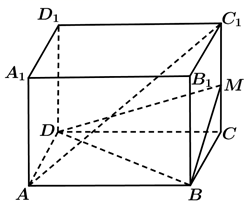 (1)、证明: 平面 ;(2)、若 是 的中点,求三棱锥 的体积.20. 在△ABC中,角所对的边分别为 , 已知.(1)、求的大小;(2)、的面积等于 , D为BC边的中点,当中线AD长最短时,求AB边长.
(1)、证明: 平面 ;(2)、若 是 的中点,求三棱锥 的体积.20. 在△ABC中,角所对的边分别为 , 已知.(1)、求的大小;(2)、的面积等于 , D为BC边的中点,当中线AD长最短时,求AB边长.