安徽省合肥市庐江县柯坦乐桥片区2022年中考数学第一次模拟试卷
试卷更新日期:2022-04-26 类型:中考模拟
一、单选题
-
1. - 的相反数是( )A、 B、-2 C、- D、22. 2021年5月15日7时18分,天问一号探测器成功着陆火星,中国首次火星探测任务取得成功.“祝融号”火星车在距离地球约3.2亿千米的火星上进行巡视探测,3.2亿千米用科学记数法可表示为( )A、0.32×10千米 B、3.2×10千米 C、0.32×10千米 D、3.2×10千米3. 如图所示,该几何体的俯视图是( )
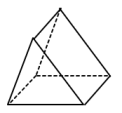 A、
A、 B、
B、 C、
C、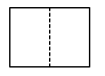 D、
D、 4. 一组数据2、3、5、x、7、4、6、9的唯一众数是5,则这组数据的中位数是( )A、4 B、4.5 C、5 D、5.55. 一个布袋里装有3个只有颜色不同的球,其中2个红球,1个白球.从布袋里摸出一个球,记下颜色后放回,搅匀,再摸出一个球,则两次摸到的球都是红球的概率是( )A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、 D、7. 如图,正五边形的两条对角线相交形成 , 则的度数为( )
4. 一组数据2、3、5、x、7、4、6、9的唯一众数是5,则这组数据的中位数是( )A、4 B、4.5 C、5 D、5.55. 一个布袋里装有3个只有颜色不同的球,其中2个红球,1个白球.从布袋里摸出一个球,记下颜色后放回,搅匀,再摸出一个球,则两次摸到的球都是红球的概率是( )A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、 D、7. 如图,正五边形的两条对角线相交形成 , 则的度数为( ) A、60° B、64° C、72° D、75°8. 黄金分割数 是一个很奇妙的数,大量应用于艺术、建筑和统计决策等方面,请你估算 ﹣1的值( )A、在1.1和1.2之间 B、在1.2和1.3之间 C、在1.3和1.4之间 D、在1.4和1.5之间9. 如图,在中, , CD是斜边AB上的中线,若 , , 则BC的长为( )
A、60° B、64° C、72° D、75°8. 黄金分割数 是一个很奇妙的数,大量应用于艺术、建筑和统计决策等方面,请你估算 ﹣1的值( )A、在1.1和1.2之间 B、在1.2和1.3之间 C、在1.3和1.4之间 D、在1.4和1.5之间9. 如图,在中, , CD是斜边AB上的中线,若 , , 则BC的长为( ) A、2.5 B、3 C、3.5 D、10. 如图,过x轴正半轴上的任意一点P作y轴的平行线,分别与反比例函数 , 的图象交于A,B两点,若C是y轴上任意一点,连接AC、BC,则的面积为( )
A、2.5 B、3 C、3.5 D、10. 如图,过x轴正半轴上的任意一点P作y轴的平行线,分别与反比例函数 , 的图象交于A,B两点,若C是y轴上任意一点,连接AC、BC,则的面积为( ) A、10 B、 C、5 D、
A、10 B、 C、5 D、二、填空题
-
11. 分解因式: .12. 如图,已知⊙O上有三点A、B、C,半径OC=2,∠ABC=30°,切线AP交OC延长线于点P,则△OAP的周长为
 13. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“美学”,如图, , 这个比值介于整数和之间,则的值是 .
13. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“美学”,如图, , 这个比值介于整数和之间,则的值是 . 14. “两直线平行,内错角相等”的逆命题是 .
14. “两直线平行,内错角相等”的逆命题是 .三、解答题
-
15. 解不等式组: .16. 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).

( 1 )将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(1,﹣4),画出平移后对应的△A2B2C2;
( 2 )若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;
( 3 )在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
17. 我国海域辽阔,渔业资源丰富,如图,现有渔船以18km/h的速度在海面上沿正东方向航行,当行至A处时,发现它的东南方向有一灯塔B,船续向东航行30min后达到C处,发现灯塔B在它的南偏东15°方向,求此时渔船与灯塔B的距离. 18. 为了丰富学生社会实践活动,学校组织学生到红色文化基地和人工智能科技馆参观学习.如图,学校在点处,位于学校的东北方向,位于学校南偏东方向,在的南偏西方向的处.求学校和红色文化基地之间的距离.
18. 为了丰富学生社会实践活动,学校组织学生到红色文化基地和人工智能科技馆参观学习.如图,学校在点处,位于学校的东北方向,位于学校南偏东方向,在的南偏西方向的处.求学校和红色文化基地之间的距离. 19. 如图是一种机器零件的左视大致图形,已测得 , , , , , , 求点E到直线CD之间距离EF的长.(结果精确到0.1,参考数据: , , , )
19. 如图是一种机器零件的左视大致图形,已测得 , , , , , , 求点E到直线CD之间距离EF的长.(结果精确到0.1,参考数据: , , , )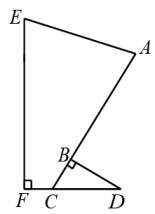 20. 如图,四边形ABCD内接于⊙O, BD为直径,AC平分∠BCD,
20. 如图,四边形ABCD内接于⊙O, BD为直径,AC平分∠BCD,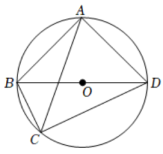 (1)、若BC=5cm,CD=12cm,求AB的长;(2)、求证:BC+CD=AC.21. 邮票素有“国家名片”之称,方寸之间,包罗万象.为宣传2022年北京冬奥会,中国邮政发行了一套冬奥会邮票,其中有一组展现雪上运动的邮票,如图所示:
(1)、若BC=5cm,CD=12cm,求AB的长;(2)、求证:BC+CD=AC.21. 邮票素有“国家名片”之称,方寸之间,包罗万象.为宣传2022年北京冬奥会,中国邮政发行了一套冬奥会邮票,其中有一组展现雪上运动的邮票,如图所示:
某班级举行冬奥会有奖问答活动,答对的同学可以随机抽取邮票作为奖品.
(1)、在抢答环节中,若答对一题,可从4枚邮票中任意抽取1枚作为奖品,则恰好抽到“冬季两项”的概率是;(2)、在抢答环节中,若答对两题,则可从4枚邮票中任意抽取2枚作为奖品,求恰好抽到“高山滑雪”和“自由式滑雪”的概率.22. 已知抛物线经过点 , 顶点为B.(1)、求a的值及顶点B的坐标;(2)、求直线AB的函数表达式;(3)、若P是抛物线上一动点,设点P的横坐标为 , 的面积为S,求S的最大值.23. 数学模型学习与应用.【学习】如图1, , , 于点C,于点E.由 , 得∠1=∠D;又 , 可以通过推理得到≌ . 我们把这个数学模型称为“一线三等角”模型; (1)、【应用】如图2,点B,P,D都在直线l上,并且 . 若 , , , 用含x的式子表示CD的长;(2)、【拓展】在中,点D,E分别是边BC,AC上的点,连接AD,DE, , , . 若为直角三角形,求CD的长;(3)、如图3,在平面直角坐标系xOy中,点A的坐标为 , 点B为平面内任一点.是以OA为斜边的等腰直角三角形,试直接写出点B的坐标.
(1)、【应用】如图2,点B,P,D都在直线l上,并且 . 若 , , , 用含x的式子表示CD的长;(2)、【拓展】在中,点D,E分别是边BC,AC上的点,连接AD,DE, , , . 若为直角三角形,求CD的长;(3)、如图3,在平面直角坐标系xOy中,点A的坐标为 , 点B为平面内任一点.是以OA为斜边的等腰直角三角形,试直接写出点B的坐标.