广东省佛山市三水区2022年中考模拟数学试题

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. -7的相反数是（　　）

A、 $- 7$ B、 $7$ C、 $- \frac{1}{7}$ D、 $\frac{1}{7}$

查看试题解析
2. 长征二号F遥十三运载火箭在酒泉卫星发射中心将神舟十三号送入近地点高度200000m，远地点高度356000m的近地轨道．其中数字356000用科学记数法表示为（）

A、35.6×10⁴ B、3.56×10⁵ C、3.56×10⁶ D、0.356×10⁶

查看试题解析
3. 如图所示的几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 2022年冬奥会古祥物为“冰墩墩”，冬残奥会吉祥物为“雪容融”.如图，现有三张正面印有吉祥物的不透明卡片，卡片除正面图案不同外，其余均相同，其中两张正面印有冰墩墩图案，一张正面印有雪容融图案，将三张卡片正面向下洗匀，从中随机抽取两张卡片，则抽出的两张都是冰墩墩卡片的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{4}{9}$ D、 $\frac{2}{3}$

查看试题解析
5. 下列运算中，正确的是（）

A、（﹣a）⁶÷（﹣a）³＝﹣a³ B、（﹣3a³）²＝6a⁶ C、（ab²）³＝ab⁶ D、a³•a²＝a⁶

查看试题解析
6. 关于x的一元二次方程x²+px﹣2＝0的一个解为 $x_{1} ＝ 2$ ，则另一个解x₂为（）

A、1 B、﹣1 C、﹣2 D、2

查看试题解析
7. 如图，C，D在⊙O上，AB是直径，∠D＝64°，则∠BAC＝（）

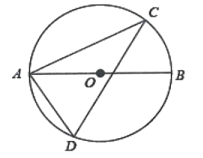A、64° B、34° C、26° D、24°

查看试题解析
8. 在平面直角坐标系中，将一次函数 $y = 2 x + 4$ 的图象沿x轴向右平移 $m (m > 0)$ 个单位后，经过点 $(1 ， - 2)$ ，则m的值为（）

A、4 B、6 C、8 D、10

查看试题解析
9. 如图，AC＝BC＝BE＝DE＝10cm，点A、B、D在同一条直线上，AB＝12cm，BD＝16cm，则点C和点E之间的距离是（）

A、6cm B、7cm C、8cm D、 $10 \sqrt{2} c m$

查看试题解析
10. 已知二次函数y＝a(x+1)(x﹣m)（a≠0，1＜m＜2），当x＜﹣1时，y随x的增大而增大，则下列结论正确的是（）
①当x＞2时，y随x的增大而减小；
②若图象经过点(0，1)，则﹣1＜a＜0；
③若(﹣2022，y₁)，(2022，y₂)是函数图象上的两点，则yl＜y₂；
④若图象上两点 $(\frac{1}{4} ， y_{1})$ ， $(\frac{1}{4} + n ， y_{2})$ 对一切正数n，总有y₁＞y₂ ，则1＜m $\leq \frac{3}{2}$ ．

A、①② B、①③ C、①②③ D、①③④

查看试题解析

二、填空题

11. 若 $\frac{x}{y} = \frac{2}{3}$ ，则 $\frac{x + y}{y}$ 的值为．

查看试题解析
12. 关于x的一元二次方程 $x^{2} - x + m = 0$ 有两个不相等的实数根，写出一个满足条件的实数m的值．（写出一个即可）

查看试题解析
13. 如图，平行四边形ABCD的对角线AC，BD相交于点O，点E、F分别是线段AO，BO的中点，若AC+BD＝12cm，△OAB的周长是10cm，则EF＝cm．

查看试题解析
14. 已知点 $P (m - n ， 1)$ 与点 $Q (3 ， m + n)$ 关于原点对称，则 $m =$ ．

查看试题解析
15. 如图，将 $Δ A B C$ 绕点A旋转60度得到 $Δ A D E$ ． $∠ E$ $= 6 5^{°}$ ，且 $A D ⊥ B C$ ，则 $∠ B A C =$

查看试题解析
16. 实践操作：现有两个正方形A，B．如图所示进行两种方式摆放：
方式1：将B放在A的内部，得甲图；
方式2：将A，B并列放置，构造新正方形得乙图．
问题解决：对于上述操作，若甲图和乙图阴影部分的面积分别为1和12，则正方形A，B的面积之和为．

查看试题解析
17. 如图，四边形 $A B C D$ 的顶点坐标分别为 $A (- 4 ， 0)$ ， $B (- 2 ， - 1)$ ， $C (3 ， 0)$ ， $D (0 ， 3)$ ，当过点B的直线l将四边形 $A B C D$ 的面积分成面积相等的两部分时，则直线l的函数表达式为．

查看试题解析

三、解答题

18. 计算： $| - 1 | - \frac{1}{2} \sqrt{8} + 6 c o s 30 ° - {(π - 2021)}^{0}$ .

查看试题解析
19. 根据“五项管理”文件精神，某学校优化学校作业管理，探索减负增效新举措，学校就学生做作业时间进行问卷调查，将收集信息进行统计分成A、B、C、D四个层级，其中A：90分钟以上；B：60～90分钟；C：30～60分钟；D：30分钟以下．并将结果绘制成两幅不完整的统计图，请你根据统计信息解答下列问题：

(1)、接受问卷调查的学生共有人；

(2)、求扇形统计图中“D”等级的扇形的圆心角的度数，并补全条形统计图．

查看试题解析
20. 如图，在平面直角坐标系中，四边形OABC为矩形，点D为AB的中点．一次函数y＝﹣3x+6的图象经过点C、D，反比例函数y＝ $\frac{k}{x}$ （x＞0），求k的值．

查看试题解析
21. 为有效落实双减工作，切实做到减负提质，很多学校决定在课后看护中增加乒乓球项目．体育用品商店得知后，第一次用600元购进乒乓球若干盒，第二次又用600元购进该款乒乓球，但这次每盒的进价是第一次进价的 $\frac{5}{4}$ 倍，购进数量比第一次少了30盒．

(1)、求第一次每盒乒乓球的进价是多少元？

(2)、若要求这两次购进的乒乓球按同一价格全部销售完后获利不低于420元，则每盒乒乓球的售价至少是多少元？

查看试题解析
22. 如图，已知Rt△ABC中，∠BAC＝90°，BC＝6，AC＝4 $\sqrt{2}$ ，以A为圆心，AB为半径画圆，与边BC交于另一点D．

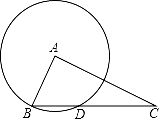(1)、求BD的长；

(2)、连接AD，求∠DAC的余弦值．

查看试题解析
23. 如图，在 $△$ ABC中，BC＝2AB，AD是BC边上的中线，O是AD的中点，过点A作AE $∥$ BC，交BO的延长线于点E，BE交AC于点F，连接DE交AC于点G．

(1)、判断四边形ABDE的形状，并说明理由；

(2)、若 $A B = \sqrt{34}$ ，且OA：OB＝3：5，求四边形ABDE的面积；

(3)、连接DF，求证：DF²＝FG•FC．

查看试题解析
24. 已知抛物线y＝a（x﹣2）²（a≠0）交y轴于点B(0，2)，顶点为点A，且与直线l交于不同的两点M、N（M、N不与点A重合），点D(2，2)在直线l上．

(1)、求抛物线的解析式；

(2)、若点N的坐标为(6n，n)，且点N在抛物线对称轴的右侧，请证明∠MAN＝90°；

(3)、过点A作AE⊥l，垂足为点E，求点B到点E的最短距离．

查看试题解析