广东省广州市花都区2022年中考数学模拟试题

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 绝对值小于3的整数有（　　）

A、2个 B、3个 C、5个 D、6个

查看试题解析
2. 下列交通标志，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 一组数据﹣3，3，﹣2，3，1的中位数是（　　）

A、﹣3 B、﹣2 C、1 D、3

查看试题解析
4. 下列计算中正确的是（　　）

A、a²+a³＝a⁵ B、4a⁴÷a＝3a⁴ C、a²•a⁴＝a⁸ D、（a²）³＝a⁶

查看试题解析
5. A，B两个点的坐标分别为（3，4），（﹣5，1），以原点O为圆心，5为半径作⊙O，则下列说法正确的是（　　）

A、点A，点B都在⊙O上 B、点A在⊙O上，点B在⊙O外 C、点A在⊙O内，点B在⊙O上 D、点A，点B都在⊙O外

查看试题解析
6. 如图， $A B$ 是河堤横断面的迎水坡，堤高 $A C = \sqrt{3}$ ，水平距离 $B C = 1$ ，则斜坡 $A B$ 的坡度为（）

A、 $\sqrt{3}$ B、 $\frac{\sqrt{3}}{3}$ C、 $30^{\circ}$ D、 $60^{\circ}$

查看试题解析
7. 如图，在 $Δ A B C$ 中， $∠ A C B = 90^{°} ， D$ 是 $A B$ 的中点，则下列结论不一定正确的是（）

A、 $C D = B D$ B、 $∠ A = ∠ D C A$ C、 $B D = A C$ D、 $∠ B + ∠ A C D = 90^{°}$

查看试题解析
8. 抛物线y＝﹣x²+2x+m+1（m为常数）交y轴于点A，与x轴的一个交点在2和3之间，顶点为B．有下列结论：①关于x的方程﹣x²+2x+m+1（m为常数）＝0有两个不相等的实数根；②﹣1＜m＜2；③将该抛物线向左平移2个单位，再向下平移2个单位，所得抛物线解析式为y＝﹣（x+1）²+m；④点A关于直线x＝1的对称点为C，点D、E分别在x轴和y轴上，当m＝1时，四边形BCDE周长的最小值为 $\sqrt{34} + \sqrt{2}$ ．其中正确的个数是（　　）

A、1 B、2 C、3 D、4

查看试题解析
9. 已知△ABC为等腰三角形，若BC＝6，且AB，AC为方程x²﹣8x+m＝0两根，则m的值等于（　　）

A、12 B、16 C、﹣12或﹣16 D、12或16

查看试题解析
10. 如图在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B₁、C₁处，点B₁在x轴上，再将△AB₁C₁绕点B₁顺时针旋转到△A₁B₁C₂的位置，点C₂在x轴上，将△A₁B₁C₂绕点C₂顺时针旋转到△A₂B₂C₂的位置，点A₂在x轴上，依次进行下去…若点A（ $\frac{3}{2}$ ，0），B（0，2），则点B₂₀₁₈的坐标为（）

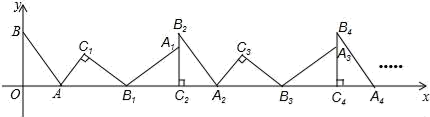A、（6048，0） B、（6054，0） C、（6048，2） D、（6054，2）

查看试题解析

二、填空题

11. 在 $Δ A B C$ 中，如果 $∠ A : ∠ B : ∠ C = 1 : 2 : 3$ ，根据三角形按角进行分类，这个三角形是三角形． $∠ A =$ 度．

查看试题解析
12. x²﹣4y²＝（x+）（x﹣）

查看试题解析
13. 如图，圆锥的底面圆的半径是3，其母线长是9，则圆锥侧面展开图的扇形的圆心角度数是 °．

查看试题解析
14. 若一次函数y＝kx+2的图象，y随x的增大而增大，并与x轴、y轴所围成的三角形的面积为2，则k＝．

查看试题解析
15. 三角形三边的长是2、5、m，则 $\sqrt{{(m - 3)}^{2}} + \sqrt{{(m - 7)}^{2}}$ ＝．

查看试题解析
16. 如图，以平行四边形ABCO的顶点O为原点，边OC所在直线为x轴，建立平面直角坐标系，顶点C的坐标是（2，0），tan∠AOC＝2，过点A的反比例函数 $y = \frac{k}{x}$ 的图象过BC边的中点D，则k的值是．

查看试题解析

三、解答题

17. 解方程组：

(1)、 ${\begin{array}{l} x + y = 2 \\ 2 x - \frac{1}{3} y = \frac{5}{3} \end{array}$ ；

(2)、 ${\begin{array}{l} 2 x - y = - 4 \\ 4 x - 5 y = - 23 \end{array}$ ．

查看试题解析
18. 如图，在菱形ABCD中，BE⊥CD于点E，DF⊥BC于点F．

(1)、求证：BE＝DF；

(2)、若∠A＝45°，求 $\frac{D E}{C E}$ 的值．

查看试题解析
19. 先化简，再求值：（ $\frac{x^{2}}{x - 1}$ +x﹣1）÷ $\frac{1}{1 - x}$ ，其中x满足x²﹣x﹣5＝0．

查看试题解析
20. 如图，有大小质地相同仅颜色不同的两双拖鞋（分左、右脚）共四只，放置于地板上（分别用A₁ ， A₂ ， B₁ ， B₂表示）．

(1)、若已经拿到左脚拖鞋A₁ ，再从两只右脚拖鞋中随机取一只，则恰好匹配成双相同颜色的拖鞋的概率是．

(2)、若从这四只拖鞋中随机取出两只，利用画树状图或列表的方法求恰好取出一双相同颜色的拖鞋的概率．

查看试题解析
21. 某医疗器械生产厂家接到A型口罩40万只和B型口罩45万只的订单，该工厂有甲、乙两个车间，甲车间生产A型口罩，乙车间生产B型口罩，已知乙车间每天生产的口罩数量比甲车间每天生产的口罩数量多80%，结果乙车间比甲车间提前3天完成订单任务．求甲车间每天生产A型口罩多少万只?

查看试题解析
22. 如图，在Rt△ABC中，∠ABC＝90°，直角顶点B位于x轴的负半轴，点A（0，﹣2），斜边AC交x轴于点D，且D（1，0），BC与y轴交于点E，y轴平分∠BAC，反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象经过点C．

(1)、直接写出点B的坐标；

(2)、求y＝ $\frac{k}{x}$ （x＞0）的函数表达式．

查看试题解析
23. 边长为4的正方形ABCD中，EM是BC边的垂直平分线，连接AE，⊙O经过A，D两点且与BC边相切于点E，动点P在射线BC上且在点C的右侧，动点Q位于直线BC的上方，连接PQ．

(1)、请用无刻度直尺和圆规在图1中作出⊙O并直接写出⊙O的半径r＝；（不写作法，保留痕迹）

(2)、设OE交BQ于点F，若PQ＝CP＝5a，△PCQ的面积为10a² ，求 $\frac{O F}{F E}$ 的值（用含a的代数式表示），并直接写出a的最大值．

查看试题解析
24. 数学来源于生活，数学之美无处不在，在几何图形中，最美的角是45°，最美的直角三角形是等腰直角三角形，我们把45°的角称为一中美角，最美的等腰直角三角形称为一中美三角．根据该约定，完成下列问题：

(1)、如图1，已知正方形ABCD中O是对角线AC上一动点，过O作OP⊥OD，垂足为O，交BC边于P，△POD是否为一中美三角，并说明理由；

(2)、如图2，在平面直角坐标系中，点A（﹣2，0），点B（0，2），点P在第二象限内，且在直线y＝﹣2x﹣2上，若△ABP恰好构成一中美三角，求出此时P点的坐标；

(3)、如图3，若二次函数y＝﹣x²+2x+3的图象与x轴交于A、B两点，与y轴交于点C，P为第二象限上的点，在直线AC上，且∠OPB恰好构成一中美角；Q为x轴上方抛物线上的一动点，令Q点横坐标为m（0＜m＜3），当m为何值时，△PBQ的面积最大，求出此时Q点坐标和最大面积．

查看试题解析
25. 如图，⊙O的弦AC与BD互相垂直于点E，OA交ED于点F．

(1)、如图（1），求证：∠BAC＝∠OAD；

(2)、如图（2），当AC＝CD时，求证：AB＝BF；

(3)、如图（3），在（2）的条件下，点P，Q在CD上，点P为CQ中点，∠POQ＝∠OFD，DF＝EC，DQ＝6，求AB的长．

查看试题解析