河北省石家庄市新华区2022年初中毕业年级质量监测数学试题
试卷更新日期:2022-04-26 类型:中考模拟
一、单选题
-
1. 如果水库的水位高于标准水位2 m时,记作+2 m,那么低于标准水位1 m时,应记作( )A、-1 m B、0m C、+1 m D、-2 m2. 到直线l的距离等于5 cm的点有( )A、0个 B、1个 C、无数个 D、无法确定3. 下列式子化简后的结果为x6的是( )A、x3+x3 B、x3•x3 C、(x3)3 D、x12÷x24. 如图是由棱长为1的几个正方体组成的几何体的三视图,则这个几何体的体积是( )
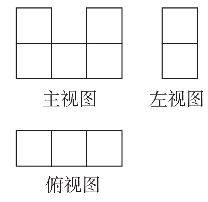 A、3 B、4 C、5 D、65. 2022年3月5日,在第十三届全国人民代表大会第五次会议上,李克强总理在政府工作报告中指出:2021年我国国内生产总值达到114万亿元,增长8.1%.将114万亿用科学记数法可表示为( )A、 B、 C、 D、6. 如图,已知四边形ABCD的面积为8cm2 , AB∥CD,AB=CD,E是AB的中点,那么△AEC的面积是( )
A、3 B、4 C、5 D、65. 2022年3月5日,在第十三届全国人民代表大会第五次会议上,李克强总理在政府工作报告中指出:2021年我国国内生产总值达到114万亿元,增长8.1%.将114万亿用科学记数法可表示为( )A、 B、 C、 D、6. 如图,已知四边形ABCD的面积为8cm2 , AB∥CD,AB=CD,E是AB的中点,那么△AEC的面积是( ) A、 B、 C、 D、7. 把多项式分解因式的结果为( )A、 B、 C、 D、8. 设A,B,C均为多项式,小方同学在计算“A﹣B”时,误将符号抄错而计算成了“A+B”,得到结果是C,其中A=x2+x﹣1,C=x2+2x,那么A﹣B=( )A、x2﹣2x B、x2+2x C、﹣2 D、﹣2x9. 如图,在的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有( )
A、 B、 C、 D、7. 把多项式分解因式的结果为( )A、 B、 C、 D、8. 设A,B,C均为多项式,小方同学在计算“A﹣B”时,误将符号抄错而计算成了“A+B”,得到结果是C,其中A=x2+x﹣1,C=x2+2x,那么A﹣B=( )A、x2﹣2x B、x2+2x C、﹣2 D、﹣2x9. 如图,在的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有( ) A、2个 B、3个 C、4个 D、5个10. 已知三个数 ,-3, ,它们的大小关系是( )A、 B、 C、 D、11. 将一枚质地均匀的骰子连续投掷两次,记投掷两次的正面数字之和为S,则下面关于事件S发生的概率说法不正确的是( )A、 B、 C、 D、12. 若关于x的方程 的解为正数,则m的取值范围是( )A、m<6 B、m>6 C、m<6且m≠0 D、m>6且m≠813. 对于二次函数所具有的性质,下列描述正确的是( )A、图象与x轴的交点坐标是 B、图象开口向上 C、对称轴是直线 D、在对称轴的左侧y随x的增大而增大14. 如图,在的正方形网格图中,A、B、C为格点,则的值为( )
A、2个 B、3个 C、4个 D、5个10. 已知三个数 ,-3, ,它们的大小关系是( )A、 B、 C、 D、11. 将一枚质地均匀的骰子连续投掷两次,记投掷两次的正面数字之和为S,则下面关于事件S发生的概率说法不正确的是( )A、 B、 C、 D、12. 若关于x的方程 的解为正数,则m的取值范围是( )A、m<6 B、m>6 C、m<6且m≠0 D、m>6且m≠813. 对于二次函数所具有的性质,下列描述正确的是( )A、图象与x轴的交点坐标是 B、图象开口向上 C、对称轴是直线 D、在对称轴的左侧y随x的增大而增大14. 如图,在的正方形网格图中,A、B、C为格点,则的值为( ) A、 B、 C、 D、15. 用表示a、b两数中较大的数,如 . 若函数y=max{1,(x>0)},则y与x之间的函数图象大致为( )A、
A、 B、 C、 D、15. 用表示a、b两数中较大的数,如 . 若函数y=max{1,(x>0)},则y与x之间的函数图象大致为( )A、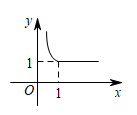 B、
B、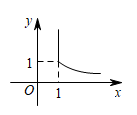 C、
C、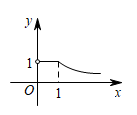 D、
D、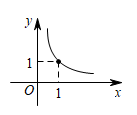 16. 如图,将一张矩形纸片折叠,使点A与点C重合,再展开,折痕EF交对角线BD于点O,分别交BC,AD边于E,F两点,连接AE和CF.当时,在下列结论中:
16. 如图,将一张矩形纸片折叠,使点A与点C重合,再展开,折痕EF交对角线BD于点O,分别交BC,AD边于E,F两点,连接AE和CF.当时,在下列结论中:①△AEF是等边三角形;
②四边形AECF是菱形;
③;
④;
⑤射线CF是的三等分线.正确的个数有( )个.
 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
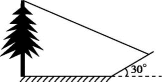
17. 若 , 则 . .18. 小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米,垂直于地面放置的标杆在地面上的影长为2米,则树的高度为 .
 19. 将长是宽2倍的矩形作如下分割:
19. 将长是宽2倍的矩形作如下分割:第1次:将矩形分割成2个全等的正方形(如图1);
第2次:将左边的正方形分割成4个全等的正方形(如图2);
第3次:将左上角的正方形分割成4个全等的正方形(如图3);
……
按此方式分割下去,则第n次时得到的所有正方形的个数为;当正方形的个数为2022个时,分割的次数为次.

三、解答题
-
20. 已知:如图,数轴上点A所表示的数为4,点A关于原点的对称点为点B,设点B所表示的数为x.
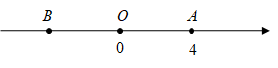 (1)、直接写出:;(2)、求的值.21. 某县水资源短缺,为了提高人们的节水意识,决定对县城内居民用水采取阶梯式收费,需要确定用水量的标准,并对超出这个标准的部分按1.5倍价格收费.在制定标准前,县政府对居民生活用水情况进行了随机抽样调查,获得50个家庭去年月均用水量(单位:吨)的数据如下:
(1)、直接写出:;(2)、求的值.21. 某县水资源短缺,为了提高人们的节水意识,决定对县城内居民用水采取阶梯式收费,需要确定用水量的标准,并对超出这个标准的部分按1.5倍价格收费.在制定标准前,县政府对居民生活用水情况进行了随机抽样调查,获得50个家庭去年月均用水量(单位:吨)的数据如下:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.6 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5通过对调查数据的整理,得到图1和图2两幅不完整的统计图表.
 (1)、将频数分布表和频数分布直方图补充完整;(2)、从直方图中你能得到什么信息?(写出两条即可)(3)、要使60%的家庭收费不受影响,你觉得家庭月均用水量的标准应该定为多少?为什么?22. 如图,在△ABC中,AB=AC,以AC为直径的半圆O与边BC相交于点D,DE⊥AB,垂足为E.
(1)、将频数分布表和频数分布直方图补充完整;(2)、从直方图中你能得到什么信息?(写出两条即可)(3)、要使60%的家庭收费不受影响,你觉得家庭月均用水量的标准应该定为多少?为什么?22. 如图,在△ABC中,AB=AC,以AC为直径的半圆O与边BC相交于点D,DE⊥AB,垂足为E. (1)、求证:点D是BC的中点;(2)、判断DE与⊙O的位置关系,并证明你的结论;(3)、若⊙O的直径为18,BC=12,求DE的长.23. 已知:如图,直线与x轴、y轴分别相交于A、B两点,与双曲线相交于P(m,1)、Q( , n)两点,连接OP、OQ.
(1)、求证:点D是BC的中点;(2)、判断DE与⊙O的位置关系,并证明你的结论;(3)、若⊙O的直径为18,BC=12,求DE的长.23. 已知:如图,直线与x轴、y轴分别相交于A、B两点,与双曲线相交于P(m,1)、Q( , n)两点,连接OP、OQ. (1)、求双曲线的函数表达式;(2)、求△OPQ的面积;(3)、若点M是坐标轴上的动点,当的值最小时,请你直接写出点M的坐标.24. 如图1,在等边△ABC中,AB=2,过点C作CE⊥AB,垂足为E,P为CE上任意一点(点P与点C不重合),把AP绕点A顺时针旋转60°,点P的对应点为点D,分别连接BD、PD、ED.
(1)、求双曲线的函数表达式;(2)、求△OPQ的面积;(3)、若点M是坐标轴上的动点,当的值最小时,请你直接写出点M的坐标.24. 如图1,在等边△ABC中,AB=2,过点C作CE⊥AB,垂足为E,P为CE上任意一点(点P与点C不重合),把AP绕点A顺时针旋转60°,点P的对应点为点D,分别连接BD、PD、ED. (1)、求证:BD=CP;(2)、当点P与点E重合时,请你按照题干要求,在图2中作出图形,并延长CE交BD于点F,求出BF的长;(3)、直接写出线段DE长度的最小值.25. 小亮创办了一个微店商铺,营销一款小型LED护眼台灯,成本是20元/盏,在“双十一”前20天进行了网上销售后发现,该台灯的日销售量p(盏)与时间x(天)之间满足一次函数关系,且第1天销售了78盏,第2天销售了76盏.护眼台灯的销售价格y(元/盏)与时间x(天)之间符合函数关系式( , 且x为整数).(1)、求日销售量p(盏)与时间x(天)之间的函数关系式;(2)、在这20天中,哪天的日销售利润最大?最大日销售利润是多少?(3)、“双十一”当天,小亮采用如下促销方式:销售价格比前20天中最高日销售价格降低a元;日销售量比前20天最高日销售量提高了7a盏;日销售利润比前20天中的最大日销售利润多了30元,求a的值.(注:销售利润=售价-成本).26. 如图,在平面直角坐标系中,过点A(8,6)作AB⊥y轴,垂足为B;动点P从原点O出发,以每秒3个单位长度的速度沿x轴正方向运动;动点Q从点A同时出发,以每秒2个单位长度的速度沿AB向终点B运动,连接PQ.设运动的时间为ts.
(1)、求证:BD=CP;(2)、当点P与点E重合时,请你按照题干要求,在图2中作出图形,并延长CE交BD于点F,求出BF的长;(3)、直接写出线段DE长度的最小值.25. 小亮创办了一个微店商铺,营销一款小型LED护眼台灯,成本是20元/盏,在“双十一”前20天进行了网上销售后发现,该台灯的日销售量p(盏)与时间x(天)之间满足一次函数关系,且第1天销售了78盏,第2天销售了76盏.护眼台灯的销售价格y(元/盏)与时间x(天)之间符合函数关系式( , 且x为整数).(1)、求日销售量p(盏)与时间x(天)之间的函数关系式;(2)、在这20天中,哪天的日销售利润最大?最大日销售利润是多少?(3)、“双十一”当天,小亮采用如下促销方式:销售价格比前20天中最高日销售价格降低a元;日销售量比前20天最高日销售量提高了7a盏;日销售利润比前20天中的最大日销售利润多了30元,求a的值.(注:销售利润=售价-成本).26. 如图,在平面直角坐标系中,过点A(8,6)作AB⊥y轴,垂足为B;动点P从原点O出发,以每秒3个单位长度的速度沿x轴正方向运动;动点Q从点A同时出发,以每秒2个单位长度的速度沿AB向终点B运动,连接PQ.设运动的时间为ts. (1)、当t为何值时,PQ取得最小值;(2)、当PQ=2时,求t的值;(3)、在备用图中,连接OA交PQ于点C,试问:随着两个动点P、Q的运动,点C的位置是否变化?若不变化,请求出点C的坐标;若变化,请说明理由.
(1)、当t为何值时,PQ取得最小值;(2)、当PQ=2时,求t的值;(3)、在备用图中,连接OA交PQ于点C,试问:随着两个动点P、Q的运动,点C的位置是否变化?若不变化,请求出点C的坐标;若变化,请说明理由.