河北省邯郸市2022年中考模拟数学试题 (二)
试卷更新日期:2022-04-26 类型:中考模拟
一、单选题
-
1. -2是2的( )A、相反数 B、倒数 C、绝对值 D、算术平方根2. 分式方程的解为( )A、 B、 C、 D、3. 如图是五个相同的正方体组成的一个几何体,它的左视图是( )
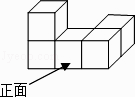 A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,用平行四边形纸条沿对边AB、CD上的点E、F所在的直线折成V字形图案,已知图中∠1=56°,则∠2的度数为( )
4. 如图,用平行四边形纸条沿对边AB、CD上的点E、F所在的直线折成V字形图案,已知图中∠1=56°,则∠2的度数为( ) A、56° B、66° C、68° D、112°5. 如图,点A是反比例函数 (x<0)的图象上的一点,过点A作平行四边形ABCD,使B,C在x轴上,点D在y轴上,则平行四边形ABCD的面积为( )
A、56° B、66° C、68° D、112°5. 如图,点A是反比例函数 (x<0)的图象上的一点,过点A作平行四边形ABCD,使B,C在x轴上,点D在y轴上,则平行四边形ABCD的面积为( ) A、1 B、3 C、6 D、126. 下列说法中正确的是( )A、三角形三条角平分线的交点到三个顶点的距离相等 B、三角形三条角平分线的交点到三边的距离相等 C、三角形三条中线的交点到三个顶点的距离相等 D、三角形三条中线的交点到三边的距离相等7. 如图,在四边形ABCD中,AC与BD相交于点O , ∠BAD=90°,BO=DO , 那么添加下列一个条件后,仍不能判定四边形ABCD是矩形的是( )
A、1 B、3 C、6 D、126. 下列说法中正确的是( )A、三角形三条角平分线的交点到三个顶点的距离相等 B、三角形三条角平分线的交点到三边的距离相等 C、三角形三条中线的交点到三个顶点的距离相等 D、三角形三条中线的交点到三边的距离相等7. 如图,在四边形ABCD中,AC与BD相交于点O , ∠BAD=90°,BO=DO , 那么添加下列一个条件后,仍不能判定四边形ABCD是矩形的是( )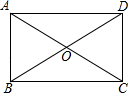 A、∠ABC=90° B、∠BCD=90° C、AB=CD D、AB∥CD8. 根据如图所示的程序计算:若输入自变量x的值为 ,则输出的结果是( )
A、∠ABC=90° B、∠BCD=90° C、AB=CD D、AB∥CD8. 根据如图所示的程序计算:若输入自变量x的值为 ,则输出的结果是( ) A、 B、 C、 D、9. 将弧长为2πcm、圆心角为120°的扇形围成一个圆锥的侧面,则这个圆锥的高是( )A、 cm B、2 cm C、2cm D、 cm10. 若整数a使关于x的分式方程﹣2=有整数解,则符合条件的所有a之和为( )A、7 B、11 C、12 D、1311. 若用“*”表示一种运算规则,我们规定:a*b=ab﹣a+b,如:3*2=3×2﹣3+2=5.以下说法中不正确的是( )A、不等式(﹣2)*(3﹣x)<2的解集是x<3 B、函数y=(x+2)*x的图象与x轴有两个交点 C、在实数范围内,无论a取何值,代数式a*(a+1)的值总为正数 D、方程(x﹣2)*3=5的解是x=512. 在平面直角坐标系中,二次函数y=a(x−h)2(a≠0)的图象可能是( )A、
A、 B、 C、 D、9. 将弧长为2πcm、圆心角为120°的扇形围成一个圆锥的侧面,则这个圆锥的高是( )A、 cm B、2 cm C、2cm D、 cm10. 若整数a使关于x的分式方程﹣2=有整数解,则符合条件的所有a之和为( )A、7 B、11 C、12 D、1311. 若用“*”表示一种运算规则,我们规定:a*b=ab﹣a+b,如:3*2=3×2﹣3+2=5.以下说法中不正确的是( )A、不等式(﹣2)*(3﹣x)<2的解集是x<3 B、函数y=(x+2)*x的图象与x轴有两个交点 C、在实数范围内,无论a取何值,代数式a*(a+1)的值总为正数 D、方程(x﹣2)*3=5的解是x=512. 在平面直角坐标系中,二次函数y=a(x−h)2(a≠0)的图象可能是( )A、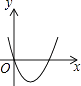 B、
B、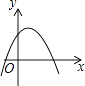 C、
C、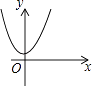 D、
D、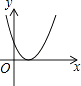 13. 正方形ABCD的边长为2,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为( )
13. 正方形ABCD的边长为2,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为( )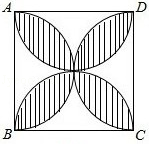 A、 B、 C、 D、14. 如图,在直角坐标系中,有菱形 , 点的坐标是 ,双曲线 经过点 ,且 ,则k的值为( )
A、 B、 C、 D、14. 如图,在直角坐标系中,有菱形 , 点的坐标是 ,双曲线 经过点 ,且 ,则k的值为( ) A、40 B、48 C、64 D、8015. 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点A , B , C . 现有下面四个推断:①抛物线开口向下;②当x=-2时,y取最大值;③当m<4时,关于x的一元二次方程ax2+bx+c=m必有两个不相等的实数根;④直线y=kx+c(k≠0)经过点A , C , 当kx+c> ax2+bx+c时,x的取值范围是-4<x<0;其中推断正确的是 ( )
A、40 B、48 C、64 D、8015. 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点A , B , C . 现有下面四个推断:①抛物线开口向下;②当x=-2时,y取最大值;③当m<4时,关于x的一元二次方程ax2+bx+c=m必有两个不相等的实数根;④直线y=kx+c(k≠0)经过点A , C , 当kx+c> ax2+bx+c时,x的取值范围是-4<x<0;其中推断正确的是 ( )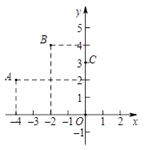 A、①② B、①③ C、①③④ D、②③④
A、①② B、①③ C、①③④ D、②③④二、填空题
-
16. 下列各式一定成立的是 .
①a2=(﹣a)2;②a3=(﹣a)3;③﹣a2=|﹣a2|;④a3=|a3|.
17. 比较大小: 1.(选填“<”“>”或“=”)18. 若a﹣b=2,a+b=3,则a2﹣b2= .19. 如图,在平行四边形ABCD中, , , 垂足分别为E、F, , , , 则平行四边形ABCD的面积为 .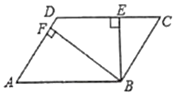 20. 如图,在△ABC中,AC=BC , ∠ACB=100°,点D在线段AB上运动(D不与A , B重合),连接CD , 作∠CDE=40°,DE交BC于点E . 若△CDE是等腰三角形,则∠ADC的度数是 .
20. 如图,在△ABC中,AC=BC , ∠ACB=100°,点D在线段AB上运动(D不与A , B重合),连接CD , 作∠CDE=40°,DE交BC于点E . 若△CDE是等腰三角形,则∠ADC的度数是 .
三、解答题
-
21. 计算:(1)、(2)、(π-)0+|-1|+()-1-2sin45°.22. 为迎接十二运,某校开设了A:篮球,B:毽球,C:跳绳,D:健美操四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学必须选择而且只能在4中体育活动中选择一种).将数据进行整理并绘制成以下两幅统计图(未画完整).
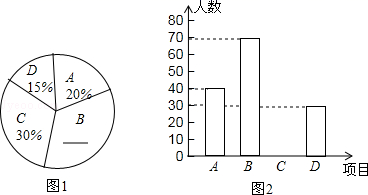 (1)、这次调查中,一共查了名学生:(2)、请补全两幅统计图:(3)、若有3名最喜欢毽球运动的学生,1名最喜欢跳绳运动的学生组队外出参加一次联谊互活动,欲从中选出2人担任组长(不分正副),求两人均是最喜欢毽球运动的学生的概率.23. 如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据: ≈1.414, ≈1.732)
(1)、这次调查中,一共查了名学生:(2)、请补全两幅统计图:(3)、若有3名最喜欢毽球运动的学生,1名最喜欢跳绳运动的学生组队外出参加一次联谊互活动,欲从中选出2人担任组长(不分正副),求两人均是最喜欢毽球运动的学生的概率.23. 如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据: ≈1.414, ≈1.732) 24. 如图,在△ABC中,AB=AC,以AB为直径作⊙O交于BC于D,DE⊥AC于E.
24. 如图,在△ABC中,AB=AC,以AB为直径作⊙O交于BC于D,DE⊥AC于E. (1)、求证:DE是⊙O的切线;(2)、若AB=13,BC=10,求△DEC的面积.25. 如图,直线y=kx+b(k≠0)与双曲线y= (m≠0)交于点A(﹣ ,2),B(n,﹣1).
(1)、求证:DE是⊙O的切线;(2)、若AB=13,BC=10,求△DEC的面积.25. 如图,直线y=kx+b(k≠0)与双曲线y= (m≠0)交于点A(﹣ ,2),B(n,﹣1). (1)、求直线与双曲线的解析式.
(1)、求直线与双曲线的解析式.
(2)、点P在x轴上,如果S△ABP=3,求点P的坐标.
26. 请认真阅读下面的数学小探究系列,完成所提出的问题: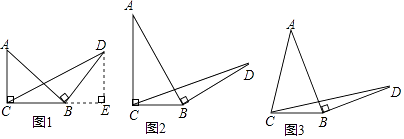 (1)、探究1:如图1,在等腰直角三角形ABC中, , ,将边AB绕点B顺时针旋转 得到线段BD,连接 求证: 的面积为 提示:过点D作BC边上的高DE,可证 ≌
(1)、探究1:如图1,在等腰直角三角形ABC中, , ,将边AB绕点B顺时针旋转 得到线段BD,连接 求证: 的面积为 提示:过点D作BC边上的高DE,可证 ≌
(2)、探究2:如图2,在一般的 中, , ,将边AB绕点B顺时针旋转 得到线段BD,连接 请用含a的式子表示 的面积,并说明理由.
(3)、探究3:如图3,在等腰三角形ABC中, , ,将边AB绕点B顺时针旋转 得到线段BD,连接 试探究用含a的式子表示 的面积,要有探究过程.27. 如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B两点(点A在点B的左侧),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m. (1)、求抛物线的解析式;(2)、当点P在线段OB上运动时,求线段MN的最大值;(3)、是否存在点P,使得以点C、O、M、N为顶点的四边形是平行四边形?若存在,请直接写出m的值;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、当点P在线段OB上运动时,求线段MN的最大值;(3)、是否存在点P,使得以点C、O、M、N为顶点的四边形是平行四边形?若存在,请直接写出m的值;若不存在,请说明理由.