河北省邯郸市武安市2022年中考一模数学试题
试卷更新日期:2022-04-26 类型:中考模拟
一、单选题
-
1. 经过直线 l 外一点O的四条直线中,与直线l相交的直线至少有( )
 A、1条 B、2条 C、3条 D、4条2. 下列运算结果正确的是( )A、 B、 C、 D、3. 与结果相同的是( )A、 B、 C、 D、4. 某同学粗心大意,分解因式时,把等式中的两个数弄污了,那么你认为式子中的和所对应的一组数是( )A、9,3 B、81,3 C、81,9 D、27,35. 将0.00000012用科学记数法表示为 , 则n的值为( )A、 B、 C、7 D、86. 一个正方体的六个面分别标有六个不同的点数,其展开图如下所示,则该正方体可能是( ).
A、1条 B、2条 C、3条 D、4条2. 下列运算结果正确的是( )A、 B、 C、 D、3. 与结果相同的是( )A、 B、 C、 D、4. 某同学粗心大意,分解因式时,把等式中的两个数弄污了,那么你认为式子中的和所对应的一组数是( )A、9,3 B、81,3 C、81,9 D、27,35. 将0.00000012用科学记数法表示为 , 则n的值为( )A、 B、 C、7 D、86. 一个正方体的六个面分别标有六个不同的点数,其展开图如下所示,则该正方体可能是( ).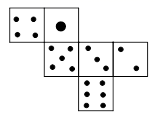 A、
A、 B、
B、 C、
C、 D、
D、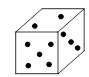 7. 如图1,矩形纸片中, , , 要在矩形纸片内折出一个菱形.现有两种方案:
7. 如图1,矩形纸片中, , , 要在矩形纸片内折出一个菱形.现有两种方案:甲:如图2,取两组对边中点的方法折出菱形 .
乙:如图3,沿矩形的对角线折出 , 的方法得到菱形 . 下列说法正确的是( )
 A、甲、乙折出的菱形面积一样大 B、乙折出的四边形不是菱形 C、甲折出的菱形面积大 D、乙折出的菱形面积大8. 如图,在正方形网格中,△ABC和△DEF相似,则关于位似中心与相似比叙述正确的是( )
A、甲、乙折出的菱形面积一样大 B、乙折出的四边形不是菱形 C、甲折出的菱形面积大 D、乙折出的菱形面积大8. 如图,在正方形网格中,△ABC和△DEF相似,则关于位似中心与相似比叙述正确的是( )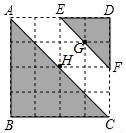 A、位似中心是点B,相似比是2:1 B、位似中心是点D,相似比是2:1 C、位似中心在点G,H之间,相似比为2:1 D、位似中心在点G,H之间,相似比为1:29. 若取1.71,计算的结果是( )A、71 B、171 C、1.71 D、17.110. 如图,已知正六边形 的边长为1,分别以其对角线 、 为边作正方形,则两个阴影部分的面积差a-b的值为( )
A、位似中心是点B,相似比是2:1 B、位似中心是点D,相似比是2:1 C、位似中心在点G,H之间,相似比为2:1 D、位似中心在点G,H之间,相似比为1:29. 若取1.71,计算的结果是( )A、71 B、171 C、1.71 D、17.110. 如图,已知正六边形 的边长为1,分别以其对角线 、 为边作正方形,则两个阴影部分的面积差a-b的值为( ) A、0 B、2 C、1 D、11. 如图,将数轴上-4与8两点间的线段六等分,五个等分点所对应的数依次为 , , , , , 则下列结论不正确的是( )
A、0 B、2 C、1 D、11. 如图,将数轴上-4与8两点间的线段六等分,五个等分点所对应的数依次为 , , , , , 则下列结论不正确的是( ) A、 B、 C、 D、12. 只把分式中的m,n同时扩大为原来的3倍后,分式的值也不会变,则此时a的值可以是下列中的( )A、2 B、 C、 D、13. 定理:三角形的内角和等于 .
A、 B、 C、 D、12. 只把分式中的m,n同时扩大为原来的3倍后,分式的值也不会变,则此时a的值可以是下列中的( )A、2 B、 C、 D、13. 定理:三角形的内角和等于 .已知:的三个内角为 , , .
求证: .
证法1
证法2
如图1,延长到点D,则(三角形的一个外角等于和它不相邻的两个内角的和).
∵(平角的定义),
∴(等量代换).

如图2,过点作 , ∵ ,
(两直线平行,内错角相等),
(两直线平行,内错角相等),
又∵(平角定义),
∴(等量代换).

下列说法正确的是( )
A、证法1采用了从特殊到一般的方法证明了该定理 B、证法1用合理的推理证明了该定理 C、证法2还需证明其他形状的三角形,该定理的证明过程才完整 D、证法2用严谨的推理证明了该定理14. 小明得到数学课外兴趣小组成员的年龄情况统计如下表:年龄(岁)
13
14
15
16
人数(人)
2
15
x
那么对于不同x的值,则下列关于年龄的统计量不会发生变化的是( )
A、平均数、方差 B、中位数、方差 C、平均数、中位数 D、众数、中位数15. 定义:如果一元二次方程满足 , 那么就称这个方程为“凤凰方程”.已知是“凤凰方程”,且有两个相等的实数根,则a与c的关系是( )A、 B、 C、 D、16. 如图,已知 , 用尺规按照下面步骤操作:①作线段的垂直平分线;②作线段的垂直平分线 , 交于点O;③以O为圆心,长为半径作 .
结论Ⅰ:点O是的内心.
结论Ⅱ: .
对于结论Ⅰ和结论Ⅱ,下列判断正确的是( )
 A、Ⅰ和Ⅱ都对 B、Ⅰ和Ⅱ都不对 C、Ⅰ不对Ⅱ对 D、Ⅰ对Ⅱ不对
A、Ⅰ和Ⅱ都对 B、Ⅰ和Ⅱ都不对 C、Ⅰ不对Ⅱ对 D、Ⅰ对Ⅱ不对二、填空题
-
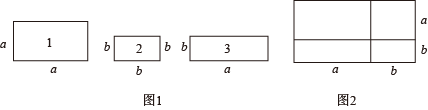
17. 嘉嘉同学动手剪了如图1所示的正方形与矩形纸片若干张.
 (1)、他用1张1号、1张2号和2张3号卡片拼出一个新的图形(如图2).根据这个图形的面积关系写出一个你所熟悉的乘法公式,这个乘法公式是 .(2)、如果要拼成一个长为 , 宽为的大长方形,则需要3号卡片张.18. 定义:在平面直角坐标系中,如果将点P绕点旋转得到点Q,那么称线段为“拓展带”,点Q为点P的“拓展带”.(1)、当时,点的“拓展带”坐标为 .(2)、如果 , 当点的“拓展带”N在函数的图象上时,t的值为 .
(1)、他用1张1号、1张2号和2张3号卡片拼出一个新的图形(如图2).根据这个图形的面积关系写出一个你所熟悉的乘法公式,这个乘法公式是 .(2)、如果要拼成一个长为 , 宽为的大长方形,则需要3号卡片张.18. 定义:在平面直角坐标系中,如果将点P绕点旋转得到点Q,那么称线段为“拓展带”,点Q为点P的“拓展带”.(1)、当时,点的“拓展带”坐标为 .(2)、如果 , 当点的“拓展带”N在函数的图象上时,t的值为 .三、解答题
-
19. 有个补充运算符号的游戏:在“”中的每个内,填入+,﹣,×,÷中的某一个(可重复使用),然后计算结果.(1)、计算:(直接写出结果);(2)、若 , 请推算内的符号应是什么;(3)、请在内填上×,÷中的一个,使计算更加简便,然后计算.
计算: .
20. 已知某公司采购A,B两种不同洗手液共138瓶,设采购了A种洗手液x瓶.(1)、嘉嘉说:“买到的B种洗手液的瓶数是A种的三倍.”琪琪由此列出方程: , 请用列出的方程判断嘉嘉的说法是否正确;(2)、采购人员说:“B种洗手液比A种至少多32瓶.”请通过列不等式的方法说明A种洗手液最多有几瓶.21. 在一不透明的袋子中装有四张标有数字2,3,4,5的卡片,这些卡片除数字外其余均相同.嘉琪按照一定的规则抽出两张卡片,并把卡片上的数字相加.如图是他所画树状图的一部分. (1)、①嘉琪第一次抽到标有数字为奇数的卡片的概率为 .
(1)、①嘉琪第一次抽到标有数字为奇数的卡片的概率为 .②由图分析,该游戏规则是:第一次从袋子中随机抽出一张卡片后(选填“放回”或“不放回”),第二次随机再抽出一张卡片;
(2)、补全树状图,并求嘉琪两次抽到卡片上的数字之和为偶数的概率.22. 甲、乙两名同学沿直线进行登山,甲、乙沿相同的路线同时从山脚出发到达山顶甲同学到达山顶休息后再沿原路下山,他们离山脚的距离随时间(h)变化的图象如图所示,根据图象中的有关信息回答下列问题: (1)、甲同学上山过程中与t的函数解析式为;点D的坐标为 .(2)、若甲同学下山时在点F处与乙同学相遇,此时点F与山顶的距离为 .
(1)、甲同学上山过程中与t的函数解析式为;点D的坐标为 .(2)、若甲同学下山时在点F处与乙同学相遇,此时点F与山顶的距离为 .①求甲同学下山过程中S与t的函数解析式;
②相遇后甲、乙各自继续下山和上山,求当乙到达山顶时,甲与乙的距离是多少千米.
23. 如图1,足球场上守门员李伟在O处抛出一高球,球从离地面处的点A飞出,其飞行的最大高度是 , 最高处距离飞出点的水平距离是 , 且飞行的路线是抛物线的一部分.以点O为坐标原点,竖直向上的方向为y轴的正方向,球飞行的水平方向为x轴的正方向建立坐标系,并把球看成一个点(参考数据:取 , ) (1)、求足球的飞行高度与飞行水平距离之间的函数关系式;(2)、在没有队员干扰的情况下,球飞行的最远水平距离是多少?(3)、若对方一名的队员在距落点的点H处,跃起进行拦截,则这名队员能拦到球吗?(4)、如图2,在(2)的情况下,若球落地后又一次弹起,据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半,那么足球弹起后,会弹出多远?24. 如图,在中, , , , 半圆O的直径 . 点E与点C重合,半圆O以的速度从左向右移动,在运动过程中,点D、E始终在所在的直线上.设运动时间为 , 半圆O与的重叠部分的面积为 .
(1)、求足球的飞行高度与飞行水平距离之间的函数关系式;(2)、在没有队员干扰的情况下,球飞行的最远水平距离是多少?(3)、若对方一名的队员在距落点的点H处,跃起进行拦截,则这名队员能拦到球吗?(4)、如图2,在(2)的情况下,若球落地后又一次弹起,据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半,那么足球弹起后,会弹出多远?24. 如图,在中, , , , 半圆O的直径 . 点E与点C重合,半圆O以的速度从左向右移动,在运动过程中,点D、E始终在所在的直线上.设运动时间为 , 半圆O与的重叠部分的面积为 . (1)、当时,设点M是半圆O上一点,点N是线段上一点,则的最大值为;的最小值为 .(2)、在平移过程中,当点O与的中点重合时,求半圆O与重叠部分的面积S;(3)、当x为何值时,半圆O与的边所在的直线相切?
(1)、当时,设点M是半圆O上一点,点N是线段上一点,则的最大值为;的最小值为 .(2)、在平移过程中,当点O与的中点重合时,求半圆O与重叠部分的面积S;(3)、当x为何值时,半圆O与的边所在的直线相切?

