广东省粤西地区2022年九年级数学一模试题

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 2022年1月28日，北京冬奥组委发布《北京冬奥会低碳管理报告（赛前）》，根据本次“绿色办奥”理念，以及疫情下筹办和举办北京冬奥会的实际情况，修订后的基准线排放量约为130.6万吨二氧化碳当量，其中“130.6万”用科学记数法表示为（）

A、 $13.06 \times 1 0^{5}$ B、 $130.6 \times 1 0^{4}$ C、 $1.306 \times 1 0^{6}$ D、 $1.306 \times 1 0^{5}$

查看试题解析
2. 如图是由6个大小相同的立方体组成的几何体，在这个几何体的三视图中，是中心对称图形的是（）

A、主视图 B、左视图 C、俯视图 D、主视图和左视图

查看试题解析
3. 下列运算中，正确的（）

A、 $3 a^{2} - a^{2} = 2$ B、 ${(a^{2})}^{3} = a^{5}$ C、 $a^{3} \cdot a^{6} = a^{9}$ D、 ${(2 a^{2})}^{2} = 2 a^{4}$

查看试题解析
4. 在一个不透明的盒子中，有六个完全相同的小球，把它们分别标号为1，2，3，3，4，4，随机摸出一个小球，摸出的小球标号为六个数字的中位数的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
5. 如图，某水库堤坝横断面迎水坡AB的坡比是1： $\sqrt{3}$ ，堤坝高BC=50m，则应水坡面AB的长度是（）

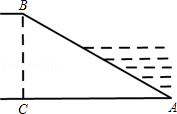A、100m B、100 $\sqrt{3}$ m C、150m D、50 $\sqrt{3}$ m

查看试题解析
6. 如图，把一个直角三角尺的直角顶点放在直尺的一边上，则 $∠ 1$ 与 $∠ 2$ 的关系为（）

A、相等 B、 $∠ 1 = 2 ∠ 2$ C、互补 D、互余

查看试题解析
7. 若正多边形的一个外角是 $7 2^{∘}$ ，则该正多边形的内角和为（）

A、 $36 0^{∘}$ B、 $54 0^{∘}$ C、 $72 0^{∘}$ D、 $90 0^{∘}$

查看试题解析
8. 如图，在 $△ A B C$ 中，分别以点A和点B为圆心，大于 $\frac{1}{2} A B$ 的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD．若 $△ A B C$ 的周长为17， $A B = 8$ ，则 $△ A C D$ 的周长为（）

A、8 B、9 C、10 D、11

查看试题解析
9. 如图，在菱形ABCD中，对角线AC，BD相交于点O，H为边AD的中点，若 $O H = \sqrt{3}$ ，则菱形ABCD的周长为（）

A、 $4 \sqrt{2}$ B、 $4 \sqrt{3}$ C、 $8 \sqrt{2}$ D、 $8 \sqrt{3}$

查看试题解析
10. 已知函数 $y = a x^{2} + a x$ 与函数 $y = \frac{a}{x} (a < 0)$ ，则它们在同一坐标系中的大致图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 如图，则 $| a |$ $| b |$ （填“>”“<”或“=”）．

查看试题解析
12. 一等腰三角形一个外角是110°，则它的底角的度数为.

查看试题解析
13. 已知实数x，y满足 $\sqrt{x - 2} + y^{2} + 2 y = - 1$ ，则 $x - y =$ ．

查看试题解析
14. 如图，位似图形由三角尺与其灯光照射下的中心投影组成，位似比为 $2 ： 5$ ，且三角尺的一边长为4cm，则投影三角尺的对应边长为cm．

查看试题解析
15. 将直线 $y = \frac{\sqrt{3}}{3} x$ 向下平移1个单位长度得到直线l，直线l与x轴交于点A，与y轴交于点B，则 $s i n ∠ A B O =$ ．

查看试题解析
16. 定义新运算“ $\otimes$ ”，规定： $x \otimes y = 2 a x + b y$ ，若 $1 \otimes (- 1) = 3$ ，则 $- 2 \otimes 2$ 的值为．

查看试题解析
17. 如图，在 $△ A B C$ 中， $A B = 5$ ， $A C = 4$ ， $B C = 3$ ，点P是AB上的任意一点，作 $P D ⊥ A C$ 于点D， $P E ⊥ C B$ 于点E，连接DE，则DE的最小值为．

查看试题解析

三、解答题

18. 计算： ${(\sqrt{3})}^{2} + 2 c o s 30 ° - {(2 - π)}^{0} + {(- \frac{1}{3})}^{- 2} + | \sqrt{3} - 3 |$ ．

查看试题解析
19. 先化简代数式： $\frac{2}{x^{3} - x} \div (\frac{1}{x - 1} - \frac{1}{x})$ ，再从0， $\sqrt{2} - 1$ ， 1三个数中选一个恰当的数作为x的值代入求值．

查看试题解析
20. 如图，四边形ABCD是平行四边形， $△ A B^{^{'}} C$ 和 $△ A B C$ 关于AC所在的直线对称，AD和 $B^{'} C$ 相交于点O，连接 $B B^{'}$ ．

(1)、请直接写出图中所有的等腰三角形（不添加字母）；

(2)、求证： $△ A B^{'} O ≌ △ C D O$ ．

查看试题解析
21. 作为全球最大的新能源汽车市场，混合动力、纯电动乃至氢燃料汽车，不但是中国出口的“金名片”和本土市场消费升级的新选择，而且正在加速成为经济高质量发展的新引擎.2022年1月，中国新能源汽车产销分别完成45.2万辆和43.1万辆，同比分别增长1.3倍和1.4倍，出口同比增长5.4倍．阳江市某中学的一个社团调查小组在本校学生中开展主题为“新能源汽车知多少”的专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为“非常了解”“比较了解”“基本了解”和“不太了解”四个等级，划分等级后的数据整理如下表：
等级
非常了解
比较了解
基本了解
不太了解
频数
25
55
18
2
频率
0.25
m
0.18
0.02

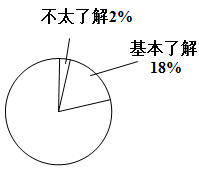(1)、本次问卷调查取样的样本容量为，表中m的值为；

(2)、根据表中的数据计算等级为“非常了解”的频数在扇形统计图（如图）中所对应的扇形的圆心角的度数，并补全扇形统计图；

(3)、若该校有学生1500人，请根据调查结果估计这些学生中“非常了解”及“比较了解”新能源汽车知识的总人数约为多少？

查看试题解析
22. 冰墩墩（如图）是2022年北京冬季奥运会的吉祥物．某商店第一次用1200元购进冰墩墩手办若干个，第二次又用相同价格购进冰墩墩饰扣若干个，已知每个冰墩墩饰扣的进价是冰墩墩手办进价的 $\frac{2}{3}$ ，购进冰墩墩手办数量比饰扣少了10个．

(1)、冰墩墩饰扣的进价是多少元？

(2)、若冰墩墩饰扣的售价要比冰墩墩手办的售价少30元，且销售完毕后获利不低于1100元，问每个冰墩墩手办的售价至少是多少元？

查看试题解析
23. 如图，已知一次函数 $y = k x + b$ 与反比例函数 $y = \frac{m}{x}$ 交于 $A (a ， - 3)$ ， $B (3 ， - 1)$ 两点．

(1)、求一次函数的解析式；

(2)、若一次函数 $y = k x + c$ 与反比例函数 $y = \frac{m}{x}$ 有一个交点，求c的值．

查看试题解析
24. 如图1，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ， AB是 $⊙ O$ 的直径， $⊙ O$ 交AC于点D，过点D的直线交BC于点E，交AB的延长线于点P，PD是 $⊙ O$ 的切线．

(1)、求证： $∠ A = ∠ P D B$ ；

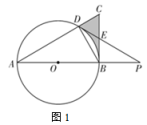(2)、若 $B P = \sqrt{3}$ ， $∠ P = ∠ P D B$ ，求图中阴影部分的周长和面积；

(3)、如图2， $\overset{⌢}{A M} = \overset{⌢}{B M}$ ，连接DM，交AB于点N，若 $t a n ∠ D M B = \frac{1}{2}$ ，求 $M N ： M D$ 的值．

查看试题解析
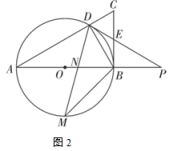25. 如图，在平面直角坐标系中，已知 $△ A O B ≌ △ C D A$ ，且 $O A = 1$ ， $B (0 ， 2)$ ，抛物线 $y = a x^{2} + a x - 4 a$ 经过点C．

(1)、求抛物线的解析式．

(2)、在抛物线（对称轴的右侧）上是否存在一点P，使△ABP是以AB为直角边的等腰直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

(3)、若x轴上有一点E的横坐标为2a，过点E作y轴的平行线交抛物线于点F，抛物线对称轴与x轴交于点G，Q为抛物线（对称轴的左侧）上一动点，是否存在点Q使GF为 $∠ E F Q$ 的平分线？若存在，求出点Q的坐标；若不存在，请说明理由．

查看试题解析

等级	非常了解	比较了解	基本了解	不太了解
频数	25	55	18	2
频率	0.25	m	0.18	0.02