广东省深圳市坪山区2022年三月份中考模拟数学试题

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图是由4个完全相同的正方形组成的几何体，它的左视图是（）

A、 B、 C、 D、

查看试题解析
2. 若一元二次方程x²+x+a=0有两实数根，则实数a的取值范围是（　　）

A、 $a \geq \frac{1}{4}$ B、 $a > \frac{1}{4}$ C、 $a \leq \frac{1}{4}$ D、 $a < \frac{1}{4}$

查看试题解析
3. 已知点 $P (x_{1} ， - 2)$ ， $Q (x_{2} ， 2)$ ， $R (x_{3} ， 3)$ 三点都在反比例函数 $y = \frac{a^{2} + 1}{x}$ 的图像上，则下列关系正确的是（）．

A、 $x_{1} < x_{2} < x_{3}$ B、 $x_{1} < x_{3} < x_{2}$ C、 $x_{3} < x_{2} < x_{1}$ D、 $x_{2} < x_{3} < x_{1}$

查看试题解析
4. 一元二次方程 $x^{2} + 2 x - 99 = 0$ 变形正确的是（）

A、 $(x + 1)^{2} = 100$ B、 $(x - 1)^{2} = 100$ C、 $(x + 2)^{2} = 100$ D、 $(x - 2)^{2} = 100$

查看试题解析
5. 将抛物线y=x²向左平移两个单位，再向上平移一个单位，可得到抛物线（　　）

A、 $y = (x - 2)^{2} + 1$ B、 $y = (x - 2)^{2} - 1$ C、 $y = (x + 2)^{2} + 1$ D、 $y = (x + 2)^{2} - 1$

查看试题解析
6. 如图，在正六边形桌面中心正上方有一盏吊灯，在灯光下，桌面在水平地面的投影是一个面积为 $\frac{27 \sqrt{3}}{8} m^{2}$ 的正六边形，已知桌子的高度为 $0.75 m$ ，桌面边长为 $1 m$ ，则吊灯距地面的高度为（）

A、 $2.25 m$ B、 $2.3 m$ C、 $2.35 m$ D、 $2.4 m$

查看试题解析
7. 如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=4．点F为射线CB上一动点，过点C作CM⊥AF于M，交AB于E，D是AB的中点，则DM长度的最小值是（　　）

A、 $\sqrt{3}$ B、 $\sqrt{2}$ C、 $1$ D、 $\sqrt{6} - 2$

查看试题解析
8. 有理数 $a ， b ， c$ 在数轴上对应的点的位置如图所示，给出下面的四个命题：
① $a b c < 0$ .② $(a - b) (b - c) (c - a) > 0$ .③ $| a | < 1 - b c$ .④ $| a - b | + | b - c | = | a - c |$ .其中正确的命题有（）个.

A、4 B、3 C、2 D、1

查看试题解析
9. 函数y＝ $\frac{1}{2}$ x²＋1与y＝ $\frac{1}{2}$ x²＋2的图象的不同之处是(　　)

A、对称轴 B、开口方向 C、顶点 D、形状

查看试题解析
10. 如图，在△ABC中，AB＝AC，AD平分∠BAC，DE⊥AB，DF⊥AC，E，F分别为垂足，则下列四个结论：（1）∠DEF＝∠DFE；（2）AE＝AF；（3）AD平分∠EDF；（4）AD垂直平分EF．其中正确的有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析

二、填空题

11. 若菱形的两条对角线分别是方程x²-14x+48=0的两个实数根，则菱形的边长为．

查看试题解析
12. 如图，折叠矩形纸片 $A B C D$ ，使点D落在 $A B$ 边的点M处， $E F$ 为折痕， $A B = 1$ ， $A D = 2$ .设 $A M$ 的长为t，用含有t的式子表示四边形 $C D E F$ 的面积是.

查看试题解析
13. 用抽签的办法从甲，乙，丙，丁四位同学中，任选一位同学去打扫公共场地，选中甲同学的概率是．

查看试题解析
14. 若菱形的面积为24，一条对角线长为6，则其边长长为．

查看试题解析
15. 《九章算术》中，赵爽利用“弦图”（如图①）证明了勾股定理，类比此方法研究等边三角形（如图②）：在等边三角形ABC中，如果∠BAD=∠CBE=∠ACF，那么△ABD的三边存在一定的数量关系，设BD=a，AD=b，AB=c，则这三边a，b，c满足的数量关系是．

查看试题解析

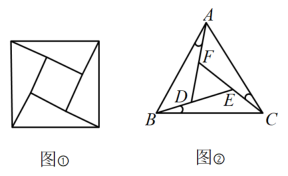
三、解答题

16. 计算： $\sqrt[3]{8}$ -|1- $\sqrt{3}$ |+ $\sqrt{(- 3)^{2}}$

查看试题解析
17. 在平面直角坐标系xOy中，点P的坐标为（a，b），点P的“关联点”P^’的坐标定义如下：当 $a \geq b$ 时，P^’点坐标为（b，a）；当 $a < b$ 时，P^’点坐标为（－a，－b）．

(1)、写出A（5，3）的变换点坐标， B（1，6）的变换点坐标， C（－2，4）的变换点坐标；

(2)、如果直线l： $y = - \frac{1}{2} x + 3$ 上所有点的关联点组成一个新的图形，记作图形W，请画出图形W；

(3)、在（2）的条件下，若直线y=kx－1（k≠0）与图形W有两个交点，请直接写出k的取值范围．

查看试题解析
18. 如图1，某学校开展“交通安全日”活动．在活动中，交警叔叔向同学们展示了大货车盲区的分布情况，并提醒大家：坐在驾驶室的司机根本看不到在盲区中的同学们，所以一定要远离大货车的盲区，保护自身安全．小刚所在的学习小组为了更好的分析大货车盲区的问题，将图1用平面图形进行表示，并标注了测量出的数据，如图2．在图2中大货车的形状为矩形，而盲区1为梯形，盲区2、盲区3为直角三角形，盲区4为正方形．

请你帮助小刚的学习小组解决下面的问题：

(1)、盲区1的面积约是m²；盲区2的面积约是m²；（ $\sqrt{2}$ ≈1.4， $\sqrt{3}$ ≈1.7，sin25°≈0.4，cos25°≈0.9，tan25°≈0.5，结果保留整数）

(2)、如果以大货车的中心A点为圆心，覆盖所有盲区的半径最小的圆为大货车的危险区域，请在图2中画出大货车的危险区域．

查看试题解析
19. 如图，已知 $⊙ O$ ，点 $A$ 在圆上，请以 $A$ 为一顶点作圆内接正方形 $A B C D$ .（保留作图痕迹，不写作法）

查看试题解析
20. 图中所示的抛物线形桥，当找顶离水面4m时，水面宽8m，水面上升3米，水面宽度减少多少?

查看试题解析
21. 在平面直角坐标系中，△ABC的边BC在x轴上，边BC的中点为原点O，点A在y轴上，在线段AB上有一点D（点D不与A、B重合），过点D作AB的垂线，分别交y轴和线段AC于点E和点F，连接DO，若∠AFD=2∠AOD．

(1)、如图1，求∠BDO的度数；

(2)、如图2，延长DF交x轴于点G，若EO=CG，AO=6 $\sqrt{5}$ ，求点E的坐标；

(3)、如图3，在（2）问的条件下，若AD+CF=11，AD：AF=3：5，求BD的长．

查看试题解析
22. 若二次函数y=a₁x²+b₁x+c₁的图象记为C₁ ，其顶点为A，二次函数y=a₂x²+b₂x+c₂的图象记为C₂ ，其顶点为B，且满足点A在C₂上，点B在C₁上，则称这两个二次函数互为“伴侣二次函数”．

(1)、一个二次函数的“伴侣二次函数”有个；

(2)、①求二次函数y=x²+3x+2与x轴的交点；
②求以上述交点为顶点的二次函数y=x²+3x+2的“伴侣二次函数”．

(3)、试探究a₁与a₂满足的数量关系．

查看试题解析