广东省深圳市南山区2022年三月份中考数学模拟试题

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 若一个正方形的面积是28，则它的边长为（　　）

A、 $\sqrt{28}$ B、 $2 \sqrt{7}$ C、 $- 2 \sqrt{7}$ D、 $\sqrt{7}$

查看试题解析
2. 下列事件是必然事件的是（　　）

A、通常温度降到0℃以下，纯净的水结冰 B、随意翻到一本书的某页，这页的页码是奇数 C、汽车累积行驶10000km，从未出现故障 D、购买1张彩票，中奖

查看试题解析
3. 一副直角三角板如图放置，点C在FD的延长线上，AB $∥$ CF，∠F＝∠ACB＝90°，∠A＝60°，∠E＝45°，则∠DBC的度数为（　　）

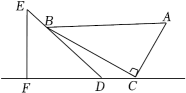A、10° B、15° C、18° D、30°

查看试题解析
4. 一种商品每件成本为80元，原来按成本增加 $30 %$ 定出价格．现由于库存积压，按原价的 $85 %$ 出售，则每件商品的盈亏情况为（）

A、盈利8.4元 B、盈利9.2元 C、亏损8.4元 D、亏损9.2元

查看试题解析
5. 线段AB是直线y＝5x+1的一部分，点A的坐标为（0，1），点B的纵坐标是6，曲线BC是双曲线y $= \frac{k}{x}$ 的一部分，点C的横坐标是6．由点C开始，不断重复曲线“A→B→C”，形成一组波浪线．已知点P（18，m），Q（22，n）均在该组波浪线上，分别过点P，Q向x轴作垂线段，垂足分别为D和E，则四边形PDEQ的面积是（　　）

A、6 B、5 C、9 D、12

查看试题解析
6. 普通火车从绵阳至成都历时大约2小时，成绵城际快车开通后，时间大大缩短至几十分钟，现假定普通火车与城际快车两列对开的火车于同一时刻发车，其中普通火车由成都至绵阳，城际快车由绵阳至成都，这两车在途中相遇之后，各自用了80分钟和20分钟到达自己的终点绵阳、成都，则城际快车的平均速度是普通火车平均速度的（　　）倍．

A、2 B、2.5 C、3 D、4

查看试题解析
7. 勾股定理有着悠久的历史，它曾引起很多人的兴趣.英国佩里加（H.Perigal，1801﹣1898）用“水车翼轮法”（图1）证明了勾股定理.该证法是用线段QX，ST，将正方形BIJC分割成四个全等的四边形，再将这四个四边形和正方形ACYZ拼成大正方形AEFB（图2）.若AD＝ $\sqrt{13}$ ，tan∠AON＝ $\frac{3}{2}$ ，则正方形MNUV的周长为（）

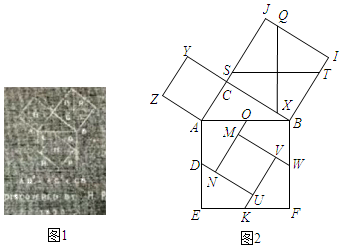A、 $5 \sqrt{13}$ B、18 C、16 D、 $8 \sqrt{3}$

查看试题解析
8. 已知抛物线y＝x²+（2a﹣1）x﹣3，当﹣1≤x≤3时，函数最大值为1，则a值为（　　）

A、 $- \frac{1}{2}$ B、 $- \frac{1}{3}$ C、 $- \frac{1}{2}$ 或 $- \frac{1}{3}$ D、﹣1或 $- \frac{1}{3}$

查看试题解析
9. “数形结合”思想是数学学习的一个重大思想．通过巧妙运用几何代数的结合性有时能将某些难题迎刃而解．已知a，b，c，d均为实数，a²+b²＝c²+d² $= \sqrt{2}$ ，则 $\frac{a^{2} c^{2} + b^{2} d^{2}}{2} +$ abcd的最大值为（　　）

A、 $\sqrt{2}$ B、 $\frac{\sqrt{2}}{2}$ C、1 D、2

查看试题解析
10. 如图，AB是⊙O的直径，AB=10，P是半径OA上的一动点，PC⊥AB交⊙O于点C，在半径OB上取点Q，使得OQ=CP，DQ⊥AB交⊙O于点D，点C，D位于AB两侧，连接CD交AB于点F，点P从点A出发沿AO向终点O运动，在整个运动过程中，△CEP与△DEQ的面积和的变化情况是（　　）

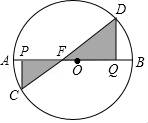A、一直减小 B、一直不变 C、先变大后变小 D、先变小后变大

查看试题解析

二、填空题

11. 已知 $∠ A = 100 °$ ，则 $∠ A$ 的补角等于 $°$ ．

查看试题解析
12. 有五张正面分别标有数字-2，-1，0，1，2的不透明卡片，它们除数字不同外其余全部相同．现将它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为a，将该卡片放回洗匀后从中再任取一张，将该卡片上的数字记为b，则 $a b$ 为非负数的概率为．

查看试题解析
13. 若非零实a，b满足a²＝ab $- \frac{b^{2}}{4}$ ，即可得 $- \frac{b}{a}$ 的值为．

查看试题解析
14.
如图，在半径为5的⊙O中，弦AB=8，P是弦AB所对的优弧上的动点，连接AP，过点A作AP的垂线交射线PB于点C，当△PAB是等腰三角形时，线段BC的长为 .

查看试题解析
15. 如图，在菱形ABCD中，∠BAD＝120°，DE⊥BC交BC的延长线于点E．连结AE交BD于点F，交CD于点G．FH⊥CD于点H，连结CF．则cos∠CFH的值为．

查看试题解析

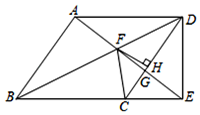
三、解答题

16. 先化简，再求值：（x+1）（x﹣1）+（2﹣x）x，其中 $x = \frac{3 \sqrt{2}}{2}$ ．

查看试题解析
17. 为弘扬中华民族传统文化，某市举办了中小学生“国学经典大赛”，比赛项目为：A．唐诗；B．宋词；C．论语；D．三字经．比赛形式分“单人组”和“双人组”．

(1)、小华参加“单人组”，他从中随机抽取一个比赛项目，恰好抽中“论语”的概率是多少？

(2)、小明和小红组成一个小组参加“双人组”比赛，比赛规则是：同一小组的两名队员的比赛项目不能相同，且每人只能随机抽取一次．则恰好小明抽中“唐诗”且小红抽中“宋词”的概率是多少？小明和小红都没有抽到“三字经”的概率是多少？请用画树状图或列表的方法进行说明．

查看试题解析
18. 如图，某天然气公司的主输气管道途经A小区，继续沿A小区的北偏东60°方向往前铺设，测绘员在A处测得另一个需要安装天然气的M小区位于北偏东30°方向，测绘员从A处出发，沿主输气管道步行到达C处，此时测得M小区位于北偏西60°方向．

(1)、求∠AMC与∠ACM度数．

(2)、现要在主输气管道AC上选择一个支管道连接点N，使从N处到M小区铺设的管道最短，且AC＝2000米，求A小区与支管道连接点N的距离．

查看试题解析
19. 如图，△ABC内接于⊙O（∠ACB＞90°），连接OA，OC．记∠BAC＝α，∠BCO＝β，∠BAO＝γ．

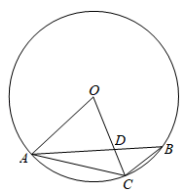(1)、探究α与β之间的数量关系，并证明．

(2)、设OC与AB交于点D，⊙O半径为1，
①若β＝γ+45°，AD＝2OD，求由线段BD，CD，弧BC围成的图形面积S．
②若α+2γ＝90°，设sinα＝k，用含k的代数式表示线段OD的长．

查看试题解析
20. 小李从A地出发去相距4.5千米的B地上班，他每天出发的时间都相同．第一天步行去上班结果迟到了5分钟．第二天骑自行车去上班结果早到10分钟．已知骑自行车的速度是步行速度的1.5倍．

(1)、求小李步行的速度和骑自行车的速度；

(2)、有一天小李骑自行车出发，出发1.5千米后自行车发生故障．小李立即跑步去上班（耽误时间忽略不计）为了至少提前5分钟到达．则跑步的速度至少为多少千米每小时？

查看试题解析
21. 在 $▱ A B C D$ 中， $∠ B A D = α$ ，以点D为圆心，适当的长度为半径画弧，分别交边AD、CD于点M、N，再分别以M、N为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧交于点K，作射线DK，交对角线AC于点G，交射线AB于点E，将线段EB绕点E顺时针旋转 $\frac{1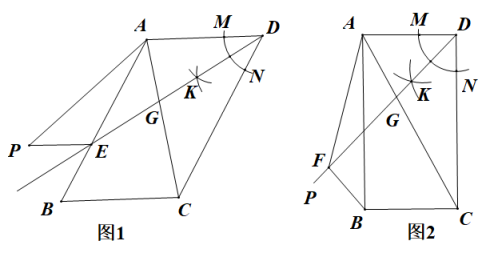}{2} α$ 得线段EP．

(1)、如图1，当 $α = 120 °$ 时，连接AP，线段AP和线段AC的数量关系为；

(2)、如图2，当 $α = 90 °$ 时，过点B作 $B F ⊥ E P$ 于点F，连接AF，请求出∠FAC的度数，以及AF，AB，AD之间的数量关系，并说明理由；

(3)、当 $α = 120 °$ 时，连接AP，若 $B E = \frac{1}{3} A B$ ，请直接写出线段AP与线段DG的比值．

查看试题解析
22. 已知：如图1，在平面直角坐标系中，点A的坐标为（4，0），点B在y轴的正半轴上，且tan∠OAB $= \frac{3}{4}$ ，点P是线段AB上的一个动点，以点P为圆心，PA为半径作⊙P交x轴于C点，记过点A、B、C的抛物线顶点为D点，设PA＝5m．

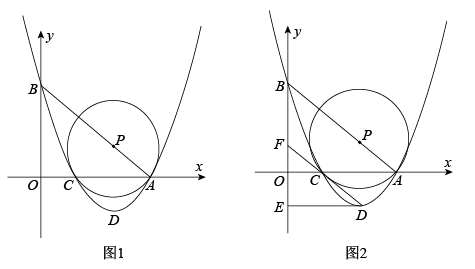(1)、求线段OA和AB的长．

(2)、①求用含字母m的代数式来表示点C的坐标．
②当点C在x轴的正半轴上，且OC：PA＝8：15时，求抛物线的解析式．

(3)、如图2，过点D作DE∥x轴交y轴于点E，作直线CD交y轴于点F，当⊙P与△DEF其中一边所在的直线相切时，求所有满足条件的m的值．

查看试题解析