广东省深圳市龙岗区2022年中考数学一模试题
试卷更新日期:2022-04-26 类型:中考模拟
一、单选题
-
1. 下列四个几何体中,左视图为圆的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一元二次方程 的解是( )A、 B、 C、 D、3. Rt△ABC中∠C=90°,sinA , 则tanA的值是( )A、 B、 C、 D、4. 如图,边长为2的正方形ABCD的对角线相交于点O,过点O的直线分别交边AD、BC于E、F两点,则阴影部分的面积是( )
2. 一元二次方程 的解是( )A、 B、 C、 D、3. Rt△ABC中∠C=90°,sinA , 则tanA的值是( )A、 B、 C、 D、4. 如图,边长为2的正方形ABCD的对角线相交于点O,过点O的直线分别交边AD、BC于E、F两点,则阴影部分的面积是( )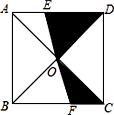 A、1 B、2 C、3 D、45. 某校前年用于绿化的投资为20万元,今年用于绿化的投资为36万元,设这两年用于绿化投资的年平均增长率为x,则列方程得( )A、20(1+2x)=36 B、20(1+x2)=36 C、20(1+x) 2=36 D、20(1+x)+20(1+x) 2=366. 某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
A、1 B、2 C、3 D、45. 某校前年用于绿化的投资为20万元,今年用于绿化的投资为36万元,设这两年用于绿化投资的年平均增长率为x,则列方程得( )A、20(1+2x)=36 B、20(1+x2)=36 C、20(1+x) 2=36 D、20(1+x)+20(1+x) 2=366. 某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
A、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 B、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” C、抛一个质地均匀的正六面体骰子,向上的面点数是5 D、抛一枚硬币,出现反面的概率7. 如图,在平面直角坐标系中,已知 , , , ABC与DEF位似,原点O是位似中心,则E点的坐标是( ) A、 B、 C、 D、8. 下列命题中,假命题的是( ).A、顺次连接对角线相等的四边形的四边中点所形成的图形是菱形; B、各边对应成比例的两个多边形相似; C、反比例函数的图象既是轴对轴图形,也是中心对称图形; D、已知二次函数 , 当时,y随x的增大而减小.9. 如图,A,B两点的坐标分别是 , , 抛物线的顶点在线段AB上运动,与x轴交于C,D两点(C在D的左侧),点C的最小值为-1,则D点的横坐标的最大值是( )
A、 B、 C、 D、8. 下列命题中,假命题的是( ).A、顺次连接对角线相等的四边形的四边中点所形成的图形是菱形; B、各边对应成比例的两个多边形相似; C、反比例函数的图象既是轴对轴图形,也是中心对称图形; D、已知二次函数 , 当时,y随x的增大而减小.9. 如图,A,B两点的坐标分别是 , , 抛物线的顶点在线段AB上运动,与x轴交于C,D两点(C在D的左侧),点C的最小值为-1,则D点的横坐标的最大值是( ) A、1 B、3 C、5 D、610. 如图,在菱形ABCD中,对角线AC与BD相交于点O,在BC的延长线上取一点E,连接OE交CD于点F.已知 , , 则CF的长是( )
A、1 B、3 C、5 D、610. 如图,在菱形ABCD中,对角线AC与BD相交于点O,在BC的延长线上取一点E,连接OE交CD于点F.已知 , , 则CF的长是( )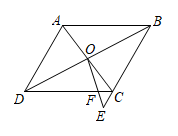 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 四条线段a、b、c、d成比例,其中cm、cm、cm,则线段cm.12. 已知关于x的一元二次方程有两个相等的实数根,则k= .13. 小明的身高为1.6m,某一时刻他在阳光下的影子长为2m,与他邻近的一棵树的影长为10m,则这棵树的高为m.14. 如图,A,B两点分别在x轴正半轴,y轴正半轴上且 , , 将△AOB沿AB翻折得ADB,反比例函数的图像恰好经过D点,则k的值是 .
 15. 如图,在正方形ABCD中,M是对角线BD上一点,连接AM,将AM绕点A逆时针旋转90°得AN,连接MN交AD于E点,连接DN.则下列结论中:①;②;③;④当时,则 . 其中正确结论的序号是 .
15. 如图,在正方形ABCD中,M是对角线BD上一点,连接AM,将AM绕点A逆时针旋转90°得AN,连接MN交AD于E点,连接DN.则下列结论中:①;②;③;④当时,则 . 其中正确结论的序号是 .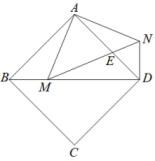
三、解答题
-
16. 计算:17. 为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.(1)、小明从中随机抽取一张卡片是足球社团B的概率是 .(2)、小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率.18. 如图,上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,9时30分到达B处,从A,B两处分别测得小岛C在北偏东45°和北偏东15°.
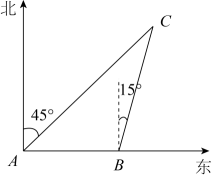 (1)、求∠C的度数;(2)、求B处船与小岛C的距离(结果保留根号).19. 如图,等腰ABC中, , 交BC于D点,E点是AB的中点,分别过D,E两点作线段AC的垂线,垂足分别为G,F两点.
(1)、求∠C的度数;(2)、求B处船与小岛C的距离(结果保留根号).19. 如图,等腰ABC中, , 交BC于D点,E点是AB的中点,分别过D,E两点作线段AC的垂线,垂足分别为G,F两点. (1)、求证:四边形DEFG为矩形;(2)、若 , , 求CG的长.20. 某水果超市以每千克20元的价格购进一批樱桃,规定每千克樱桃售价不低于进价又不高于40元,经市场调查发现,樱桃的日销售量y(千克)与每千克售价x(元)满足一次函数关系 ,(1)、该超市要想获得1000元的日销售利润,每千克樱桃的售价应定为多少元?(2)、当每千克樱桃的售价定为多少元时,日销售利润最大?最大利润是多少?21. 如图1,直线的图像与x轴、y轴分别交于A、B两点,点D是线段AB上一点,过D点分别作OA、OB的垂线,垂足分别是C、E,矩形OCDE的面积为4,且 .
(1)、求证:四边形DEFG为矩形;(2)、若 , , 求CG的长.20. 某水果超市以每千克20元的价格购进一批樱桃,规定每千克樱桃售价不低于进价又不高于40元,经市场调查发现,樱桃的日销售量y(千克)与每千克售价x(元)满足一次函数关系 ,(1)、该超市要想获得1000元的日销售利润,每千克樱桃的售价应定为多少元?(2)、当每千克樱桃的售价定为多少元时,日销售利润最大?最大利润是多少?21. 如图1,直线的图像与x轴、y轴分别交于A、B两点,点D是线段AB上一点,过D点分别作OA、OB的垂线,垂足分别是C、E,矩形OCDE的面积为4,且 . (1)、求D点坐标;(2)、将矩形OCDE以1个单位/秒的速度向右平移,平移后记为矩形MNPQ,记平移时间为t秒.
(1)、求D点坐标;(2)、将矩形OCDE以1个单位/秒的速度向右平移,平移后记为矩形MNPQ,记平移时间为t秒.①如图2,当矩形MNPQ的面积被直线AB平分时,求t的值;
②如图3,当矩形MNPQ的边与反比例函数的图像有两个交点,记为T、K,若直线TK把矩形面积分成1:7两部分,请直接写出t的值.
22. 如图1,已知,抛物线经过、、三点,点P是抛物线上一点. (1)、求抛物线的解析式;(2)、当点P位于第四象限时,连接AC,BC,PC,若 , 求直线PC的解析式;(3)、如图2,当点P位于第二象限时,过P点作直线AP,BP分别交y轴于E,F两点,请问的值是否为定值?若是,请求出此定值;若不是,请说明理由.
(1)、求抛物线的解析式;(2)、当点P位于第四象限时,连接AC,BC,PC,若 , 求直线PC的解析式;(3)、如图2,当点P位于第二象限时,过P点作直线AP,BP分别交y轴于E,F两点,请问的值是否为定值?若是,请求出此定值;若不是,请说明理由.