广东省清远市英德市2022年中考一模数学试题
试卷更新日期:2022-04-26 类型:中考模拟
一、单选题
-
1. -7的相反数是( )A、 B、 C、 D、2. 一个数用科学记数法表示为3.14×105 , 则这个数是( )A、314 B、3140 C、31400 D、3140003. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图所示的几何体的俯视图是( )
4. 如图所示的几何体的俯视图是( )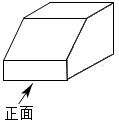 A、
A、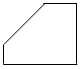 B、
B、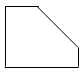 C、
C、 D、
D、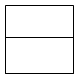 5. 某班6名同学在一次“1分钟仰卧起坐”测试中,成绩分别为(单位:次):38,45,41,37,40,38.这组数据的众数、中位数分别是( )A、45,40 B、38,39 C、38,38 D、45,386. 下列运算结果为的是( )A、 B、a4-a C、 D、7. 如图, , 点O在直线l1上,且∠AOB=90°,若∠2=51°,则∠1的度数为( )
5. 某班6名同学在一次“1分钟仰卧起坐”测试中,成绩分别为(单位:次):38,45,41,37,40,38.这组数据的众数、中位数分别是( )A、45,40 B、38,39 C、38,38 D、45,386. 下列运算结果为的是( )A、 B、a4-a C、 D、7. 如图, , 点O在直线l1上,且∠AOB=90°,若∠2=51°,则∠1的度数为( )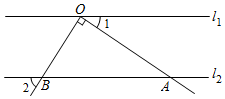 A、51° B、49° C、39° D、29°8. 不等式组 解集在数轴上表示正确的是( )A、
A、51° B、49° C、39° D、29°8. 不等式组 解集在数轴上表示正确的是( )A、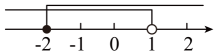 B、
B、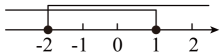 C、
C、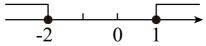 D、
D、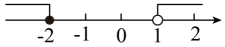 9. 如图,在平面直角坐标系中,与位似,点O是它们的位似中心,已知 , , 则与的面积之比为( )
9. 如图,在平面直角坐标系中,与位似,点O是它们的位似中心,已知 , , 则与的面积之比为( )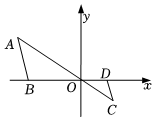 A、 B、 C、 D、10. 如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2 , 运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
A、 B、 C、 D、10. 如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2 , 运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )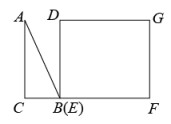 A、
A、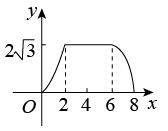 B、
B、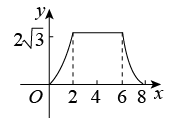 C、
C、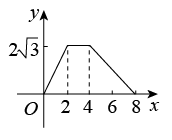 D、
D、
二、填空题
-
11. 因式分解:4m2﹣16= .12. 一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .13. 2022北京冬奥会延庆赛区正在筹建的高山滑雪速滑雪道的平均坡角约为 , 在此雪道向下滑行100米,高度大约下降了米.14. 某市林业部门要考察某种幼树在一定条件下的移植成活率,实验结果统计如下:
移植总数(n)
50
270
400
750
1500
3500
7000
9000
14000
成活数(m)
47
235
369
662
1335
3180
6321
8073
12628
成活频率()
0.94
0.87
0.923
0.883
0.89
0.908
0.903
0.897
0.902
由此可以估计该种幼树移植成活的概率为 . (结果保留小数点后两位)
15. 关于x的一元二次方程x2+2x+m=0有一根为2,则m的值为 .16. 若a﹣2b﹣1=0,则代数式2a﹣4b的值为.17. 学校花园边墙上有一宽为的矩形门 , 量得门框对角线长为 , 为美化校园,现准备打掉地面上方的部分墙体,使其变为以为直径的圆弧形门,则要打掉墙体(阴影部分)的面积是 .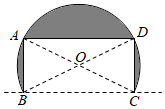
三、解答题
-
18. 计算: .19. 下面是“作一个角等于已知角”的尺规作图过程.已知:∠AOB,求作:一个角,使它等于∠AOB.作法:如图
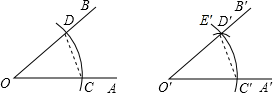
①作射线 ;
②以O为圆心,任意长为半径作孤,交OA于C,交OB于D;
③以 为圆心,OC为半径作弧 ,交 于 ;
④以 为圆心,CD为半径作弧,交弧 于 ;
⑤过点 作射线 ,则 就是所求作的角
请完成下列问题:
(1)、该作图的依据是(填序号)①ASA;②SAS;③AAS;④SSS(2)、请证明 =∠AOB20. 为了解某校学生的课余兴趣爱好情况,某调查小组设计了“阅读”、“打球”、“书法”和“舞蹈”四个选项,用随机抽样的方法调查了该校部分学生的课余兴趣爱好情况(每个学生必须选一项且只能选一项),并根据调查结果绘制了如图统计图: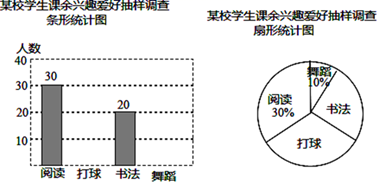
根据统计图所提供的信息,解答下列问题:
(1)、本次抽样调查中的学生人数是;(2)、补全条形统计图;(3)、若该校共有1000名学生,请根据统计结果估计该校课余兴趣爱好为“打球”的学生人数.21. 如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使得CF=BE,连接DF,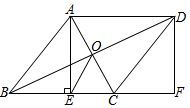 (1)、求证:四边形AEFD是矩形;(2)、连接OE,若AB=13,OE=2 , 求AE的长.22. 2020年我国新型冠状病毒肺炎疫情防控工作进入常态化,某社区为检测出入小区人员体温情况,特采购了一批测温枪,已知1支A型号测温枪和2支B型号测温枪共需380元,2支A型号测温枪和3支B型号测温枪共需610元.(1)、两种型号的测温枪的单价各是多少元?(2)、已知该社区需要采购两种型号的测温枪共40支,且A型号的数量不超过B型号的数量的3倍,请设计出最省钱的购买方案,并说明理由.23. 如图,一次函数(为常数,且)的图象与反比例函数(为常数,且)的图象相交于 , 两点.
(1)、求证:四边形AEFD是矩形;(2)、连接OE,若AB=13,OE=2 , 求AE的长.22. 2020年我国新型冠状病毒肺炎疫情防控工作进入常态化,某社区为检测出入小区人员体温情况,特采购了一批测温枪,已知1支A型号测温枪和2支B型号测温枪共需380元,2支A型号测温枪和3支B型号测温枪共需610元.(1)、两种型号的测温枪的单价各是多少元?(2)、已知该社区需要采购两种型号的测温枪共40支,且A型号的数量不超过B型号的数量的3倍,请设计出最省钱的购买方案,并说明理由.23. 如图,一次函数(为常数,且)的图象与反比例函数(为常数,且)的图象相交于 , 两点.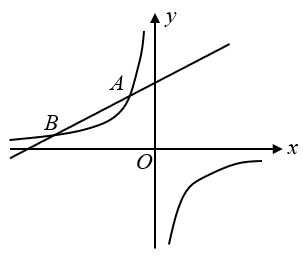 (1)、求n的值;(2)、若一次函数的图象与反比例函数的图象有且只有一个公共点,求m的值.
(1)、求n的值;(2)、若一次函数的图象与反比例函数的图象有且只有一个公共点,求m的值.