安徽省芜湖市2022年九年级毕业暨升学模拟考试（一）数学试题

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 天气预报称，明天芜湖市全市的降水率为 $90 %$ ，下列理解正确的是（）．

A、明天芜湖市全市下雨的可能性较大 B、明天芜湖市全市有 $90 %$ 的地方会下雨 C、明天芜湖市全天有 $90 %$ 的时间会下雨 D、明天芜湖市一定会下雨

查看试题解析
2. 下列函数中，图象经过原点的是（）

A、 $y = 1 - 3 x$ B、 $y = 2 x$ C、 $y = \frac{4}{x}$ D、 $y = x^{2} - 1$

查看试题解析
3. 若关于x的一元二次方程（m+1）x²+3x+m²﹣1＝0的一个实数根为0，则m等于（）

A、1 B、±1 C、﹣1 D、0

查看试题解析
4. 将抛物线C₁：y＝（x－3）²＋2向左平移3个单位长度，得到抛物线C₂ ，抛物线C₂与抛物线C₃关于x轴对称，则抛物线C₃的解析式为（　　　）．

A、y＝x²－2 B、y＝－x²＋2 C、y＝x²＋2 D、y＝－x²－2

查看试题解析
5. 如图所示，将△ABC绕顶点C顺时针旋转35°得到△DEC，点A、B的对应点分别是点D和点E．设边ED，AC相交于点F．若∠A＝30°，则∠EFC的度数为（）．

A、60° B、65° C、72.5° D、115°

查看试题解析
6. 如图，点D、E分别在△ABC的AB、AC边上，下列条件中：①∠ADE＝∠C；② $\frac{A E}{A B} = \frac{D E}{B C}$ ；③ $\frac{A D}{A C} = \frac{A E}{A B}$ ．使△ADE与△ACB一定相似的是（）

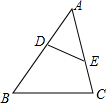A、①② B、②③ C、①③ D、①②③

查看试题解析
7. 已知△ABC的三边长分别为6 cm，7.5 cm，9 cm，△DEF的一边长为4 cm，若想得到这两个三角形相似，则△DEF的另两边长是下列的（）

A、2 cm，3 cm B、4 cm，5 cm C、5 cm，6 cm D、6 cm，7 cm

查看试题解析
8. 已知实数 $x$ 满足 ${(x^{2} - x)}^{2} - 4 (x^{2} - x) - 12 = 0$ ，则代数式 $x^{2} - x + 1$ 的值是（）

A、7 B、-1 C、7或-1 D、-5或3

查看试题解析
9. 已知⊙O的直径CD=10cm，AB是⊙O的弦，AB=8cm，且AB⊥CD，垂足为M，则AC的长为（）

A、2 $\sqrt{5}$ cm B、4 $\sqrt{5}$ cm C、2 $\sqrt{5}$ cm或4 $\sqrt{5}$ cm D、2 $\sqrt{3}$ cm或4 $\sqrt{3}$ cm

查看试题解析
10. 如图，菱形ABCD的对角线AC，BD相交于点O，AC＝6，BD＝8，动点P从点B出发，沿着B﹣A﹣D在菱形ABCD的边上运动，运动到点D停止，点P′是点P关于BD的对称点，PP′交BD于点M，若BM＝x，△OPP′的面积为y，则y与x之间的函数图象大致为（　　）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 点A（﹣1，1）关于原点对称的点的坐标是．

查看试题解析
12. 为推进“书香芜湖”建设，让市民在家门口即可享受阅读和休闲服务，某社区开办了社区书屋.2021年9月份书屋共接待了周边居民200人次，11月份共接待了648人次，假定9月至11月每月接待人次增长率相同设为x，则可列方程．

查看试题解析
13. 如图所示，⊙O中弦AD与BC交于点E，连接AB、CD，若 $\frac{A B}{C D} = \frac{\sqrt{2}}{\sqrt{3}}$ ，则△ABE与△CDE的面积比为．

查看试题解析
14. 如图所示，在平面直角坐标系中，点A的坐标为（4，0），点P为y轴上一点，且满足条件PQ⊥AP，∠QAP＝30°．

(1)、当OP＝ $\sqrt{3}$ 时，OQ＝；

(2)、若点P在y轴上运动，则OQ的最小值为．

查看试题解析

三、解答题

15. 解方程： $x (x - 3) + x - 3 = 0$

查看试题解析
16. 如图所示的网格图中，每个小正方形边长均为1，点O和△ABC的顶点均为小正方形的顶点．

(1)、以O为位似中心，在网格图中作 $△ A^{'} B^{'} C^{'}$ ，使 $△ A^{'} B^{'} C^{'}$ 和 $△ A B C$ 位似，且位似比为1∶2；

(2)、连结（1）中的点A和点 $A^{'}$ ，则四边形 $A A^{'} C^{'} C$ 的周长为．（结果保留根号）

查看试题解析
17. 《九章算术》中记载了一种测量井深的方法．如图所示，在井口B处立一根垂直于井口的木杆BD，从木杆的顶端D点观察井内水岸C点，视线DC与井口的直径AB交于点E．如果测得AB＝1.8米，BD＝1米，BE＝0.2米．请求出井深AC的长．

查看试题解析
18. 已知二次函数y＝x²－2x＋a过点（2，2）．

(1)、求二次函数解析式及图象的对称轴；

(2)、当n≤x≤2时（n为常数），对应的函数值y的取值范围是1≤y≤10，试求n的值．

查看试题解析
19. 如图1，BC是⊙O的直径，点A，P为其异侧的两点（点A、P均不与点B、C重合），过点A作AQ⊥AP，交PC的延长线于点Q，连接AQ交⊙O于点D．

(1)、求证：△APQ∽△ABC．

(2)、如图2，若AB＝3，AC＝4.当点C为弧PD的中点时，求CQ的长．

查看试题解析
20. 已知：反比例函数 $y_{1} = \frac{4}{x} (x > 0)$ 的图象与一次函数 $y_{2} = \frac{1}{2} x + 1$ （x≥0）的图象交于点A．

(1)、在同一个平面直角坐标系中，请画出函数y₁与函数 $y_{2}$ 的图象；并观察图象，直接写出不等式 $\frac{4}{x}$ ≤ $\frac{1}{2} x + 1$ 在第一象限成立时x的取值范围；

(2)、已知点P（n，0）（n＞0），过点P作垂直于x轴的直线，与反比例函数图象交于点B，与直线交于点C．记反比例函数图象在点A，B之间的部分与线段AC，BC围成的区域（不含边界）为W．
①当n＝5时，区域W内的格点个数为；（格点即横、纵坐标都是整数的点）
②若区域W内的格点恰好为2个，请结合函数图象，直接写出n的取值范围．

查看试题解析
21. 邮票素有“国家名片”之称，方寸之间，包罗万象．为宣传2022年北京冬奥会，中国邮政发行了一套冬奥会邮票，其中有一组展现雪上运动的邮票，如图所示：
某班级举行冬奥会有奖问答活动，答对的同学可以随机抽取邮票作为奖品．

(1)、在抢答环节中，若答对一题，可从4枚邮票中任意抽取1枚作为奖品，则恰好抽到“冬季两项”的概率是；

(2)、在抢答环节中，若答对两题，则可从4枚邮票中任意抽取2枚作为奖品，求恰好抽到“高山滑雪”和“自由式滑雪”的概率．

查看试题解析
22. 如图1所示的某种发石车是古代一种远程攻击的武器，发射出去的石块的运动轨迹是抛物线的一部分，且距离发射点20米时达到最大高度10米．将发石车置于山坡底部O处，山坡上有一点A，点A与点O的水平距离为30米，与地面的竖直距离为3米，AB是高度为3米的防御墙．若以点O为原点，建立如图2所示的平面直角坐标系．

(1)、求石块运动轨迹所在抛物线的解析式；

(2)、试通过计算说明石块能否飞越防御墙AB；

(3)、在竖直方向上，试求石块飞行时与坡面OA的最大距离．

查看试题解析
23. 如图，在正方形ABCD中，P是边BC上的一个动点（不与点B，C重合），作点B关于直线AP的对称点E，连接AE，再连接DE并延长交射线AP于点F，连接BF和CF．

(1)、若∠BAP＝ $α$ ，则∠AED＝（用含 $α$ 的式子直接填空）；

(2)、求证：点F在正方形ABCD的外接圆上；

(3)、求证：AF﹣CF＝ $\sqrt{2}$ BF．

查看试题解析