安徽省马鞍山市和县2022年中考第一次模拟监测数学试题
试卷更新日期:2022-04-26 类型:中考模拟
一、单选题
-
1. 在四个数0,-2,-3,2中,最小的数是( )A、0 B、-2 C、-3 D、22. 下列计算正确的是( )A、 B、 C、 D、3. 北京冬奥会和冬残奥会赛会志愿者招募工作进展顺利,截止 年底,赛会志愿者申请人数已突破 人.将 用科学记数法表示为( )A、 B、 C、 D、4. 下列几何体中,主视图是圆的是( )A、
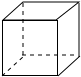 B、
B、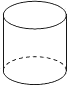 C、
C、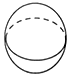 D、
D、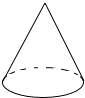 5. 化简 的结果是( )A、 +1 B、 C、 D、6. 不等式组的解集是( )A、﹣1<x≤2 B、﹣2≤x<1 C、x<﹣1或x≥2 D、2≤x<﹣17. 如图, , , 则的值是( )
5. 化简 的结果是( )A、 +1 B、 C、 D、6. 不等式组的解集是( )A、﹣1<x≤2 B、﹣2≤x<1 C、x<﹣1或x≥2 D、2≤x<﹣17. 如图, , , 则的值是( ) A、 B、 C、 D、8. 如图,在平面直角坐标系中,轴于点E,正比例函数的图象和反比例函数的图象相交于两点,则点B的坐标是( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,轴于点E,正比例函数的图象和反比例函数的图象相交于两点,则点B的坐标是( ) A、 B、 C、 D、9. 如图,菱形的边长为2, , 动点P从点B出发,沿的路线向点D运动.设的面积为y(B、P两点重合时,的面积可以看作0),点P运动的路程为x,则y与x之间函数关系的图象大致为( )
A、 B、 C、 D、9. 如图,菱形的边长为2, , 动点P从点B出发,沿的路线向点D运动.设的面积为y(B、P两点重合时,的面积可以看作0),点P运动的路程为x,则y与x之间函数关系的图象大致为( )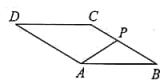 A、
A、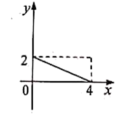 B、
B、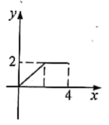 C、
C、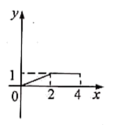 D、
D、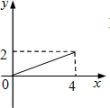 10. 如图,在 中, ,点 是 边上一动点,过点 作 交 的延长线于 .若 , ,则 的最小值为( )
10. 如图,在 中, ,点 是 边上一动点,过点 作 交 的延长线于 .若 , ,则 的最小值为( ) A、 B、1 C、 D、
A、 B、1 C、 D、二、填空题
-
11. 若 , 且m,n为两个连续的整数,则的值为 .12. 因式分解: .13. 为了在校运会中取得更好的成绩,小丁积极训练,在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是1.68米,当铅球运行的水平距离为2米时,达到最大高度2米的B处,则小丁此次投掷的成绩是米.
 14. 如图,点Q是△ABC内一点,且满足∠QAB=∠QBC=∠QCA=∠a.
14. 如图,点Q是△ABC内一点,且满足∠QAB=∠QBC=∠QCA=∠a.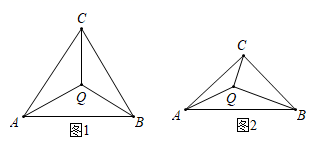 (1)、如图1,当△ABC是等边三角形时,∠a= .(2)、如图2,当△ABC 是等腰直角三角形(其中 ∠ACB=90°)时,△QAC、△QBA、△QCB的面积之比是 .
(1)、如图1,当△ABC是等边三角形时,∠a= .(2)、如图2,当△ABC 是等腰直角三角形(其中 ∠ACB=90°)时,△QAC、△QBA、△QCB的面积之比是 .三、解答题
-
15. 计算: .16. 我国北魏数学家张丘建的著作《张丘建算经》对于不定方程的典型问题有独到见解,其中记载了这样一个问题,原文是:“今甲乙怀银,不知其数,乙得甲十银,适等,甲得乙十银,多乙余钱五倍,问甲乙各怀银几何?”译文为:现有甲、乙两人,带有一些银子,都不知道数量,甲给乙的10两银子,两人的银子恰好相等;乙给甲的10两银子,甲比乙多出的银子是乙的5倍,问甲、乙各带了多少两银子?请解答上述问题.17. 如图,的顶点坐标分别为 , , .

( 1 )画出绕点C顺时针旋转90°得到的 , 并写出的坐标;
( 2 )以点O为位似中心,将放大为原来的2倍,得到 , 请在网格中画出 .
18. 观察以下等式:第1个等式:
第 个等式:
第3个等式:
第 个等式:
第5个等式:
······
按照以上规律.解决下列问题:
(1)、写出第6个等式;(2)、写出你猜想的第n个等式:(用含n的等式表示),并证明.19. 如图,斜立于地面的木杆AB,从点C处折断后,上半部分BC倒在地上,杆的顶部B恰好接触到地面D处,测得∠ACD=60°,∠ADC=37°,杆的底部A与点D相距5米,求木杆AB的长度.(精确到0.1米;参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,≈1.73) 20. 如图, 为 的直径, 是 上的一点,连接 , . 是 的中点,过 作 于点 ,交 于点 .
20. 如图, 为 的直径, 是 上的一点,连接 , . 是 的中点,过 作 于点 ,交 于点 . (1)、求证: ;(2)、若 , ,求 的长.21. 某校体育组为了解全校学生“最喜欢的一项球类项目”,随机抽取了部分学生进行调查,下面是根据调查结果绘制的不完整的统计图.请你根据统计图回答下列问题:
(1)、求证: ;(2)、若 , ,求 的长.21. 某校体育组为了解全校学生“最喜欢的一项球类项目”,随机抽取了部分学生进行调查,下面是根据调查结果绘制的不完整的统计图.请你根据统计图回答下列问题: (1)、本次调查的学生共有人,扇形统计图中喜欢乒乓球的学生所占的百分比为;(2)、请补全条形统计图(图2),并估计全校500名学生中最喜欢“足球”项目的有多少人?(3)、篮球教练在制定训练计划前,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈,请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.22. 在平面直角坐标系中,点O为坐标原点,设抛物线的顶点为A.直线与抛物线交于A,B两点 .(1)、求k,b的值;(2)、若点P在线段上任意一点,过P作x轴的垂线,垂足为C,的延长线交抛物线于点D,求线段的最大值.23. 已知:△ABC和△ADE按如图所示方式放置,点D在△ABC内,连接BD、CD和CE,且∠DCE=90°.
(1)、本次调查的学生共有人,扇形统计图中喜欢乒乓球的学生所占的百分比为;(2)、请补全条形统计图(图2),并估计全校500名学生中最喜欢“足球”项目的有多少人?(3)、篮球教练在制定训练计划前,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈,请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.22. 在平面直角坐标系中,点O为坐标原点,设抛物线的顶点为A.直线与抛物线交于A,B两点 .(1)、求k,b的值;(2)、若点P在线段上任意一点,过P作x轴的垂线,垂足为C,的延长线交抛物线于点D,求线段的最大值.23. 已知:△ABC和△ADE按如图所示方式放置,点D在△ABC内,连接BD、CD和CE,且∠DCE=90°. (1)、如图①,当△ABC和△ADE均为等边三角形时,试确定AD、BD、CD三条线段的关系,并说明理由;(2)、如图②,当BA=BC=2AC,DA=DE=2AE时,试确定AD、BD、CD三条线段的关系,并说明理由;(3)、如图③,当AB:BC:AC=AD:DE:AE=m:n:p时,请直接写出AD、BD、CD三条线段的关系.
(1)、如图①,当△ABC和△ADE均为等边三角形时,试确定AD、BD、CD三条线段的关系,并说明理由;(2)、如图②,当BA=BC=2AC,DA=DE=2AE时,试确定AD、BD、CD三条线段的关系,并说明理由;(3)、如图③,当AB:BC:AC=AD:DE:AE=m:n:p时,请直接写出AD、BD、CD三条线段的关系.