安徽省怀宁县2022年九年级下学期学情调研数学试题
试卷更新日期:2022-04-26 类型:中考模拟
一、单选题
-
1. 比﹣3小的数是( )A、0 B、1 C、﹣2 D、﹣52. 已知⊙O的直径是4cm,OP=4cm,则点P( )A、在⊙O外 B、在⊙O上 C、在⊙O内 D、不能确定3. 据新华社消息,2022北京冬奥会开幕式中国大陆地区观看人数约为3.16亿人,其中3.16亿用科学记数法表示为( ).A、3.16×107 B、3.16×108 C、3.16×109 D、3.16×10104. 下列几何体的主视图、左视图、俯视图都相同的是( )A、
 B、
B、 C、
C、 D、
D、 5. 一个布袋里装有3个只有颜色不同的球,其中2个红球,1个白球.从布袋里摸出一个球,记下颜色后放回,搅匀,再摸出一个球,则两次摸到的球都是红球的概率是( )A、 B、 C、 D、6. 设a,b是方程 的两个实数根,则 的值为( )A、2020 B、2021 C、2022 D、20237. 小明和他的爸爸妈妈共3人站成一排拍照,他的爸爸妈妈相邻的概率是( )A、 B、 C、 D、8. 如图, 与 相交于点 ,点 在线段 上,且 .若 , , ,则 的值为( )
5. 一个布袋里装有3个只有颜色不同的球,其中2个红球,1个白球.从布袋里摸出一个球,记下颜色后放回,搅匀,再摸出一个球,则两次摸到的球都是红球的概率是( )A、 B、 C、 D、6. 设a,b是方程 的两个实数根,则 的值为( )A、2020 B、2021 C、2022 D、20237. 小明和他的爸爸妈妈共3人站成一排拍照,他的爸爸妈妈相邻的概率是( )A、 B、 C、 D、8. 如图, 与 相交于点 ,点 在线段 上,且 .若 , , ,则 的值为( ) A、 B、 C、 D、9. 如图,⊙O是△ABC的外接圆, , 于点P, , 则⊙O的直径为( ).
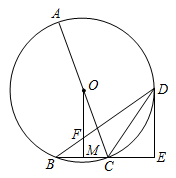
A、 B、 C、 D、9. 如图,⊙O是△ABC的外接圆, , 于点P, , 则⊙O的直径为( ).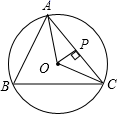 A、 B、 C、6 D、1210. 如图,AB是半圆O的直径,四边形CDMN和DEFG都是正方形,其中点C,D,E在AB上,点F,N在半圆上.若半圆O的半径为10,则正方形CDMN的面积与正方形DEFG的面积之和是( )
A、 B、 C、6 D、1210. 如图,AB是半圆O的直径,四边形CDMN和DEFG都是正方形,其中点C,D,E在AB上,点F,N在半圆上.若半圆O的半径为10,则正方形CDMN的面积与正方形DEFG的面积之和是( ) A、25 B、50 C、100 D、150
A、25 B、50 C、100 D、150二、填空题
-
11. 因式分解:12. 如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为40,则△BEF的面积=
 13. 如图,在直角坐标系中,第一象限内的点A,B都在反比例函数的图象上,横坐标分别是4和2,点C在x轴的正半轴上,满足 . 且 , 则k的值是
13. 如图,在直角坐标系中,第一象限内的点A,B都在反比例函数的图象上,横坐标分别是4和2,点C在x轴的正半轴上,满足 . 且 , 则k的值是 14. 如图,在Rt△ABC中,∠CAB=90°,I为△ABC的内心,延长CI交AB于点D.
14. 如图,在Rt△ABC中,∠CAB=90°,I为△ABC的内心,延长CI交AB于点D.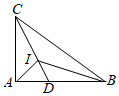 (1)、∠BIC=°;(2)、若BD=3,BI=4,则AB= .
(1)、∠BIC=°;(2)、若BD=3,BI=4,则AB= .三、解答题
-
15. 解不等式组:16. 已知二次函数图象过点A(2,1),B(4,1)且最大值为2,求二次函数的解析式.17. 我国海域辽阔,渔业资源丰富,如图,现有渔船以18km/h的速度在南海海面上沿正东方向航行,当行至A处时,发现它的东南方向有一灯塔B,船续向东航行1h后达到C处,发现灯塔B在它的南偏东15°方向,求此时渔船与灯塔B的距离.
 18. 如图,正方形的边长为4,以点A为圆心,为半径画圆弧得到扇形(阴影部分,点E在对角线上).若扇形正好是一个圆锥的侧面展开图,求圆锥的底面圆的半径.
18. 如图,正方形的边长为4,以点A为圆心,为半径画圆弧得到扇形(阴影部分,点E在对角线上).若扇形正好是一个圆锥的侧面展开图,求圆锥的底面圆的半径. 19. 如图,在平面直角坐标系中,以点M(3,5)为圆心,AB为直径的圆与x轴相切,与y轴交于A,C两点,求点B的坐标.
19. 如图,在平面直角坐标系中,以点M(3,5)为圆心,AB为直径的圆与x轴相切,与y轴交于A,C两点,求点B的坐标.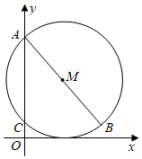 20. 抛物线y=x2﹣3x﹣4与x轴交于点A,点B,与y轴交于点C,直线y=kx+b,经过点B,C.
20. 抛物线y=x2﹣3x﹣4与x轴交于点A,点B,与y轴交于点C,直线y=kx+b,经过点B,C. (1)、点P是直线BC下方抛物线上一动点,求四边形ACPB面积最大时点P的坐标;(2)、若M是抛物线上一点,且∠MCB=15°,请直接写出点M的坐标.21. 2022北京冬奥会,为了解学生最喜欢的冰雪运动,学校从全校随机抽取了部分学生,进行了问卷调查(每个被调查的学生在4种冰雪运动中只选择最喜欢做的一种),4种冰雪运动分别是:A、滑雪,B、滑冰,C、冰球,D、冰壶;将数据进行整理并绘制成如图两幅统计图(未画完整).
(1)、点P是直线BC下方抛物线上一动点,求四边形ACPB面积最大时点P的坐标;(2)、若M是抛物线上一点,且∠MCB=15°,请直接写出点M的坐标.21. 2022北京冬奥会,为了解学生最喜欢的冰雪运动,学校从全校随机抽取了部分学生,进行了问卷调查(每个被调查的学生在4种冰雪运动中只选择最喜欢做的一种),4种冰雪运动分别是:A、滑雪,B、滑冰,C、冰球,D、冰壶;将数据进行整理并绘制成如图两幅统计图(未画完整).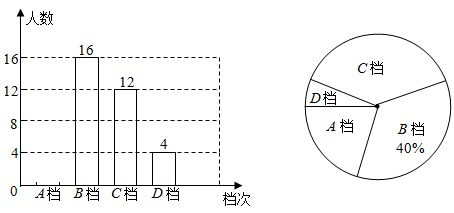 (1)、这次调查中,一共调查了 名学生,请补全条形统计图;(2)、若全校有2800名学生,请估计该校最喜欢“滑冰”运动项目的学生数;(3)、学校想要从D档的4名学生中随机抽取2名同学谈谈自己的喜爱的原因,已知这4名学生中1名来自七年级,1名来自八年级,2名来自九年级,请用列表或画树状图的方法,求抽到的2名学生来自不同年级的概率.
(1)、这次调查中,一共调查了 名学生,请补全条形统计图;(2)、若全校有2800名学生,请估计该校最喜欢“滑冰”运动项目的学生数;(3)、学校想要从D档的4名学生中随机抽取2名同学谈谈自己的喜爱的原因,已知这4名学生中1名来自七年级,1名来自八年级,2名来自九年级,请用列表或画树状图的方法,求抽到的2名学生来自不同年级的概率.