安徽省合肥市庐阳区2022年一模数学试题
试卷更新日期:2022-04-26 类型:中考模拟
一、单选题
-
1. 2022的倒数是( )A、-2022 B、2020 C、 D、2. 计算的结果是( )A、 B、 C、 D、3. 国家卫健委每日都会公布全国31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗剂次.至2021年12月15日,31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗26.4亿剂次.其中26.4亿用科学记数法表示为( )A、 B、 C、 D、4. 对于下列四个立体图形,其三视图中不含有三角形的是( )A、
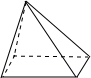 B、
B、 C、
C、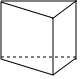 D、
D、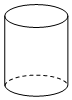 5. 如图,将三角尺的直角顶点放在直线上, , , 若直角被直线平分,则的度数是( )
5. 如图,将三角尺的直角顶点放在直线上, , , 若直角被直线平分,则的度数是( ) A、 B、 C、 D、6. a,b是两个连续整数,若 , 则a,b分别是( )A、2,3 B、3,4 C、4,5 D、5,67. 在平面直角坐标养中,若直线不经过第四象限,则关于x的方程的实数根的个数为( )A、0 B、0或1个 C、2个 D、1或2个8. 如图,四边形是菱形,边长为4, , 垂直于的直线从点A出发,沿AD方向以每秒1个单位长度的速度向右平移,设直线EF与菱形的两边分别交于点E,F(点E在点F的上方),若的面积为y,直线的运动时间为x秒(),则能大致反映y与x的函数关系的图象是( )
A、 B、 C、 D、6. a,b是两个连续整数,若 , 则a,b分别是( )A、2,3 B、3,4 C、4,5 D、5,67. 在平面直角坐标养中,若直线不经过第四象限,则关于x的方程的实数根的个数为( )A、0 B、0或1个 C、2个 D、1或2个8. 如图,四边形是菱形,边长为4, , 垂直于的直线从点A出发,沿AD方向以每秒1个单位长度的速度向右平移,设直线EF与菱形的两边分别交于点E,F(点E在点F的上方),若的面积为y,直线的运动时间为x秒(),则能大致反映y与x的函数关系的图象是( )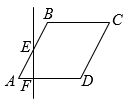 A、
A、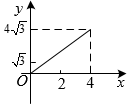 B、
B、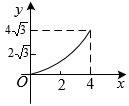 C、
C、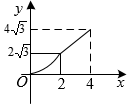 D、
D、 9. 已知三个实数a、b、c,满足 , , 且、、 , 则的最小值是( )A、 B、 C、 D、10. 如图,是一“赵爽弦图”,它是四个全等的直角三角形与中间一个小正方形拼成的大正方形,其直角三角形的两条直角边的长分别是3和5,连接 , 并向两端延长,分别交、于点E、F,则的长为( )
9. 已知三个实数a、b、c,满足 , , 且、、 , 则的最小值是( )A、 B、 C、 D、10. 如图,是一“赵爽弦图”,它是四个全等的直角三角形与中间一个小正方形拼成的大正方形,其直角三角形的两条直角边的长分别是3和5,连接 , 并向两端延长,分别交、于点E、F,则的长为( ) A、 B、4 C、 D、
A、 B、4 C、 D、二、填空题
-
11. 计算:.12. 分解因式: .13. 如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,且点A的坐标为(-2,0),D为第一象限内上的一点,若 , 则.
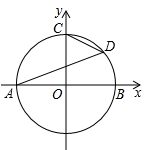 14. 设抛物线 , 其中a为实数.(1)、若抛物线经过点 , 则m=;(2)、该抛物线的顶点随着a的变化而移动,当顶点移动到最高处时,则该抛物线的顶点坐标为.
14. 设抛物线 , 其中a为实数.(1)、若抛物线经过点 , 则m=;(2)、该抛物线的顶点随着a的变化而移动,当顶点移动到最高处时,则该抛物线的顶点坐标为.三、解答题
-
15. 解方程:16. 在平面直角坐标系中,的顶点位置如图所示.
 (1)、作出关于x轴对称的图形 , 若内部一点P的坐标为 , 则点P的对应点的坐标是;(2)、将绕原点逆时针旋转得到 , 画出.17. 如图,有一宽为的旗子,小明在点D处测得点B的仰角为 , 随后小明沿坡度为的斜坡走到点E处,又测得点A的仰角为 . 已知米,米,求旗子的宽度 . (测角器的高度忽略不计,结果精确到0.1米.参考数据: , )
(1)、作出关于x轴对称的图形 , 若内部一点P的坐标为 , 则点P的对应点的坐标是;(2)、将绕原点逆时针旋转得到 , 画出.17. 如图,有一宽为的旗子,小明在点D处测得点B的仰角为 , 随后小明沿坡度为的斜坡走到点E处,又测得点A的仰角为 . 已知米,米,求旗子的宽度 . (测角器的高度忽略不计,结果精确到0.1米.参考数据: , ) 18. 观察以下等式:
18. 观察以下等式:第1个等式: ,
第2个等式: ,
第3个等式: ,
第4个等式: , ……
按照以上规律,解决下列问题:
(1)、写出第5个等式:;(2)、写出你猜想的第n个等式:(用含n的等式表示),并证明.19. 已知:正比例函数与反比例函数的图象都经过点.(1)、求k,m的值;(2)、第一象限内的点B在这个反比例函数的图象上,过点B作轴,交y轴于点C,且 , 求直线的表达式.20. 如图,已知是的外接圆,过圆心O,且 , 垂足为点F,交的延长线于点E,连接、 .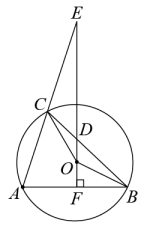 (1)、若 , 的半径长为6,求的长;(2)、求证: .21. 某校决定开展篮球、足球、乒乓球和羽毛球四种项目的活动课,为了解学生对四种项目的喜欢情况,随机调查了部分学生很喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结构绘制成如下的不完整的统计图表:
(1)、若 , 的半径长为6,求的长;(2)、求证: .21. 某校决定开展篮球、足球、乒乓球和羽毛球四种项目的活动课,为了解学生对四种项目的喜欢情况,随机调查了部分学生很喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结构绘制成如下的不完整的统计图表:学生最喜欢的活动项目的人数统计表
项目
学生数(名)
百分比
篮球
5
10%
足球
15
m%
乒乓球
n
40%
羽毛球
10
20%
根据图表中提供的信息,解答下列问题:
(1)、m= , n=;(2)、根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢乒乓球;(3)、甲、乙两名同学在这四个活动项目中任选一个活动项目参加活动课,求甲乙同时选择乒乓球活动课的概率.

