安徽省合肥市包河区2022年九年级下学期教学质量检测数学试题
试卷更新日期:2022-04-26 类型:中考模拟
一、单选题
-
1. 在数2,-2, , 中,最小的数为( )A、-2 B、 C、 D、22. 在合肥各区县2021年经济数据中,包河区GDP及人均可支配收入都领先于其他各区,成绩耀眼,包河区GDP达到1547亿元,全体居民人均可支配收入高达6.15万元,其中1547亿用科学记数法表示为( )A、1.547×1012 B、1.547×1011 C、1547×108 D、0.1547×10123. 下列运算中,正确的是( )A、 B、 C、 D、4. 如图,该几何体的左视图是( )
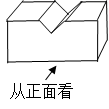 A、
A、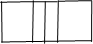 B、
B、 C、
C、 D、
D、 5. 如图,一块含有60°角的直角三角板放置在两条平行线上,若∠α=24°,则∠β为( )
5. 如图,一块含有60°角的直角三角板放置在两条平行线上,若∠α=24°,则∠β为( ) A、106° B、96° C、104° D、84°6. 为了解某校学生对篮球、足球、羽毛球、乒乓球、网球等五类球的喜受情况,小鹏采用了抽样调查,在绘制扇形图时,由于时间仓促,还有足球、网球等信息没有绘制完成,已知喜欢网球的人数少于喜欢足球的人数,根据如图所示的信息,这批被抽样调查的学生中喜欢足球的人数可能是( )
A、106° B、96° C、104° D、84°6. 为了解某校学生对篮球、足球、羽毛球、乒乓球、网球等五类球的喜受情况,小鹏采用了抽样调查,在绘制扇形图时,由于时间仓促,还有足球、网球等信息没有绘制完成,已知喜欢网球的人数少于喜欢足球的人数,根据如图所示的信息,这批被抽样调查的学生中喜欢足球的人数可能是( ) A、120人 B、140 人 C、150 人 D、290人7. 为满足人们对防疫物资的需求,某口罩加工厂增加设备,努力提高口罩生产量,2021年10月份该工厂的口罩产量为500万个,12月份产量为604万个,若月平均增长串相同,则月平均增长率约是( )A、9% B、10% C、12% D、21%8. 如图,点A在双曲线y=(x>0)上,点B在双曲线y=(x>0)上,轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是15,则k的值为( )
A、120人 B、140 人 C、150 人 D、290人7. 为满足人们对防疫物资的需求,某口罩加工厂增加设备,努力提高口罩生产量,2021年10月份该工厂的口罩产量为500万个,12月份产量为604万个,若月平均增长串相同,则月平均增长率约是( )A、9% B、10% C、12% D、21%8. 如图,点A在双曲线y=(x>0)上,点B在双曲线y=(x>0)上,轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是15,则k的值为( ) A、21 B、18 C、15 D、99. 如图,O是矩形ABCD的对角线交点,AE平分∠BAD,∠AOD=120°,∠AEO的度数为( )
A、21 B、18 C、15 D、99. 如图,O是矩形ABCD的对角线交点,AE平分∠BAD,∠AOD=120°,∠AEO的度数为( ) A、15° B、25° C、30° D、35°10. 将函数y=-2x+b(b为常数)的图象位于x轴上方的部分沿x轴翻折至其下方,所得的折线记为图象C,若图象C在直线y=-3上方所有点(含交点)的横坐标x均满足0≤x≤4,则b的取值范围是( )A、3≤b≤5 B、0≤b≤3 C、0<b<3 D、3<b<5
A、15° B、25° C、30° D、35°10. 将函数y=-2x+b(b为常数)的图象位于x轴上方的部分沿x轴翻折至其下方,所得的折线记为图象C,若图象C在直线y=-3上方所有点(含交点)的横坐标x均满足0≤x≤4,则b的取值范围是( )A、3≤b≤5 B、0≤b≤3 C、0<b<3 D、3<b<5二、填空题
-
11. 计算:=12. ρ=≈1.3247195724……是一个著名的常数,别称为Plastic number,它是一元三次方程x=x+1的唯一实数根,这个实数中蕴含无理数 , 已知n-1<<n(n为正整数),则n的值是13. 如图,在等腰ABO中,AO=AB,OB=6,以OB为半径作⊙O交AB于点C,若BC=4,则cosA=
 14. 在ABC中,∠C=60°,D是边AB的中点,E是边BC上一点,连接DE,DE=2(1)、若点E为BC的中点,则AC=;(2)、若DE平分ABC的周长,则AC=
14. 在ABC中,∠C=60°,D是边AB的中点,E是边BC上一点,连接DE,DE=2(1)、若点E为BC的中点,则AC=;(2)、若DE平分ABC的周长,则AC=三、解答题
-
15. 解不等式:>x+116. 先化简、再求值: , 其中a=217. 如图,在平面直角坐标系中,ABC 的三个顶点坐标分别为A(-2,1)、B(-1,4)、C(-3,3)
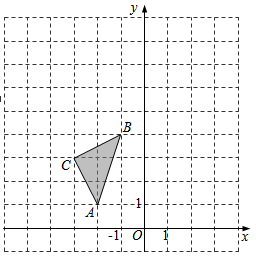
(1)画出ABC关于y轴对称的A1B1C1;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出将ABC放大后的A2B2C2;直接写出点C2的坐标.
18. 如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需要绕行B地,已知B位于A地北偏东67°方向,距离A地520 km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)参考数据:(sin67°≈;cos67°≈;tan67°≈;≈1.73) 19. 如图,某学校准备新建一个读书长廊,井用若干块带有花纹和没有花纹的两种规格、大小相同的正方形地砖搭配在一起,按图中所示的规律拼成图案铺满长廊,已知每个小正方形地砖的边长均为0.5米.
19. 如图,某学校准备新建一个读书长廊,井用若干块带有花纹和没有花纹的两种规格、大小相同的正方形地砖搭配在一起,按图中所示的规律拼成图案铺满长廊,已知每个小正方形地砖的边长均为0.5米. (1)、按图示规律,第3图案的长度L3=;第3个图案中没有花纹的正方形地砖数为 .(2)、若某个图案中带有花纹的地砖为n块,则没有花纹的地砖为块.(用含n的代数式表示)(3)、若学校读书长廊的长度为Ln=100.5米,求没有花纹的正方形地砖有多少块?20. 如图,AB为⊙O的直径,直线BM⊥AB于点B,点C在⊙O上,分别连接BC,AC,且AC的延长线交BM于点D,CF为⊙O的切线交BM于点F.
(1)、按图示规律,第3图案的长度L3=;第3个图案中没有花纹的正方形地砖数为 .(2)、若某个图案中带有花纹的地砖为n块,则没有花纹的地砖为块.(用含n的代数式表示)(3)、若学校读书长廊的长度为Ln=100.5米,求没有花纹的正方形地砖有多少块?20. 如图,AB为⊙O的直径,直线BM⊥AB于点B,点C在⊙O上,分别连接BC,AC,且AC的延长线交BM于点D,CF为⊙O的切线交BM于点F. (1)、求证:CF=DF;(2)、连接OF,若AB=10,BC=6,求线段OF的长.21. 某校近期对七、八年级学生进行了“新型冠状病毒防治知识”线上测试,为了解他们的掌握情况,从七、八年级各随机抽取了50名学生的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息:
(1)、求证:CF=DF;(2)、连接OF,若AB=10,BC=6,求线段OF的长.21. 某校近期对七、八年级学生进行了“新型冠状病毒防治知识”线上测试,为了解他们的掌握情况,从七、八年级各随机抽取了50名学生的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息:a、七年级的频数分布直方图如图(数据分为5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90, 90≤x≤100)
b、七年级学生成绩在80≤x<90的这一组是:80;80.5;81;82;82;83;83.5;84;84;85;86;86.5;87;88; 89;89
c、七、八年级学生成绩的平均数、中位数、众数如表:

年级
平均数
中位数
众数
七年级
85.3
m
90
八年级
87.2
85
91
根据以上信息,回答下列问题:
(1)、表中m的值为;(2)、在随机抽样的学生中,七年级小张同学与八年级小李同学的成绩都为84分,请问谁在自己的年级排名更靠前?请说明理由;(3)、七年级学生中,有2位女同学和1位男同学获得满分,这3位同学被授予“疫情防控标兵”称号,并安排在领奖台上随意排成一排拍照留念,求两名女生不相邻的概率.
