安徽省安庆市2022年九年级毕业班中考模拟数学试题

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣6的相反数是（　　）

A、﹣6 B、﹣ $\frac{1}{6}$ C、6 D、 $\frac{1}{6}$

查看试题解析
2. 下列计算正确的是（）

A、 $x^{2} + x = x^{3}$ B、 $x^{2} \cdot x = x^{3}$ C、 $x^{2} - x = x^{3}$ D、 $x^{2} \div x = x^{3}$

查看试题解析
3. 2022年1月31日，农历除夕，中国人首次在距离地球约396000米的“中国宫”里迎新春、过大年．神舟十三号航天员在遥远的太空专门发来视频，向祖国和人民送上祝福．数据396000用科学记数法表示为（）

A、 $3.96 \times 1 0^{5}$ B、 $3.96 \times 1 0^{6}$ C、 $396 \times 1 0^{3}$ D、 $39.6 \times 1 0^{4}$

查看试题解析
4. 如图所示的几何体是由一块大正方体截去一个小正方体得到的，该几何体的主视图是（）

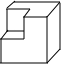A、 B、 C、 D、

查看试题解析
5. 如图所示，已知 $A B ∥ C D$ ， EF平分∠CEG，若 $∠ 1 = 70 °$ ，则∠GFE的度数为（）

A、 $60 °$ B、 $45 °$ C、 $55 °$ D、 $70 °$

查看试题解析
6. 某市中考体育项目有：中长跑（1000米/男生、800米/女生）、坐位体前屈、立定跳远、一分钟跳绳、掷实心球、篮球运球、足球运球．其中中长跑设定为必考项目，考生可以在余下六个项目中自主选择2个不同的项目进行考试，则恰好选中坐位体前屈和一分钟跳绳的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{36}$ C、 $\frac{1}{30}$ D、 $\frac{1}{15}$

查看试题解析
7. 某工厂计划用两年时间使产值增加到目前的3倍，并且使第二年增长率是第一年增长率的2倍，设第一年增长率为x，则可列方程得（）

A、 ${(1 + x)}^{2} = 3$ B、 $x (1 + 2 x) = 3$ C、 $2 x (1 + x) = 3$ D、 $(1 + x) (1 + 2 x) = 3$

查看试题解析
8. 已知a，b为不同的两个实数，且满足 $a b > 0$ ， $a^{2} + b^{2} = 9 - 2 a b$ ，当 $a - b$ 为整数时，ab的值为（）

A、 $\frac{5}{4}$ 或2 B、 $\frac{9}{4}$ 或 $\frac{5}{4}$ C、 $\frac{1}{4}$ 或2 D、 $\frac{9}{4}$ 或2

查看试题解析
9. 如图，⊙O的半径为3，边长为2的正六边形ABCDEF的中心与O重合，M、N分别是AB、FA的延长线与⊙O的交点，则图中阴影部分的面积是（）

A、 $π - \sqrt{3}$ B、 $\frac{3}{2} π - \sqrt{3}$ C、 $\frac{9}{4} π - \sqrt{3}$ D、 $\frac{9}{4} π - \frac{\sqrt{3}}{2}$

查看试题解析
10. 已知：抛物线 $y = - x^{2} - 4 x + 5$ 与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．平行于x轴的直线l与该抛物线交于点D $(x_{1} ， y_{1})$ ， E $(x_{2} ， y_{2})$ ，与线段AC交于点F $(x_{3} ， y_{3})$ ，令 $g = \frac{x_{3}}{x_{1} + x_{2}}$ ，则g的取值范围是（）

A、 $0 \leq g \leq \frac{5}{2}$ B、 $- \frac{5}{2} \leq g \leq 0$ C、 $0 \leq g \leq \frac{5}{4}$ D、 $- \frac{5}{4} \leq g \leq 0$

查看试题解析

二、填空题

11. 计算： $\sqrt{18} - \sqrt{8} =$ .

查看试题解析
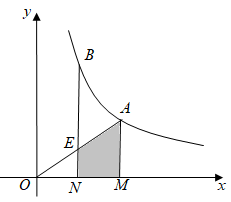
12. 因式分解： $m^{2} n - 10 m n + 25 n =$ ．

查看试题解析
13. 如图，已知A，B是函数 $y = \frac{k}{x}$ （x＞0）图象上的两点，点B位于点A的左侧，AM，BN均垂直于x轴，垂足为点M，N，连接AO，交BN于点E，若 $N E = \frac{1}{3} N B$ ，四边形AMNE的面积为2，则k的值为．

查看试题解析
14. 如图，在 $△ A B C$ 中， $A C = 4$ ， $∠ C A B = 45 °$ ， $∠ A C B = 60 °$ ， D是 $A B$ 的中点，直线l经过点D， $A E ⊥ l$ 于点E， $C F ⊥ l$ 于点F．

(1)、若 $l ⊥ A B$ ，则 $A E + C F =$ ；

(2)、当直线l绕点D旋转时， $A E + C F$ 的最大值为．

查看试题解析

三、解答题

15. 解不等式： $x \leq \frac{3 - x}{2}$ ．

查看试题解析
16. 电影《水门桥》正在热映，票价每张40元，购买50人以上的团体票，有两种优惠方案可供选择，方案一：全体人员可打8折；方案二：n人免票，其余人员打9折，901班共有54人，无论选择哪种优惠方案购票观看，所付费用相同，求优惠方案二中的免票人数n．

查看试题解析
17. 观察下列等式：
第1个等式： $1 - \frac{3}{4} = \frac{1}{1 \times 4}$ ；

第2个等式： $\frac{1}{2} - \frac{3}{7} = \frac{1}{2 \times 7}$ ；

第3个等式： $\frac{1}{3} - \frac{3}{10} = \frac{1}{3 \times 10}$ ；

第4个等式： $\frac{1}{4} - \frac{3}{13} = \frac{1}{4 \times 13}$ ；

…

根据你观察到的规律，解决下列问题：

(1)、请写出第5个等式：；

(2)、请写出第n个等式（用含n的等式表示），并证明．

查看试题解析
18. 如图，在边长是1个单位长度的小正方形组成的 $4 \times 3$ 网格中，给出了以格点（网格线的交点）为端点的线段AB．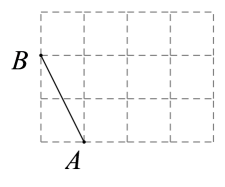
( 1 )将线段AB绕点A顺时针旋转90°得到线段 $A B_{1}$ ，请画出线段 $A B_{1}$ ；
( 2 )作出点A关于直线 $B B_{1}$ 的对称点 $A_{1}$ ，并画出四边形 $A B A_{1} B_{1}$ ；
( 3 )以格点为顶点的四边形称为“格点四边形”，在所给的网格中，还能作出 ▲ 个与四边形 $A B A_{1} B_{1}$ 全等的“格点四边形”（不作图）．

查看试题解析
19. 坐落在长江边上的安庆振风塔号称“万里长江第一塔”，塔七层八角．如图，为了测量楼层的高度，在4楼底部“塔的中轴线上点B处”测得地面上点P的俯角为35°，在5楼底部“塔的中轴线上点A处”测得点P的俯角为40°，已知塔基直径MN为20米，点P到塔基边缘的最近距离PM为30米，求塔的第4层高度AB．（参考数据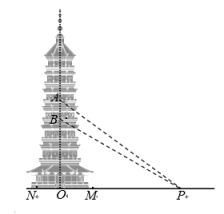： $t a n 35 ° \approx 0.70$ ， $t a n 40 ° \approx 0.84$ ）

查看试题解析
20. 如图，四边形ABCD内接于⊙O，对角线AC与BD相交于点E，直线AM与⊙O相切于点A，交CB延长线于M，弦 $B D ∥ A M$ ．

(1)、求证：∠MAB＝∠ACD；

(2)、若AB＝5，BD＝8，求⊙O的半径．

查看试题解析
21. 为落实课后服务工作的相关要求，某学校于周一下午同时开设了四门特色课程供七年级学生选择（每个学生必选且只选一门）：A．花样跳绳；B．趣味地理；C．创意剪纸；D．音乐欣赏．该校七年级学生共有450人，全体七年级学生的选课情况统计如图①．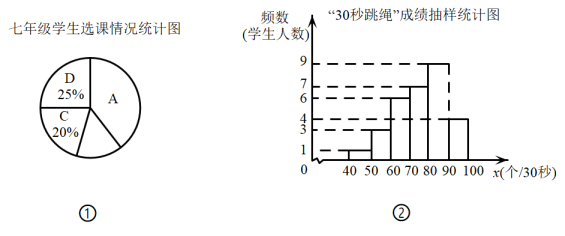

(1)、求该校七年级学生中选择A课程的学生共有多少人？

(2)、为了解A课程的学习效果，对七年级选择A课程的所有学生进行了一次“30秒跳绳”成绩检测，并从中随机抽取了30名学生的“30秒跳绳”成绩进行统计，将他们的成绩绘制成频数分布直方图（如图②）．
①其中 $70 \leq x < 80$ 这一组的数据为75，72，73，74，77，77，79，则这组数据的中位数是 ▲ ，众数是 ▲ ；

②根据以上信息，估计七年级选择A课程的所有学生本次检测的“30秒跳绳”成绩超过77个的有多少人？

查看试题解析
22. 如图所示，“大跳台滑雪”运动中，运动员的起跳高度OA为86米，在平面直角坐标系xOy中，运动员自“起跳点A”起跳后的运行轨迹（图中虚线部分）的表达式为 $y = a x^{2} + \frac{2}{5} x + 86$ （a＜0），线段MN为“着落坡”，其表达式为 $y = - \frac{4}{5} x + 110$ ， “着落坡”上的起评分点为“K点”，“K点”离y轴的水平距离是115米．评分规则规定：当运动员的着落点H离y轴的水平距离与“K点”离y轴的水平距离之差为m米时，该运动员所得的“距离分”为 $60 + 1.8 m$ ．

(1)、某运动员的“距离分”为69分，求该运动员的着落点H离y轴的水平距离；

(2)、当运动员的“距离分”为69分时，a的值是多少？

(3)、当运动员的“距离分”为69分时，运动员运行的最高点离x轴的距离是多少？

查看试题解析
23. 如图①，在菱形ABCD中，∠BAD＝60°，点E在边AB上，点F在BD的延长线上，BE＝DF，EF与AD相交于点G，连接CE，CF．

(1)、求证：CE＝CF；

(2)、求证：△DFG∽△DCF；

(3)、如图②，连接CG，若AB＝4，点E是AB的中点，求CG长．

查看试题解析