陕西省宝鸡市2022年初中学业水平模拟考试数学试题（三）

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算(-3)×(-5)的结果是（）

A、15 B、-15 C、8 D、-8

查看试题解析
2. 2019年12月我国爆发了新冠疫情，直到2021年11月25日，我国累计治愈118944个人，这个数据用科学记数法表示为（）

A、11.8944× $1 0^{4}$ B、1.18944× $1 0^{5}$ C、0.118944× $1 0^{6}$ D、1.18944× $1 0^{6}$

查看试题解析
3. 计算： $(- \frac{1}{3} x y^{2})^{3} =$ （）

A、 $- \frac{1}{9} x^{3} y^{6}$ B、 $- \frac{1}{27} x^{3} y^{6}$ C、 $\frac{1}{27} x^{3} y^{6}$ D、 $27 x^{3} y^{6}$

查看试题解析
4. 如图所示，AE//BC，EF⊥BD，垂足为E， $∠ 1 = 28 °$ ，则∠2的度数为（）

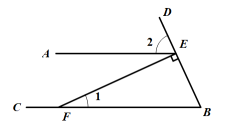A、30° B、40° C、62° D、50°

查看试题解析
5. 如图，平行四边形ABCD的对角线AC与BD相交于点O，AB⊥AC，若AB＝3，AC＝8，则BD的长是（）

A、8 B、9 C、10 D、12

查看试题解析
6. 若正比例函数 $y = k x (k \neq 0)$ 的图形经过A（m，4），B（m＋3，10）两点，则 $k$ 的值为（）

A、 $- \frac{3}{4}$ B、 $- \frac{4}{3}$ C、－2 D、2

查看试题解析
7. 如图，在△ABC中，AB＝AC，AD平分∠BAC，点E是AD上的点，且AE＝EC，若∠BAC＝45°，BD＝3，则CE的长为（）

A、3 B、 $3 \sqrt{2}$ C、 $2 \sqrt{3}$ D、4

查看试题解析
8. 在平面直角坐标系中，抛物线C₂是由抛物线C₁沿x轴平移得到的，它们的交点坐标为（－1，a），若抛物线C₁表达式为 $y = m x^{2} - 6 m x + n (m \neq 0)$ ，则抛物线C₂的顶点坐标为（）

A、（－4，n－9m） B、（－4，9m－n） C、（－5，n－9m） D、（－5，9m－n）

查看试题解析

二、填空题

9. 分解因式： $8 x^{2} - 2 =$ ．

查看试题解析
10. 若某正多边形的一条边长是4，一个外角为45°，则该正多边形的周长为．

查看试题解析
11. 如图是正方体的一种展开图，则原正方体中与“真”所在面的对面所标的字是．

查看试题解析
12. 已知A、B两点分别在反比例函数 $y = \frac{2 m}{x} (m \neq 0)$ 和 $y = \frac{6 m - 1}{x} (m \neq \frac{1}{6})$ 的图像上，若点A与点B关于x轴对称，则m的值为．

查看试题解析
13. 如图，在矩形ABCD中，AB＝6，BC＝8，点E、F分别是边AB、BC上的动点，且EF＝4，点G是EF的中点，AG、CG，则四边形AGCD面积的最小值为．

查看试题解析

三、解答题

14. 计算： $| \sqrt{2} - 2 | - 2 c o s 4 5^{∘} + \sqrt{18} - 8 \times 2^{- 2}$

查看试题解析
15. 解不等式组： ${\begin{array}{l} 3 x + 2 > 2 x - 3 \\ \frac{x - 1}{3} \leq 5 - \frac{4}{3} x \end{array}$

查看试题解析
16. 解方程： $\frac{2}{x^{2} - 1} + 1 = \frac{x}{x + 1}$

查看试题解析
17. 如图，已知Rt△ABC中，∠A＝30°，请用尺规作图法，在AC边上求做一点M使MA＝2MC（不写做法，保留作图痕迹）

查看试题解析
18. 如图，AB∥CD，E是CD上一点，BE交AD于点F，EF＝BF.求证：AF＝DF.

查看试题解析
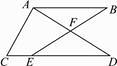19. 2020年是脱贫攻坚的收官之年，某县的扶贫项目“小木耳，大产业”一时红遍全国．王林及家人为了助力扶贫攻坚，打算去参观该县的“木耳产业园”，并购买新鲜木耳．经了解，进园参观费每人20元，购买新鲜的木耳在2千克以内，每千克70元；超过2千克的，超过部分每千克60元，设王林和爸爸妈妈一家三口进入该木耳产业园参观并购买新鲜的木耳x千克，共付费y元．

(1)、求y与x之间的函数关系式；

(2)、若王林一家共付费416元，则王林一家共购买了多少千克木耳？

查看试题解析
20. 第十四届全国运动会于2021年在陕西已经召开，第十四届全运会的会徽取象传统礼天玉壁，吉祥物设计方案是以陕西秦岭独有的四个国宝级动物“朱鹮、大熊猫、羚牛、金丝猴”为创意原型．现有五张形状相同的不透明纪念卡片分别绘有“会徽”、“朱朱”、“熊熊”、“羚羚”、“金金”吉祥物的图案．纪念卡背面完全相同，将卡片洗匀背面超长．

(1)、乐乐从纪念卡中任意摸一张，则摸到绘有“朱朱”的概率为．

(2)、如果乐乐摸两次（第一次摸出后记录并放回），请用画树状图或列表的方法求乐乐两次摸到属于“秦岭四宝”的纪念卡的概率．

查看试题解析
21. 宝鸡市凤翔区于2020年1月29日撤县建区，今天的凤翔区经济发展飞速，历史悠久．相传秦穆公之女弄玉善于吹笛，引来善于吹箫的隐士萧史，知音相遇，终成眷属，后乘凤凰飞翔而去，唐时取此意更名为凤翔．而在东大街的中央处有一座凤凰标志．在一次课外活动中，甲、乙两位同学想要测量它的高度，他们分别在A、B两处用高度1.8米的测角仪测得标志顶部C的仰角分别为30°、60°，点A、F、B在同一水平线上，且AB＝10m，AD⊥AB，BE⊥AB，求凤凰标志的高度CF（结果保留根号）．

查看试题解析
22. 为了使学生能对闲置书籍进行的合理分配，养成节约环保的意识，同时也培养学生的爱心，某校积极参加“希望工程”捐书活动，为了了解学生所捐书本情况，随机抽取了部分学生进行抽样调查，根据调查结果，绘制了如下两本不完整的统计图，请根据相关信息，解答下列问题：

(1)、请补全上面两幅统计图；

(2)、这组学生所捐书本数的众数为本，中位数为本；

(3)、请利用这个样本的平均数，估计该校参加此次捐书活动的800名学生共捐书多少本？

查看试题解析
23. 红色教育呼唤有志青年挑战自我，超越自我，奉献社会的崇高精神，不忘初心，牢记使命．陕西省延安革命纪念馆是著名的红色教育基地之一．某日，小李驾车从家出发送朋友前往该纪念馆，在途中休息了半个小时后，继续以相同的速度前往纪念馆．将朋友送达后小李立即按照原路返回，小李离家的距离y（千米）与所用时间x（小时）之间的函数关系如图所示．请根据图象，解决下列问题：

(1)、求BC段的函数关系式；

(2)、小李出发5小时后离家多远？

查看试题解析
24. 如图，AB为⊙O的直径，⊙O过AC的中点D，DE⊥BC，垂足为点E，

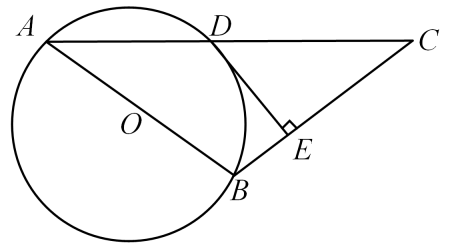(1)、求证：DE为⊙O的切线；

(2)、若⊙O的直径AB＝5，tanC＝ $\frac{1}{2}$ ，求DE得长度．

查看试题解析
25.
如图，已知抛物线y=ax²+bx+c（a≠0）经过A（﹣1，0）、B（3，0）、C（0，﹣3）三点，直线l是抛物线的对称轴．

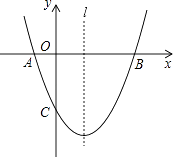(1)、求抛物线的函数关系式；

(2)、设点P是直线l上的一个动点，当点P到点A、点B的距离之和最短时，求点P的坐标；

(3)、点M也是直线l上的动点，且△MAC为等腰三角形，请直接写出所有符合条件的点M的坐标．

查看试题解析
26. 问题探究

(1)、请在图①、图② 各作两条直线，使它们将正方形ABCD与半⊙O的面积三等分；

(2)、如图③，在矩形ABCD中，AB＝3，BC＝4，请在图③中过顶点A作两条直线，使它们将矩形ABCD的面积三等分，并说明理由；
问题解决

(3)、位于宝鸡市凤翔区的机场将计划于2024年建成通航．如图④，在机场旁边有一块平行四边形ABCD空地，其中AB＝AC＝100米，BC＝120米，根据视觉效果和花期特点，机场设计部门想在这块空地上种上等面积的三种不同的花，要求从入口点A处修两条笔直的小路（小路面积忽略不计）方便旅客赏花，两条小路将这块空地的面积三等分．那么设计部门能否实现自己的想法？若能实现，请通过计算，画图说明；若不能，请说明理由．

查看试题解析