陕西省渭南市富平县2022年中考数学一模试题

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列实数是无理数的是（）

A、﹣π B、0 C、 $\sqrt{9}$ D、 $\frac{1}{2}$

查看试题解析
2. 如图所示的圆柱的左视图是（）

A、 B、 C、 D、

查看试题解析
3. 国家卫健委数据显示，截至2022年3月10日，31个省（自治区、直辖市）和新疆生产建设兵团累计报告接种新冠病毒疫苗3180060000剂次．将数据3180060000用科学记数法表示为（）

A、3.18006×10¹⁰ B、3.18006×10⁹ C、31800.6×10⁵ D、318006×10⁴

查看试题解析
4. 将一副三角板 $(∠ A = 30 ° ， ∠ E = 45 °)$ 按如图所示方式摆放，使得 $A C ∥ E F$ ，则 $∠ D O B$ 等于（）

A、 $75 °$ B、 $105 °$ C、 $60 °$ D、 $90 °$

查看试题解析
5. 已知点A（2，y₁）和点B（a，y₂）在一次函数y＝﹣3x﹣b的图象上，且y₁＞y₂ ，则a的值可能是（）

A、3 B、0 C、﹣1 D、﹣2

查看试题解析
6. 如图，点A ， B ， C在 $⊙ O$ 上，四边形 $O A B C$ 是平行四边形．若对角线 $A C = 2 \sqrt{3}$ ，则 $\overset{⌢}{A C}$ 的长为（）

A、 $\frac{3 π}{2}$ B、 $\frac{5 π}{3}$ C、 $\frac{4 π}{3}$ D、 $\frac{4 \sqrt{3} π}{3}$

查看试题解析
7. 点P(m，n)在以y轴为对称轴的二次函数y＝x²+ax+4的图象上.则m﹣n的最大值等于（）

A、 $\frac{15}{4}$ B、4 C、﹣ $\frac{15}{4}$ D、﹣ $\frac{17}{4}$

查看试题解析

二、填空题

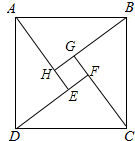
8. 计算：（﹣a⁰）²⁰²²＝．（a≠0）

查看试题解析
9. 过十边形的一个顶点，可以引出对角线的条数为．

查看试题解析
10. 如图是“赵爽弦图”，△ABH，△BCG，△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形，如果AB＝15，且AH：AE＝3：4，那么△DFC周长等于．

查看试题解析
11. 如图，在△ABC中，AB＝AC＝4，∠BAC＝120°，AD是△ABC的中线，AE是∠BAD的平分线，过点D作DF∥AB交AE的延长线于点F，则DF的长为．

查看试题解析
12. 已知反比例函数 $y = - \frac{6}{x}$ 的图象上有两点A（x₁ ， y₁），B（x₂ ， y₂）．若x₁y₂＝﹣3，则x₂y₁的值为．

查看试题解析
13. 如图，点O是平行四边形ABCD的对称中心，点E、F分别为边BC、AD上任意一点，且O、E、F三点在一条直线上，连接AO，BO，EO，FO．若AB＝4，BC＝6，∠ABC＝60°，则图中阴影部分的面积是．

查看试题解析

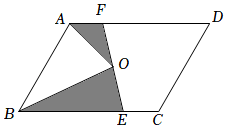
三、解答题

14. 计算： $(- \frac{1}{3})^{- 2} - \sqrt{3} \times \sqrt{27} + | 3 - π |$ ．

查看试题解析
15. 化简：（2x﹣3）（2x＋3）﹣（2x﹣1）²

查看试题解析
16. 解一元一次不等式组： ${\begin{array}{l} 3 - 2 x < 5 \\ \frac{x + 4}{3} \geq x \end{array}$ ．

查看试题解析
17. 如图，在△ABC中，DE垂直平分BC．请用尺规作图法，在线段DE上求作一点P，使点P到线段AB、BC的距离相等．（保留作图痕迹，不写作法）

查看试题解析
18. 解方程 $\frac{x - 3}{x - 2} + 1 = \frac{2}{2 - x}$

查看试题解析
19. 如图，点C、E、F、B在同一条直线上，CE＝BF，AB＝DC，AB∥DC．求证：∠A＝∠D．

查看试题解析
20. 近期某高校为保护学生和教师的健康，进行了“抗疫物资”储备，用19000元购进甲、乙两种医用口罩共计900盒，且甲、乙两种口罩的售价分别是20元/盒，25元/盒．求甲、乙两种口罩各购进了多少盒？

查看试题解析
21. 第二十四届冬奥会于2022年2月20日在北京闭幕，北京成为全球首个既举办过夏季奥运会又举办过冬季奥运会的城市．如图，是四张关于冬奥会运动项目的卡片，卡片的正面分别印有A．“花样滑冰”、B．“高山滑雪”、C．“单板滑雪大跳台”、D．“钢架雪车”（这四张卡片除正面图案外，其余都相同）．将这四张卡片背面朝上，洗匀．

(1)、从中随机抽取一张，抽得的卡片恰好为“花样滑冰”的概率为；

(2)、若先从中随机抽取一张，记录这张卡片上图案的运动项目后放回，背面朝上，洗匀．再从中随机抽取一张，请你用列表或画树状图的方法，求这两次抽取的卡片图案上是“单板滑雪大跳台”和“钢架雪车”运动项目的概率．

查看试题解析
22. 本学期开学后，某校为了激发学生进行体育活动的积极性，提高学生身体素质，对九年级学生进行了1分钟“跳绳”项目摸底测试，同时统计了每个人的跳绳个数（设为x）．现在将这些同学中女生的测试结果随机抽取若干个成绩进行分析，分为四个等级：A．优秀（x≥170）、B．良好（145≤x≤169）、C．及格（120≤x≤144）和D．不及格（x≤119），并将统计结果绘制成如图两幅不完整的统计图．
请你根据以上信息，解答下列问题：

(1)、补全如图的条形统计图和扇形统计图；

(2)、被测试女生1分钟“跳绳”个数的中位数落在等级；

(3)、如果该校九年级现有女生500人，请估计该校九年级女生中1分钟“跳绳”个数达到优秀的人数．

查看试题解析
23. 风筝起源于春秋战国时期，至今已有两千多年．星期日，小明（A）与小丽（B）两人来到广阔的草原，一前一后在水平地面AD上放风筝，结果风筝在空中C处纠缠在一起，如图所示，测得∠CAD＝30°，∠CBD＝60°，且小丽、小明之间的距离AB＝20m，求此时风筝C处距离地面的高度．（参考数据： $\sqrt{3} \approx$ 1.732，结果保留一位小数）

查看试题解析
24. 某年级430名师生秋游，计划租用8辆客车，现有甲、乙两种型号客车，它们的载客量和租金如下表：

甲种客车
乙种客车
载客量（座/辆）
60
45
租金（元/辆）
550
450

(1)、设租用甲种客车x辆，租车总费用为y元．求出y（元）与x（辆）之间的函数表达式；

(2)、当甲种客车有多少辆时，能保障所有的师生能参加秋游且租车费用最少，最少费用是多少元？

查看试题解析
25. 如图，已知直线PA交⊙O于A、B两点，AE是⊙O的直径，点C为⊙O上一点，且AC平分∠PAE．

(1)、过点C作⊙O的切线交BP于点D，求证：CD⊥PA；

(2)、若⊙O的半径为5，AB＝6，求BD的长．

查看试题解析
26. 如图，抛物线y＝ax²＋5x＋c交x轴于点A（1，0）、B，交y轴于点C（0，﹣4）．

(1)、求该抛物线的表达式；

(2)、若P是抛物线上x轴上方的一动点，过P作PM⊥x轴，垂足为M．是否存在P点，使得以A，P，M为顶点的三角形与△OBC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．

查看试题解析
27. 如图

(1)、【问题提出】如图①，点A为线段BC外一动点，且BC＝a，AB＝b，则线段AC的最大值为；（用含a，b的式子表示）

(2)、【问题探究】如图②，点A为线段BC外一动点，且BC＝6，AB＝3，分别以AB，AC为边，作等边三角形ABD和等边三角形ACE，连接CD，BE，找出图中与BE相等的线段，请说明理由，并求出线段BE长的最大值；

(3)、【问题解决】如图③，某市区有一块空地，为了美化环境，计划设计一个不规则的四边形景观区域ABCD．根据实际情况，要求AB＝AD，∠BAD＝60°，且对角线BD⊥CD于点D，为尽量增加游客观赏时间、提高观赏体验感，计划在景观区域内部沿对角线AC修一条小道．已知BC＝40m，求AC的最大值．

查看试题解析

	甲种客车	乙种客车
载客量（座/辆）	60	45
租金（元/辆）	550	450