陕西省西安市莲湖区2022年九年级中考第一次模拟数学试题

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，比-1小的数是（）

A、-4 B、0 C、-1 D、1

查看试题解析
2. 如图，该几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列式子中，与 $a^{3} \cdot a^{5}$ 相等的是（）

A、 $a^{30} \div a^{2}$ B、 $a^{5} + a^{3}$ C、 $a^{4} \cdot a^{2}$ D、 ${(a^{4})}^{2}$

查看试题解析
4. 某商店连续7天销售口罩的盒数分别为9，11，13，12，11，11，10．关于这组数据，以下结论错误的是（）

A、众数是11 B、平均数是11 C、中位数是12 D、方差是 $\frac{10}{7}$

查看试题解析
5. 点P的坐标为 $(6 ， 2)$ ， A是x轴正半轴上一点，O为原点，则 $c o s ∠ A O P$ 的值为（）

A、3 B、 $\frac{3 \sqrt{10}}{10}$ C、 $\frac{\sqrt{10}}{10}$ D、 $\frac{1}{3}$

查看试题解析
6. 如图，直线 $a ∥ b$ ，一块含45°角的直角三角板的直角顶点恰好在直线a上，若 $∠ 1 = 25 °$ ，则∠2的度数是（）

A、50° B、60° C、70° D、80°

查看试题解析
7. 若点 $A (a ， y_{1})$ ， $B (a + 1 ， y_{2})$ 在反比例函数 $y = \frac{k}{x} (k < 0)$ 的图象上，且 $y_{1} > y_{2}$ ，则 $a$ 的取值范围是（）

A、 $a < - 1$ B、 $- 1 < a < 0$ C、 $a > 0$ D、 $a < - 1$ 或 $a > 0$

查看试题解析
8. 已知抛物线 $C ： y = x^{2} - 4 m x + m - 3$ ，其顶点为D，若点D到x轴的距离为3，则m的值为（）

A、0或 $\frac{1}{4}$ B、 $\frac{3}{4}$ C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$ 或 $- \frac{3}{4}$

查看试题解析

二、填空题

9. 计算： $- 1^{2} + 2 \times | - 4 | =$ ．

查看试题解析
10. 分解因式： $x^{2} y - 6 x y + 9 y$ = ．

查看试题解析
11. 我国明代数学读本《算法统宗》中有这样一道题：一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托．问：索子与竿子分别长多少托？若设索子长 $x$ 托，竿子长 $y$ 托，则列方程组为．

查看试题解析
12. 如图，在 $△ A B C$ 中，CD，BE是 $△ A B C$ 的两条中线，则 $\frac{S_{△ D E F}}{S_{△ B C F}}$ 的值为．

查看试题解析
13. 如图，等边△ABC的边长为6，三角形内部有一个半径为1的 $⊙ P$ ，若含 $⊙ P$ 与△ABC边相切的情况，则点P可移动的最大范围（最大面积）是．

查看试题解析

三、解答题

14. 计算： $\sqrt{2} c o s 45 ° + {(1 - π)}^{0} + \sqrt{\frac{1}{16}} + | 1 - \sqrt{2} |$ ．

查看试题解析
15. 解不等式组： ${\begin{array}{l} x + 4 > - 2 x + 1 ， \\ \frac{x}{2} - \frac{x - 1}{3} \leq 1 . \end{array}$

查看试题解析
16. 解方程： $\frac{x}{x - 2} - \frac{8}{x^{2} - 2 x} = 1$ ．

查看试题解析
17. 如图所示的是以O为圆心的圆， $⊙ O$ 上有一点A，请用尺规作图法，求作 $⊙ O$ 的内接正方形ABCD．（保留作图痕迹，不写作法）

查看试题解析
18. 如图，在△ABC中，点D在BC的延长线上， $D E ∥ A C$ ，且 $D E = B C$ ， $A C = B D$ ．求证： $△ A B C ≌ △ B E D$ ．

查看试题解析
19. 香香猪肉铺10月五花肉售价约30元/千克，后受市场供需关系影响，五花肉价格逐月上涨，12月五花肉售价约为36.3元/千克，若在此期间五花肉价格每月增长率相同．

(1)、求此期间五花肉价格月增长率．

(2)、11月某天小刚妈妈用99元在香香猪肉铺买了一些五花肉包饺子，请问她买了多少五花肉．

查看试题解析
20. 2022年冬奥会吉祥物为“冰墩墩”，冬残奥会吉祥物为“雪容融”，如图，现有三张正面印有吉祥物的不透明卡片，卡片除正面图案不同外，其余均相同，其中两张正面印有冰墩墩图案的卡片分别记为 $A_{1}$ 、 $A_{2}$ ，另一张正面印有雪容融图案的卡片记为B，将三张卡片正面向下洗匀，冬冬同学从中随机抽取一张卡片，记下图案后正面向下放回，洗匀后再从中随机抽取一张卡片．

(1)、从这三张卡片中随机挑选一张，是“雪容融”的概率是．

(2)、试用画树状图或列表的方法表示所有可能的结果，求冬冬同学两次抽出的卡片都是冰墩墩卡片的概率．

查看试题解析
21. 如图，某海轮在港口A处观测到在其北偏东50°有一灯塔P，海轮早上8：00从港口A出发沿北偏东70°的方向航行，11：00到达B处，此时观测到灯塔P在其正西方向，若港口A与灯塔P的距离为40海里，求海轮的航行速度．（结果精确到1海里/时；参考数据： $s i n 20 ° \approx 0.34$ ， $c o s 20 ° \approx 0.94$ ， $t a n 20 ° \approx 0.36$ ）

查看试题解析
22. 为落实《教育部办公厅关于加强义务教育学校作业管理的通知》，进一步减轻中小学生的课业负担，规定中学生每天家庭作业时间少于1.5小时（90分钟），为符合作业管理要求，某校对该校七年级学生一周（7天）“家庭作业时间”（单位：小时）进行了随机抽样调查，并将获得的数据绘制成如下统计表，请根据表中的信息回答下列问题．
周家庭作业时间t（单位：小时）
频数
频率
$0 \leq t < 3.5$
5
0.05
$3.5 \leq t < 7$
20
0.20
$7 \leq t < 10.5$
m
0.35
$10.5 \leq t < 14$
25
n
$14 \leq t < 17.5$
15
0.15

(1)、统计表中m的值为， n的值为．

(2)、小丽同学说：“我的周家庭作业时间是此次抽样调查所得数据的中位数．”请直接写出小丽同学的周家庭作业时间在哪个范围内．

(3)、已知该校七年级学生有700人，试估计该校七年级学生每周“家庭作业时间”符合作业管理要求的人数．

查看试题解析
23. 涛涛同学骑共享单车保持匀速从家到博学书店买书，选好书付好款后，以相同的速度原路骑共享单车返回家中．设涛涛同学距离家的路程为 $y (m)$ ，运动时间为 $x (m i n)$ ， y与x之间的函数图象如图所示．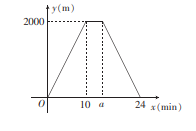

(1)、 $a =$ ．

(2)、在涛涛同学从书店返回家的过程中，求y与x之间的函数关系式．

(3)、在涛涛从家里出发的同时，小波同学以60m/min的速度从博学书店匀速步行去涛涛家，当小波同学与涛涛同学在路上相遇时，直接写出涛涛同学的运动时间．

查看试题解析
24. 如图，AB是 $⊙ O$ 的直径，点C在 $⊙ O$ 上（不与点A，B重合），连接AC，BC过点C作 $⊙ O$ 的切线交AB的延长线于点P，过点O作 $O E ∥ A C$ 交BC于点D，交PC于点E．

(1)、求证： $∠ P C B = ∠ P O E$ ．

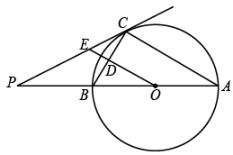(2)、若 $P B = \frac{1}{2} A B$ ， $A C = 12$ ，求DE的长．

查看试题解析
25. 在平面直角坐标系xOy中，已知抛物线 $y = a x^{2} - 4 a x + 3 a (a < 0)$ 与x轴分别交于A、B两点，且点A在点B的左侧．

(1)、求出点A、B的坐标．

(2)、记抛物线的顶点为C，连接AC，BC，当△ABC为等腰直角三角形时，在抛物线上是否存在一点D，使得 $∠ D O A = 45 °$ ？若存在，请直接写出点D的坐标；若不存在，请说明理由．

查看试题解析
26. 如图

(1)、问题提出：如图1，在△ABC中，D为BC上一点，且满足 $A D = B D = D C$ ，则△ABC形状为．（请填写序号：①钝角三角形；②直角三角形；③锐角三角形）

(2)、问题探究：如图2，四边形ABCD为 $⊙ O$ 的内接四边形， $∠ B A D = 60 °$ ， $∠ A B C = 90 °$ ，连接AC、BD，若 $B D = 6$ ，则对角线AC的长度为多少？

(3)、问题解决：如图3，在四边形ABCD中， $∠ A = ∠ C = 60 °$ ， $∠ A D C = 90 °$ ， $B C = C D$ ，以C为圆心，CB长为半径画 $\overset{⌢}{B D}$ ， M为 $\overset{⌢}{B D}$ 上的一动点，过点M作 $M E ⊥ A B$ ， $M F ⊥ A D$ ，连接EF．已知 $A D = 20$ ，探究：线段EF是否存在最小长度？若存在，请求出EF的最小长度；若不存在，请说明理由．

查看试题解析

周家庭作业时间t（单位：小时）	频数	频率
$0 \leq t < 3.5$	5	0.05
$3.5 \leq t < 7$	20	0.20
$7 \leq t < 10.5$	m	0.35
$10.5 \leq t < 14$	25	n
$14 \leq t < 17.5$	15	0.15