四川省成都市新都区2022年九年级下学期一诊考试数学试题
试卷更新日期:2022-04-26 类型:中考模拟
一、单选题
-
1. 在 , 0,1,-2四个数中,最小的数是( )A、 B、0 C、1 D、-22. 下列事件中,不是随机事件的是( ).A、打开电视,中央5套正在播放北京冬奥会赛事 B、“新冠”疫情将在2023年结束 C、抛掷一枚正方体骰子,出现点数7朝上 D、明天会下雨3. 2022年冬奥会在北京举行,以下历届冬奥会会徽是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 的算术平方根是( ).A、2 B、-2 C、±2 D、5. 60°角的正切值为( )A、 B、 C、 D、6. 在平面直角坐标系中,点关于原点对称的点的坐标是( )A、 B、 C、 D、7. 下列因式分解正确的是( )A、 B、 C、 D、8. 已知直角三角形的两边长分别为3和2,则第三边长为( )A、 B、 C、1 D、 或9. 《九章算术》中有这样一个题:今有甲乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?其意思为:今有甲乙二人,不如其钱包里有多少钱,若乙把其一半的钱给甲,则甲的数为50;而甲把其 的钱给乙,则乙的钱数也为50,问甲、乙各有多少钱?设甲的钱数为x,乙的钱数为y,则可建立方程组为( )A、 B、 C、 D、10. 如图,点在反比例函数的图象上,点在反比例函数的图象上,且轴, , 垂足为点 , 交轴于点 , 则的面积为( )
4. 的算术平方根是( ).A、2 B、-2 C、±2 D、5. 60°角的正切值为( )A、 B、 C、 D、6. 在平面直角坐标系中,点关于原点对称的点的坐标是( )A、 B、 C、 D、7. 下列因式分解正确的是( )A、 B、 C、 D、8. 已知直角三角形的两边长分别为3和2,则第三边长为( )A、 B、 C、1 D、 或9. 《九章算术》中有这样一个题:今有甲乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?其意思为:今有甲乙二人,不如其钱包里有多少钱,若乙把其一半的钱给甲,则甲的数为50;而甲把其 的钱给乙,则乙的钱数也为50,问甲、乙各有多少钱?设甲的钱数为x,乙的钱数为y,则可建立方程组为( )A、 B、 C、 D、10. 如图,点在反比例函数的图象上,点在反比例函数的图象上,且轴, , 垂足为点 , 交轴于点 , 则的面积为( ) A、4 B、5 C、6 D、7
A、4 B、5 C、6 D、7二、填空题
-
11. 二次根式中字母的取值范围是 .12. 将抛物线向左平移3个单位长度,再向上平移4个单位长度,得到的抛物线的函数表达式为 .13. 在一个不透明的布袋中装有18个白球和若干个黑球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,摸到白球的概率是 , 则黑球的个数为 .14. 如图,在中, , , 以点为圆心,以小于的长为半径作弧,分别交于点 , 交于点 , 再分别以点 , 为圆心,大于的长为半径作弧,两弧交于点 , 作射线交于点 , 连接 , 则 .
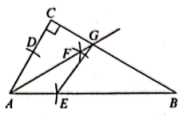 15. 估算:若 , 且 , 为连续的正整数,则 , .16. 如图所示,在中,已知 , , 点在边上,将绕点按顺时针旋转后,当点恰好落在初始的边所在直线上时,那么 .
15. 估算:若 , 且 , 为连续的正整数,则 , .16. 如图所示,在中,已知 , , 点在边上,将绕点按顺时针旋转后,当点恰好落在初始的边所在直线上时,那么 . 17. 如图所示,在一次数学活动课上,初三(1)班的同学们利用长杆来测量某段城墙的倾斜角 , 把一根长为6.6米的长杆斜靠在城墙旁,量出杆长2米处在地面投影的长约为1米,长杆的底端与墙角的距离约为2.7米,则倾斜角的正切值约为 . (结果精确到0.01,参考数据)
17. 如图所示,在一次数学活动课上,初三(1)班的同学们利用长杆来测量某段城墙的倾斜角 , 把一根长为6.6米的长杆斜靠在城墙旁,量出杆长2米处在地面投影的长约为1米,长杆的底端与墙角的距离约为2.7米,则倾斜角的正切值约为 . (结果精确到0.01,参考数据) 18. 在中, , , 是边上的中线,记且为正整数.则使关于的分式方程有正整数解的概率为 .19. 如图,抛物线与轴交于点 , 顶点坐标 , 与轴的交点在 , 之间(包含端点),则下列结论正确的有 . ①;②;③对于任意实数 , 恒成立;④关于的方程有两个不相等的实数根.(填编号)
18. 在中, , , 是边上的中线,记且为正整数.则使关于的分式方程有正整数解的概率为 .19. 如图,抛物线与轴交于点 , 顶点坐标 , 与轴的交点在 , 之间(包含端点),则下列结论正确的有 . ①;②;③对于任意实数 , 恒成立;④关于的方程有两个不相等的实数根.(填编号)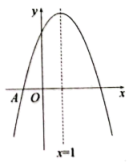
三、解答题
-
20.(1)、计算: .(2)、求不等式组的非负整数解.21. 先化简,再求值: , 其中 .22. 我区某学校根据《成都市中小学生课后服务实施意见》,积极开展课后延时服务活动,提供了“器乐,体锻,科创,书法,美术,课本剧,棋类……”等课程供学生自由选择,半学期后,该校为了解学生对课后延时服务的满意情况,随机对部分学生进行问卷调查,并将调查结果按照“A.满意;B.比较满意;C.基本满意;D.不满意”四个等级绘制成如图所示的两幅不完整统计图.

请根据图中信息,解答下列问题:
(1)、将条形统计图补充完整;(2)、表示等级C的扇形的圆心角是度;(3)、由于学校条件限制,“科创”课程仅剩下一个名额,而学生小华和小亮都想参加,他们决定采用抽纸牌的方法来确定,规则是:“将背面完全相同,正面分别标有数字1,2,3,4的四张牌洗匀后,背面朝上放置在桌面上,每人随机抽一次且一次只抽一张;一人抽后记下数字,将牌放回洗匀背面朝上放置在桌面上,再由另一人抽.若小华抽得的数字比小亮抽得的数字大,名额给小华,否则给小亮.”请用画树状图或列表的方法计算出小华和小亮获得该名额的概率,并说明这个规则对双方是否公平.23. 2022年冬季奥运会在北京举行,激起了人们对冰雪运动的极大热情.如图是某滑雪场高级雪道缆车线路示意图,滑雪者从点出发,途经点后到达终点 , 其中 , , 且段的运行路线与水平面的夹角为30°,段的运行路线与水平面的夹角为37°,求从点运行到点垂直上升的高度.(结果保留整数;参考数据: , , )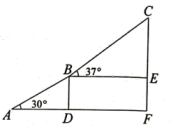 24. 如图,在平面直角坐标系中,一次函数与反比例函数的图象交于 , 两点,一次函数的图象与轴交于点 .
24. 如图,在平面直角坐标系中,一次函数与反比例函数的图象交于 , 两点,一次函数的图象与轴交于点 . (1)、求一次函数的解析式;(2)、根据函数的图象,直接写出不等式的解集;(3)、点是轴上一点,且的面积等于面积的2倍,求点的坐标.25. 已知四边形中, , 两点分别在 , 上,且满足 .
(1)、求一次函数的解析式;(2)、根据函数的图象,直接写出不等式的解集;(3)、点是轴上一点,且的面积等于面积的2倍,求点的坐标.25. 已知四边形中, , 两点分别在 , 上,且满足 . (1)、如图1,当四边形为正方形时,
(1)、如图1,当四边形为正方形时,①求证:;
②求证:;
(2)、如图2,当四边形为菱形时,若 , 试探究 , , 的数量关系.26. 为了更好应对突发疫情,某市政府积极储备防疫物资,将租用甲,乙两种货车共16辆,把医疗器材266吨,生活必需品169吨全部运到应急物资储备中心.已知一辆甲种货车同时可装医疗器材18吨,生活必需品10吨;一辆乙种货车同时可装医疗器材16吨,生活必需品11吨,设租用甲种货车辆.(1)、若将这批货物一次性运到应急物资储备中心,有哪几种租车方案;(2)、若甲种货车每辆需付燃油费1500元,乙种货车每辆需付燃油费1200元,设所付费用为元,求与的函数关系式,并求出哪种租车方案费用最少.27. 如图,和是有公共顶点的等腰直角三角形, , 把绕点旋转,点为射线与的交点. (1)、如图1,当点在线段上时,求证:;(2)、若 , ,
(1)、如图1,当点在线段上时,求证:;(2)、若 , ,①如图2,当点在延长线上时,求的长;
②在旋转过程中,当四边形为正方形时,直接写出线段长度的值.
28. 如图1,抛物线与轴交于 , 两点,与轴交于点 , , 点横坐标为2,延长矩形的边交抛物线于 . (1)、求抛物线的解析式;(2)、如图2,若点是直线上方的抛物线上的一个动点,过点作轴的垂线交直线于点 , 求的最大值;(3)、如图3,如果点是抛物线对称轴上一点,抛物线上是否存在点 , 使得以 , , , 为顶点的四边形是平行四边形?若存在,求出所有满足条件的点的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图2,若点是直线上方的抛物线上的一个动点,过点作轴的垂线交直线于点 , 求的最大值;(3)、如图3,如果点是抛物线对称轴上一点,抛物线上是否存在点 , 使得以 , , , 为顶点的四边形是平行四边形?若存在,求出所有满足条件的点的坐标;若不存在,请说明理由.