四川省广元市2022年中考数学模拟试题

试卷更新日期：2022-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 若有理数 $a$ ， $b$ ， $c$ 满足 $| a - b | = 2$ ， $| b - c | = 6$ ，则 $| a - c | =$ （）

A、6 B、8 C、4 D、4或8

查看试题解析
2. 下列几何图形中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、4a-a=3 B、2(2a-b)=4a-b C、(a+b)²=a²+b² D、(a+2)(a-2)=a²-4

查看试题解析
4. 一组数据：1、2、2、3，若添加一个数据2，则发生变化的统计量是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
5. 下列命题正确的是（）

A、对角线互相垂直的平行四边形是菱形 B、有一个角是直角的四边形是矩形 C、有一组对角相等的四边形是平行四边形 D、对角线互相垂直且相等的四边形是正方形

查看试题解析
6. 用三角板作 $△ A B C$ 的边 $A C$ 上的高，下列三角板的摆放位置正确的是（）

A、 B、 C、 D、

查看试题解析
7. 圆锥的底面半径为1，母线长为3，则该圆锥侧面积为（）

A、3 B、6π C、3π D、6

查看试题解析
8. 已知二次函数y=﹣x²+x+6及一次函数y=﹣x+m，将该二次函数在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新函数（如图所示），请你在图中画出这个新图象，当直线y=﹣x+m与新图象有4个交点时，m的取值范围是（）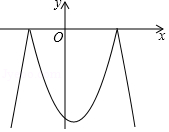

A、﹣ $\frac{25}{4}$ ＜m＜3 B、﹣ $\frac{25}{4}$ ＜m＜2 C、﹣2＜m＜3 D、﹣6＜m＜﹣2

查看试题解析
9. 如图，正方形的四个顶点在半径为 2 的大圆圆周上，四条边都与小圆都相切， $A B ， C D$ 过圆心 $O$ ，且 $A B ⊥ C D$ ，则图中阴影部分的面积是（）

A、 $4 π$ B、 $2 π$ C、 $π$ D、 $\frac{π}{2}$

查看试题解析
10. 如图所示，△ACB中，∠ACB＝90°，CD⊥AB于D，则下列结论：①BC＞CD；②AC＞AD；③AB＞AC；④BC＞AD．正确的有（）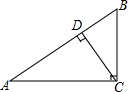

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 计算： $\sqrt{5776}$ ＝．

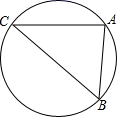
查看试题解析
12. 已知点A在数轴上，且和表示1的点相距 $\sqrt{3}$ 个单位长度，则点A表示的数为．

查看试题解析
13. 如图，点A，B，C在同一个圆上，∠ACB＜90°，弦AB的长度等于该圆半径的 $\sqrt{2}$ 倍，则cos∠ACB的值是.

查看试题解析
14. 如图，在△ABC中，AB＝AC，点A在y轴上，点C在x轴上，BC⊥x轴，tan∠ACO＝ $\frac{2}{3}$ ．延长AC到点D，过点D作DE⊥x轴于点G，且DG＝GE，连接CE，反比例函数y＝ $\frac{k}{x}$ （k≠0）的图象经过点B，和CE交于点F，且CF：FE＝2：1．若△ABE面积为6，则点D的坐标为．

查看试题解析
15. 如图，直线 $l$ 过正方形 $A B C D$ 的顶点 $B$ ，点 $A ， C$ 到直线 $l$ 的距离分别是 $a$ 和 $b$ ，且满足： $\sqrt{a - 1} + | b - 2 | = 0$ ，则正方形 $A B C D$ 的面积是．

查看试题解析

三、解答题

16. 解方程： $\frac{3 x - 2}{5} + 2 = - \frac{x + 6}{5}$

查看试题解析
17. 先化简，再求值：（1 $- \frac{2}{x + 1}$ ） $\div \frac{x^{2} - 1}{2 x + 2}$ ，其中x $= \sqrt{2} -$ 1．

查看试题解析
18. 如图，在平行四边形ABCD中，连接对角线AC，延长AB至E，使BE＝AB，连接DE，分别交BC，AC于点F，G．

(1)、求证：BF＝CF；

(2)、若BC＝6，DG＝4，求FG的长；

(3)、若△FCG面积为1，则四边形ABFG面积为多少？

查看试题解析
19. 某汽车配件厂生产甲、乙、丙三种汽车轮胎．生产各种轮胎所需的工时和产值如下表所示，又知道每周生产三种轮胎的总工时是168个，总产值是111.2万元
汽车零部件
甲种
乙种
丙种
每个所需工时（个）
$\frac{1}{2}$
$\frac{1}{3}$
$\frac{1}{4}$
每个产值（千元）
4
3
1

(1)、若每周丙种轮胎生产252台，问其它两种轮胎每周分别生产多少个？

(2)、现有4S店以产值价的1.2倍购进这三种轮胎共100个，考虑市场需求和资金周转，其中丙种轮胎购进50个，而用于购买这100个轮胎的总资金最少24.96万元，但最多不超过25.2万元，那么该商店有哪几种购进轮胎方案？

(3)、若销售每件甲种轮胎可获利200元，每件乙种轮胎可获利150元，每件丙种轮胎可获利100元，在第（2）问的进货方案中，哪一种方案获利最大？最大利润是多少元？

查看试题解析

20. 在初三年级某班的一次体育模拟测试中，班长对全班同学的测试成绩进行了统计，并绘制了如下不完整的统计图表，请根据图表提供的信息完成以下问题：

组别	成绩	人数
A	90≤x<100	4
B	80≤x<90	15
C	70≤x<80	m
D	60≤x<70	10

(1)、图表中：m＝；B组的圆心角为度．

(2)、A组4名同学中有2男2女，从中随机抽取两名同学参加市运会，请你用画树状图或列表法求：

①被抽取的2名同学恰好是1男1女的概率；

②至少1名男生被抽到的概率．

查看试题解析

21. 2019年12月27日，我国成功发射了“长征五号”遥三运载火箭.如图，“长征五号”运载火箭从地面 $A$ 处垂直向上发射，当火箭到达 $B$ 处时，从位于地面 $M$ 处的雷达站测得此时仰角 $∠ A M B = 45 °$ ，当火箭继续升空到达 $C$ 处时，从位于地面 $N$ 处的雷达站测得此时仰角 $∠ A N C = 3 0^{∘}$ ，已知 $M N = 120 k m$ ， $B C = 40 k m$ .

(1)、求 $A B$ 的长；

(2)、若“长征五号”运载火箭在 $C$ 处进行“程序转弯”，且 $∠ A C D = 10 5^{∘}$ ，求雷达站 $N$ 到其正上方点 $D$ 的距离.

查看试题解析
22. 点A（﹣3，1），B（﹣2，2），反比例函数y＝ $\frac{k}{x}$ （k＜0，x＜0）的图象记为L ．

(1)、若L经过点A ．
①图象L的解析式为 ▲ ．

②点B在图象L上，还是在图象L的上方或下方？为什么？

(2)、如图在（1）的条件下，L上纵坐标为3的点P与点C关于原点O对称，PQ⊥x轴于点Q ， CD⊥x轴于点D ．求△QCD的面积．

(3)、若L与线段AB有公共点，直接写出k的取值范围．

查看试题解析
23. 已知：如图所示，MN是⊙O的直径，B是⊙O上一点，NP平分∠BNM交⊙O于P，过P作PA⊥BN于A．

(1)、求证：PA与⊙O相切；

(2)、若MN＝20，BN＝12，求MP的长；

(3)、若D是ON中点，过D作CD⊥ON交AP于C，若CD＝19，tan∠MNP＝ $\frac{3}{4}$ ，求⊙O的半径．

查看试题解析
24. 从三角形（不是等腰三角形）一个顶点引出的一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形有两角对应相等，我们把这条线段叫做这个三角形的“优美分割线”.

(1)、如图，在△ABC中，CD为角平分线，∠A＝40°，∠B＝60°，求证：CD为△ABC的“优美分割线”.

(2)、在△ABC中，∠A＝46°，CD为△ABC的“优美分割线”且△ACD为等腰三角形，求∠ACB的度数.

(3)、在△ABC中，∠A＝30°，AC＝6，CD为△ABC的“优美分割线”，且△ACD是等腰三角形，求线段BD的长.

查看试题解析
25. 如图1，在平面直角坐标系xOy中，直线l：y＝ $\frac{1}{2}$ x+m与x轴、y轴分别交于点A和点B（0，﹣1），抛物线y＝ $\frac{1}{2}$ x²+bx+c经过点B，且与直线l的另一个交点为C（4，n）．

(1)、求n的值和抛物线的解析式；

(2)、点D在抛物线上，且点D的横坐标为t（0＜t＜4）．DE∥y轴交直线l于点E，点F在直线l上，且四边形DFEG为矩形（如图2），点H是直线BC上横坐标为﹣3的点．
①若矩形DFEG的周长为p，求p与t的函数关系式以及p的最大值；

②在p取最大值时，有一动点Q从点H出发，以每秒v个单位的速度沿射线HB运动到I点，然后以每秒 $\frac{2 \sqrt{5}}{5}$ v个单位的速度从点I运动到点D，若要点Q所用时间最少直接写出点I的坐标；

(3)、把直线BC绕着点A逆时针旋转45°，得到直线l′，点M是位于x轴上方的直线l′上的一动点，是否存在点M，使∠OMA＝∠ABO？若存在，请求出M点坐标：如果不存在，请说明理由．

查看试题解析

汽车零部件	甲种	乙种	丙种
每个所需工时（个）	$\frac{1}{2}$	$\frac{1}{3}$	$\frac{1}{4}$
每个产值（千元）	4	3	1